Design Patterns for Data Structures
Dung ("Zung") Nguyen
Department of Mathematics/Computer Science
Pepperdine University
Malibu, CA 90263
dnguyen@pepperdine.edu
Synopsis
Design patterns provide ways to structure software components into systems that are flexible, extensible, and have a high degree of reusability. The state pattern, the null object pattern, and the singleton pattern are used to implement common data structures such as lists and trees. These patterns help narrow the gap between the abstract views of the data structures and their concrete implementations. The smaller the gap, the higher the level of abstraction. The more abstract, the less complex the coding structure. As a result, algorithms are easier to understand and more manageable. This paper advocates teaching the above design patterns in data structures courses.
Seasoned software developers do not write programs from scratch. They always look for patterns that best match the context of the problem they are trying to solve, and apply them to designing their software. Design patterns are design solutions to recurring problems in software construction. The authors of Design Patterns [3] assign names to the most used and proven patterns, and catalog them. Design patterns are often misconstrued as applicable only to programming in the large. In reality, they can be applied to solving problems in programming in the small such as implementing data structures. We assume the reader is familiar with the concepts of object-orientation and data structures. Perhaps less well known are the design patterns. Their usefulness and their relevance are most apparent when they are presented in the context of design problems and the solutions they offer.
When we teach data structures, we first describe their abstract specifications, and then proceed to show how to implement them. Abstraction is the computer scientist’s tool to master complexity. The more closely the implementations map to the abstract views of the data structures, the more elegant and flexible the implementations will be. This paper describes how object-oriented design patterns shape our thinking and aid us in designing data representations to the degree of abstraction we desire. By focusing on common data structures such as lists and trees, it illustrates how these patterns help narrow the gap between the abstract views of the data structures and their concrete implementations. The patterns also help exploit polymorphism in an effective way and keep control structures to a minimum. Code complexity is reduced, and the overall complexity of the system becomes more manageable.
Section 2 examines lists and trees and views them as special cases of container classes. They are systems of objects that have states and that can change states dynamically. The key is to encapsulate the states of a system as classes. This calls for the state pattern. Section 3 describes in some details the state pattern and the null-object pattern, and applies them to partially implement the linked list structure. The null-object pattern is used to represent the empty state. The system behaves differently in different states, as if it changes classes dynamically. The state pattern provides a flexible and elegant way to implement this behavior. Section 4 completes the design of lists and trees by incorporating the singleton pattern with the state pattern. Conceptually, there is only one empty state. The singleton pattern will ensure the uniqueness of the empty state, and allow it to be shared by all data structures of the same class. Section 5 concludes with a brief description of other design patterns that can be applied to other data structures such as stacks and queues.
We have implemented all the above data structures in Java. We use the Unified Modeling Language (UML) notation to represent all class and state diagrams. However, due to space restriction, we will be able to exhibit only a few code samples and a few class diagrams. Interested readers can obtain our complete set of code and diagrams by sending e-mail to the address listed in the author information above.
In programming, it is often necessary to have objects with which one can store data, retrieve data when needed, and remove data when no longer needed. Such objects are instances of what we call container classes. A container class is an abstraction defined by three methods: insert, remove, and retrieve. In Java, this abstraction can be represented in the form of an interface as shown in Listing 1 below.
package containers;
public interface IContainer
{
Object retrieve (Object key);
/*
Post: If there is an object associated with key then this object is returned else null is returned.*/
Object remove (Object key);
/*
Post: retrieve (key) returns null, and if there is an object associated with key then this object is returned else null is returned.*/
void insert (Object key, Object value);
/*
Post: The pair (key, value) is stored in this container with no duplication and in such a way that retrieve (key) returns value.*/
}
Listing 1: Container Interface.
It is by no coincidence that the post-conditions for the insert and the remove methods involve the retrieve method. When the insert or remove method is carried out, the state of the container object changes and dictates what the retrieve method should return. The interrelationship between methods of a class occurs quite frequently.
There are basically two schemes for organizing the objects for storage: a linear scheme and a non-linear scheme. This leads to the notion of container structures. The linear container structure is called a list. The non-linear structure can be sub-classified into many sub-types such as the various tree structures and hash tables. Container structures are abstract. For example, the list structure, or list for short, is defined as follow.
A list is a container that can be empty or not empty. If a list is empty, it contains no data object. If is not empty, it contains a data object called the head, and a list object called the tail.
The abstract definition of a non-linear structure such as the binary search tree structure, or binary search tree for short, is similar though somewhat more involved, as in the following.
A binary search tree (BST) is a container that can be empty or not empty. The objects it contains are totally ordered according to a relation called "is less than". If a BST is empty, it contains no data object. If a BST is not empty, it contains a data object called the root, and two distinct binary search trees called the left and the right subtrees. All the elements in the left subtree are less than the root, and the root is less than all the elements in the right subtree.
Container structures such as the above lists and trees can be implemented using arrays or dynamic memory allocation. The list implementation using dynamic memory is usually called a linked list. In this paper, we focus only on dynamic memory allocation. Most implementations in this case use the null pointer to represent the empty structure. Because the semantics of a null pointer is too low-level to adequately encapsulate the behavior of an object, such implementations have a high degree of code complexity, and are cumbersome to use. A null pointer (or a null reference in Java) has no behavior and thus cannot map well to the mathematical concept of the empty set, which is an object that exists and that has behavior. We seek to narrow the gap between the conceptual view of a container structure and its implementation. In our convention, the null pointer is to represent the non-existence of an object only. Emptiness and non-emptiness are simply states of a container structure. The key here is to encapsulate states as classes. This is the gist of a well-known design pattern called the state pattern [3].
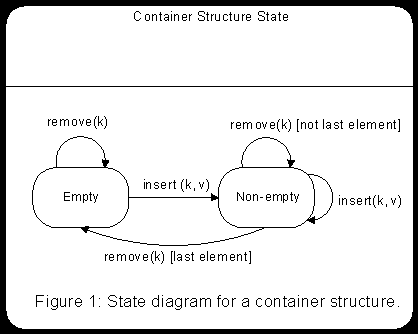
A container structure is a system that may change its state from empty to non-empty, and vice-versa. For example, an empty container changes its state to non-empty after insertion of an object; and when the last element of a container is removed, its changes its state to empty. Figure 1 below diagrams the state transition of a container structure.

For each distinct state, the algorithms to implement the methods differ. For example, the algorithm for the retrieve method is trivial in the empty state -it simply returns null- while it is more complicated in the non-empty state. The system thus behaves as if it changes classes dynamically. This phenomenon is called "dynamic reclassification." The state pattern is a design solution for languages that do not support dynamic reclassification directly. This pattern can be summarized as follow.
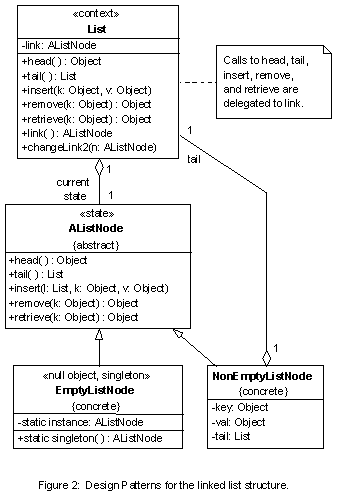
Application of the state pattern to designing a linked list class is straightforward. We name this class, List, and the abstract class for list states, AListNode (as in abstract list node). AListNode has two concrete subclasses: EmptyListNode, and NonEmptyListNode. The EmptyListNode has no data while the NonEmptyListNode contains a data object, and a tail, which is a List. One can see how closely this implementation maps to the following portion of the abstract definition of a list: If a list is empty, it contains no data object. If is not empty, it contains a data object called the head, and a list object called the tail. The class List contains an instance of a concrete subclass of AListNode. Via polymorphism, it can be an EmptyListNode or a NonEmptyListNode at run time. In order to qualify it as a container class, we add to the behavior of class List the three container methods: insert, remove, and retrieve. This design closely reflects the first portion of the abstract list definition: A list is a container that can be empty or not empty. Listing 2 below shows the implementation of the state design pattern for linked lists in Java. Due to space restriction, we only show the code for insert
.
package containers;
public class List implements IContainer
{
private AListNode _link; //state.
AListNode link () {
//
Visible only to package.return _link;
}
void changeLink2 (AListNode n) {
//
Change state; visible only to package._link = n;
}
public List (){
//
Post: this List exists and is empty.//
constructor code goes here…}
public void insert (Object key, Object v) {
//
Pre : key and v are not null._link.insert (this, key, v);
}
//***O
ther constructors and methods...}
abstract class AListNode {
//
Visible only to package.abstract
void insert (List l, Object k, Object v);
//
Pre : l, k and v are not null.
//***O
ther abstract methods...}
class NonEmptyListNode extends AListNode {
//
Visible only to package.private Object _key;
private Object _val;
private List _tail;
NonEmptyListNode (Object k, Object v) {
//
Pre : k and v are not null.//
Post: this node exists and contains k, v, and an empty tail._key = k;
_val = v;
_tail = new List ();
}
void insert (List l, Object k, Object v) {
if (k.equals (_key)) {
_val = v;
}
else {
_tail.insert (k, v);
}
}
//***
Other methods…}
class EmptyListNode extends AListNode {
//
Visible only to package.void insert (List l, Object k, Object v) {
l.changeLink2 (new NonEmptyListNode (k, v);
}
//***
Other attributes and methods…}
Listing 2:
State Design Pattern for Linked Lists.
The state design pattern, as illustrated in Listing 2 above, puts polymorphism to use an effective way. It distributes the complexity of the algorithms for insert and remove over two disjoint concrete subclasses of AListNode. Polymorphism via the abstract state class will dynamically select the appropriate method of the appropriate concrete subclass to execute. The programmer need not write conditional statements to check on the state of the system for each method invocation. As a result, the algorithms in each of the subclasses have minimal control structure, and are easier to understand. The code complexity of the algorithm is reduced and becomes much more manageable.
In Listing 2, the classes List, AListNode, EmptyListNode, and NonEmptyListNode belong to package containers. Clients of this package can only access List and need not and should not know anything about the node classes. Information hiding implemented as such, protects the clients from any accidental misuse of the class List. It also shields the clients from any unforeseen modification of the non-public classes in the package. Clients invoke the constructor List () to create as many empty lists as needed. The notion of emptiness is embodied in the mathematical concept of the empty set. The emptiness of a list is represented not by a null pointer, but by an EmptyListNode object. Ideally, this EmptyListNode object should be unique and shared by all empty List objects. The singleton pattern provides a design solution to this problem. The following code fragment for class EmptyListNode illustrates how the singleton pattern is implemented.
class EmptyListNode extends AlistNode {
private static AListNode _unique = null;
static AListNode singleton () {
if (null == _unique)
_unique = new EmptyListNode ();
return _unique;
}
//***
Other attributes and methods…}
Class List is a client of this singleton. Its constructor
List simply calls the class method EmptyListNode.singleton to initialize itself to the empty state, as shown in the following code fragment.
public List () {
_link = EmptyListNode.singleton ();
}
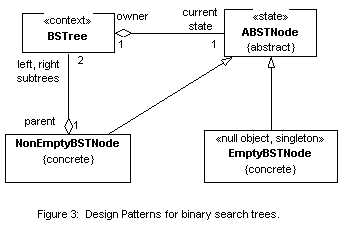
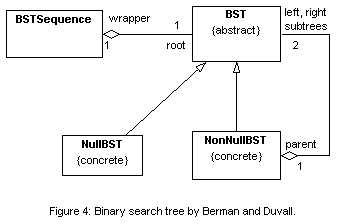
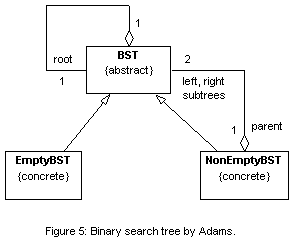
The design of the linked list structure is now complete. Its class diagram is shown in Figure 2 below. With a slight and trivial modification, it can be reused to implement tree structures. Figure 3 shows the class diagram for the binary search tree. There is not enough space here to exhibit the code and discuss how code complexity is reduced. Figures 4 and 5 are the designs of the binary search tree by Berman and Duvall [2], and by Adams [1], respectively. These designs do not use the patterns described in this paper. Unfortunately, space limitations do not allow a comparative discussion between the various implementations.
Many other design patterns have application in data structures. The above design for binary search trees can be extended to implement balanced tree structures as well: a tree can be in a balanced or an unbalanced state. The iterator pattern hides the details in traversing container structures. The strategy pattern decouples a queue from its queueing policy. A stack is simply a queue with a last-in-first-out queueing policy. The adapter pattern converts the interface of a queue to that of a stack.
The authors of Design Patterns write: "Designing object-oriented software is hard, and designing reusable object-oriented software is even harder." Taken out of context, this statement appears highly negative. In reality, it serves as the main source of motivation for the authors to write a book on design patterns to help remedy the situation. If object-oriented programming is hard, teaching it is at least as hard. By introducing design patterns on a smaller scale such as using them in implementing data structures, we can teach students solid object-oriented designs and sound software engineering principles early, and help prepare them for careers in computing.