Abstraction is the process by which we factor out some complex subset of "experience" and give it a name. The name then serves as a surrogate for the complexity of the experience. The name itself, as it is used, becomes a part of the complexity of our experience and thus serves as the basis for further abstractions. This book is about abstraction. Humanity has progressed from a primitive state primarily because of the ability to form and use abstractions and to build ever more complex abstractions "on the backs" of simpler ones. Concepts that we use every day in the business world (corporation, loan, credit, etc.) are very abstract, based on simpler abstractions (association, value, etc.), and yet we normally think of them as quite "concrete."
Not only is abstraction useful to us, it is absolutely necessary. Psychologists have determined that the human mind (of most of us, at least) is limited by what I will call the "Rule of Seven"(Miller,G.A., The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychological Review, 1956, v63, pp. 81-96). According to this rule, we are capable of simultaneously manipulating about seven independent items in our minds. For example, we may drive an automobile, listen to music, talk to the person next to us, and keep generally aware of what our friends are up to in the back seat, all simultaneously. A person learning to drive a car, however, has a much harder time integrating the various tasks needed to manipulate the controls, thinking of each of them as distinct. Each of us will eventually reach a point where we cannot add more tasks without reaching overload. Experiments suggest that overload is reached by most people when the number of independent tasks is about seven. A simple demonstration of this is that it is easier to remember telephone numbers (seven digits) than social security numbers (nine digits). Once we reach the point of overload, we need some organizational or abstraction aid to help us deal with the complexity. For example, I remember my own SSN as a sequence of three smaller numbers rather than as one long number. The hyphens normally written in the SSN seem to be a real help in remembering the number. As an experiment of your own, think about how many telephone numbers you mentally carry around, versus how many social security numbers you think you would be able to remember.
The limitation of the Rule of Seven is overcome by our ability to form abstractions. The ability to factor out some complexity (several independent items) and let it be represented by an abstraction or surrogate (a single item) automatically reduces the tendency to overload and lets us use our mental power to the maximum.
More specifically the book is about how a programmer may use object oriented programming techniques to build software which is maximally reusable by applying principles of abstraction. Programmers have wanted to build reusable software components almost from the beginning. The first (and nearly only successful) attempt was the FORTRAN Library, which contained numerical routines such as SIN and LOG, which freed most programmers from the need to program such subroutines in order to use them. The fact that they were widely implemented and fairly true to an abstract model of behavior increased the portability of programs which used them. Portability, the ability to move software easily from one machine to another, is only one of the goals of reusable software however. Another is the ability to reuse components of one project in others. In nearly every field of human action one hears the admonition "Don't reinvent the wheel" whenever attempts are made to advance the state of the art. In programming however it is still too often true that components are rebuilt from scratch for each new use. This contrasts sharply with the general practice in hardware design of using standardized, off the shelf, components to build much of a new hardware system. The same can and should be true of software.
Object oriented programming offers hope of being able to provide a mechanism by which software components may be more easily reused, extended, and especially, interchanged among practitioners. Smalltalk is a small and simple language developed by Xerox in the 70's and 80's. It is always furnished with a large and complex software library called the "class hierarchy." The Smalltalk class hierarchy has proven to provide a mechanism of reusability and extendibility over a number of years on large and small projects . A person programs in Smalltalk by exploiting the power of the class library more than the power of the language itself. There is a negative aspect to Smalltalk however, if one is to build large, multi-person/year software systems. The class library is on line in source form and easily modified. This advantage for prototyping is a disadvantage for large systems where there is more need of stable specifications as a means of communication among the various people building the system.
Modula-3 offers some advantages, especially to the person learning about how to build large, reliable software systems. It is strongly typed, providing early warning of potential errors. It has a definite modularity, permitting separate compilation of modules. It has good information hiding, making it easier to control change. It is also highly object-oriented, which, as we shall see, offers definite advantages when we require large, modular programs.
Object oriented programming (OOP) began with the language Simula, developed in Scandinavia in the mid 60's. Simula was used primarily for simulation programming, where it is natural to model external entities in the software system, and to think in terms of the entities and their behavior. Simula has a syntax much like that of Pascal (which was created at about the same time, and in the same tradition), but the practitioner thinks quite differently when designing a program that will be built in Simula. Rather than deciding on the various processes that must be implemented to complete the system, the designer thinks in terms of the entities (objects) which do exist in the system being modeled, and how they will be represented in the model. The designer then thinks about whether the objects are unique in the system, or whether several objects of the same kind will exist. These collections of similar objects are called "classes", and the chief job of the designer is to design the classes. Objects within a class have the same behavior, so the primary job in designing a class is to determine the behavior of the objects in the class. Often these behaviors are interactions with objects of the same or other classes, so communication patterns must be established to model the interactions. These communication patterns result in objects sharing information by sending messages to each other. One object requests a service from another by sending it a message. The receiving object executes some procedure to provide the service to the sender.
A fundamental idea of OOP, introduced in Simula, is that of inheritance. Using inheritance, a programmer describes a class by extending or specializing some existing class. The description of the new class is only a description of the differences between the old and the new classes. New behaviors can be added and old ones can be modified. There are two benefits of this. The first, though less important, is that it eases the programmers task if much of the behavior of a new kind of object is already programmed into the system. More importantly, classes organized by inheritance into a class hierarchy constitute a unifying structure around which a software system may be built and understood (as per Rule of Seven) by its designers, programmers and users. In effect each class forms an abstraction on which other abstractions may be built.
In brief, the main difference in programming in the object oriented style is that the design of the data items (objects within classes) comes before the design of the procedures (behaviors of the objects, called "methods" in OOP).
After Simula, the next generally known language to adopt support for object oriented programming was Smalltalk, developed in the 70's at XEROX PARC (Palo Alto Research Center). The design of the language was driven by the desire to provide a rapid prototyping system on powerful, personal workstations. It was developed as an aid in the design of graphical human-computer interface systems, and was originally an experiment. Smalltalk and the systems built with it, while not wildly successful in the marketplace (in fact it was purposely kept out of the marketplace for years) have been responsible for much of the evolution in desk top systems that has led to the Macintosh and to OS/2.
Both Simula and Smalltalk are elegantly designed, offering a small number of powerful concepts, and a purity or uniformity that makes them easy to learn, relative to the complexity of the things that may be done with them. Smalltalk does have a reputation for being difficult to learn, but this is due to the richness of the library of source code which is provided with each system, and which must be learned to make full use of the language.
Object Pascal was developed at Apple Computer in the early 80's to add support for OOP to a popular and fairly standardized version of Pascal: UCSD Pascal. The language was designed by a team headed by Larry Tesler (formerly of XEROX PARC, and a developer of Smalltalk) and aided by Niklaus Wirth (the developer of Pascal). UCSD Pascal (from the University of California at San Diego) already had a modular structure, permitting separate compilation of modules (called units) and separation of interface and implementation. Rather than creating a language from the ground up, Object Pascal was to be an extension of Pascal. The only changes were those necessary to permit the creation of a class hierarchy, to create classes, and to implement the message passing method of procedure execution that appears in Smalltalk and Simula. Even here the syntax changes were simple extensions of constructs already in the language, primarily the record structure. This makes it very easy to get started for those who know Pascal, as the syntax is very familiar. It is only necessary to learn the OOP style of programming, which, admittedly, may be wrenching for a while. The negative side is that Object Pascal lacks the uniformity of some other languages. Integers aren't objects for example, and occasionally you would like them to behave as objects. Sometimes you have to do some extra work to overcome the lack of uniformity. A conscious effort was made to keep the number of new concepts in Object Pascal as small as possible without overly affecting the power of the language, so this is not a great problem. Also on the negative side is the problem that most current implementations of Object Pascal have in hiding information that should not be seen and used by programmers, but which needs to be seen by compilers. Object Pascal is one of the primary development languages on the Macintosh and was originally used to develop MacApp, the standard application development environment. MacApp has now been rewritten in C++. The American National Standards Organization (ANSI) recently wrote a report on object oriented extensions to Pascal, based on the current standard "Extended Pascal". C++, developed in the 1980's at Bell Labs by Barjne Stroustrup, has become emensely popular recently by virtue of its support for object-oriented programming and its improved abstraction facilities over its predecessor, the C language. It is also being standardized by ANSI. Early versions of the language were relatively simple extensions of C. Today, C++ is probably the most widely used "object-oriented" language, though much of the code written in the language is not particularly object-oriented, as least not by the definition given later in this book. More properly, C++ can be described as a language that is optimized for data abstraction and information hiding, in which it is possible to program in an object-oriented style. This author has a book, similar to this one, that attempts to teach such a style in C++.
The object oriented paradigm has been successfully applied to functional programming with several extensions to Lisp and Scheme. In particular the Common Lisp Object System (CLOS) has been used to build several commercial systems. One of the advantages of the Lisp family of languages is that it is possible to add something as sophisticated as object oriented programming to the language without actually changing or extending the language. This is due to the great flexibility of Lisp.
In addition there are a number of other languages that support object oriented programming very well. Some of the best of these are Eiffel, Trellis/Owl, and Beta. Each of these is languages is suitable for the construction of large, complex software systems.
In the middle 80's a team composed of people from Digital Equipment's Systems Research Center in Palo Alto and Olivetti Corporation undertook the development of a new language that was to be used both in research and in systems development. The language report was first published in 1988 and has been revised once [Modula-3 Report...]. The language was to be a successor to Modula-2, though not, precisely, an extension. Nicklaus Wirth, developer of Pascal and Modula-2, participated in the effort, mostly by simplifying the proposals as they were developed. The final language is approximately as complex as Pascal, but is much more powerful. The simplicity was achieved by providing uniform rules, without exceptions, as well as a small number of very powerful features that cover the necessary techniques without overlapping. A number of language features were left to libraries, which provided additional simplification of the core language. For example, input and output, is handled through libraries, rather than in the language proper. This is the same approach taken by C and C++. In a few other areas, the language provides core functionality that is supplemented by the libraries. Thus TEXT is a built in type (character strings), but most functionality is provided by a library interface Text.i3.
A language is only a tool and not a panacea. Any language has advantages and disadvantages. Any language provides better support in some areas than in others. It is often useful to look at what application areas the designers of a language were interested in when you are trying to match a language to a software project. Even those languages that try to be all things to all programmers have their drawbacks, usually size and complexity. Programming in Modula-3, like in any language, is easier if the programmer adopts a mental attitude appropriate for the language, and adopts a style which complements the language and mitigates the weaknesses. This book will attempt to develop such a mental attitude and teach such a style.
Modula-3 is a powerful tool and a very complex language. Learning to use it well will empower the programmer. This is true in several ways, but the most important is the following. Given facility with powerful tools, especially organizational tools, and ideas, it becomes easier to use all tools, even simpler ones. The reverse is not true. Thus it is worth learning to program in the object oriented way, even if you have to program ultimately in languages offering no support whatever for OOP, as you will have learned additional important ways to organize software components that will make the task easier and the product more reliable.
Modula-3 contains a subset that is similar to, though not exactly the same as, Modula-2. Simple programs look very much like Pascal programs. In this section we will present some of the low level details that a programmer needs to know to be able to read Modula-3 effectively. We assume here that the reader is a "skilled novice" in either C or Pascal. This means that the reader is fluent with her or his language in terms of the usage of functions and procedures, arrays, program control statements, structs-records, and has had some experience programming with pointers. Appendix A has some additional material, especially on pointers. A more complete source of this information may be found in the book "Modula-3," by Sam Harbison. [Prentice-Hall, 1992]. A more complete source is the so-called Green Book, "Systems Programming with Modula-3" Greg Nelson, Editor, Prentice-Hall, 1991. Here we are going to focus on a few topics that we will need in this book. Some of them are quite elementary and some are not. We won't give the last word on any of them.
Modula-3 programs are built from Modules. Each Module consists of an interface part, stored in a file with file suffix ".i3," and an implementation part, stored in a file with suffix ".m3." The system provides an interface "Main.i3" and the main part of a Modula 3 program is an implementation of this interface. For example, the following is the traditional "Hello World" program written in Modula-3. Note that Module-3 is "case sensitive." Capitalization is important and must be consistent.
MODULE Main;
IMPORT Wr, Stdio;
BEGIN
Wr.PutText(Stdio.stdout, "Hello World.\n");
END Main.
The keywords, MODULE, IMPORT, BEGIN, END, are all in capitals. The end of the module repeats the name of the module. The import clause indicates that we want to utilize the features defined in Wr.i3, the write stream interface, and Stdio.i3, the standard input and output file interface. The Wr interface defines a function PutText that is used for writing strings (TEXTs) to streams. Stdio.stdout is the standard redirectable output stream, usually your terminal or workstation screen. "Hello World." is a text, but we have also included a "newline" character at the end of it so that the cursor will move to the beginning of the next line. The Wr and Stdio interfaces are provided with every Modula-3 system. Programmers may also write their own interfaces and import them into their Main programs.
The Modula-3 system is more complex that most other systems. The compiler has a very large number of options and it must coordinate properly with its linker. Because of this, the compiler and linker are seldom used separately. Instead, programmers use a system level tool called m3build. This program reads a description of our program from a file named m3makefile and it produces an executable file from the description and the source files. The standard way to use Modula-3 is to create a directory with the name of our project, say "hello" and to include in it a sub-directory named src (which you can read "sources," but it is also the initials of the Digital Equipment Corp. Systems Research Center, which maintains Modula-3). Include all of your source programs, here just Main.m3, in the src directory. Include the following m3makefile in the src directory as well. Then set your current directory to hello, the parent of src, and enter the m3build command. Everything else is automated. The m3makefile for our "Hello World" program follows.
implementation (Main)
import (libm3)
program (Hello)
This file tells m3build to look in Main.m3 for an implementation. It will be compiled. We also indicate that the Modula-3 library is needed. This gets us the standard interfaces like Wr and Stdio. Finally we say that the executable should be named Hello. The object and symbol files that result from compilations and the executable file will be created in a new subdirectory of hello that is named for your system architecture. If you are using linux, it will be named linux. If you have a DEC workstation 3100 it will be DS3100, etc. We will show a few, more sophisticated, m3makefiles later.
Modula-3 does all of its output using "streams." These are defined in a collection of standard interfaces. If our program or module is to do I/O we will want to IMPORT Rd.i3 or Wr.i3 or both (and include libm3 in our m3makefile, of course).
IMPORT Wr, Rd;
Wr.i3 allows us to create writers, and Rd.i3 permits creation of readers. A reader is like a faucet of input data. You turn it on and data comes into your variables. A writer is a sink of outputs. If we need to read and write from files we can importe FileStream.i3 to associate files with readers and writers. We can also use FileName.i3 to manipulate file and directory names. Finally Stdio defines Stdin, Stdout, and Stderr, the standard input (keyboard), output (screen) and error (screen) files. If our output needs to be formatted in any way, you can utilize the Fmt.i3 interface. In particular, Wr has procedures for outputting texts (Wr.PutText) and characters (Wr.PutChar), but not integers. If you want to write an integer you must first format it to a TEXT. The following program says hello to three worlds.
MODULE Main;
IMPORT Wr, Stdio, Fmt;
BEGIN
FOR i := 1 TO 3 DO
Wr.PutText(Stdio.stdout, "Hello World ");
Wr.PutText(Stdio.stdout, Fmt.Int(i));
Wr.PutChar(Stdio.stdout, `\n');
END;
END Main.
Note that the system interfaces, like Fmt.i3, are well documented. When in doubt, don't hesitate to read them. Look in directory usr/local/lib/m3/pkg/libm3/src.
Likewise, when doing input you will want to use the Scan.i3 interface to transform the texts input from a reader into typed data values such as integers.
The low-level data types available to the Modula-3 programmer are as follows, with examples of many of them.
Types Examples
INTEGER 48, -53
CARDINAL 0, 34358192
REAL 4.2, 8.0, 2.3E-6
LONGREAL
EXTENDED
TEXT "Hello World."
CHAR c', '\n'
BOOLEAN TRUE, FALSE
MUTEX
enumerations {North, East, South, West}
subranges [1..10], [North..South]
sets SET OF {North, East, South, West}
arrays ARRAY [1..10] OF INTEGER
records RECORD x,y:REAL END
pointers REF INTEGER
packed types BITS 4 FOR [1..10]
procedures PROCEDURE(i:INTEGER):INTEGER
objects OBJECT x: CHAR; METHODS show(); END
Many of these types are defined in interfaces. For example, the floating point types are defined in Real.i3, LongReal.i3, and Extended.i3, respectively. TEXTs are defined in Text.i3.
Comments are enclosed in the marks (* and *) as in Modula-2. Braces, { and }, are reserved for sets in Modula-3.
Modula-3 has retained the statement structure of Modula-2, which is similar to Pascal. Pascal programmers will need to note a few items however.
All compound statements are terminated. For example, the if/then statement has the form
IF a<b OR c < 0 THEN
SWAP(a,b);
END;
The form is the same whether you have one or many statements in the body of the IF. The "dangling else" problem of Pascal does not exist in Modula-3. The ENDs are always required. Note that operator precidence is such that parentheses are NOT needed in the test of this if/then statement. The precidences of the operators may be found in Appendix B. Also note that the Boolean operators, AND and OR, are "short-circuit" operators. Thus if a < b is true in the above, then c<0 will not be evaluated. This helps both efficiency and helps to avoid some errors. For example: b # 0 AND b DIV a > 5 will not fail when b = 0 as it might in Pascal. This is because when b # 0 (b is not equal to zero) is false, the AND is immediately declared false and so the second part, which would fail if evaluated, is NOT evaluated.
The IF statement also permits sequences of tests to be made with a simplifid syntax. For example, one could test an integer variable I for ranges with
IF I < 0 THEN
. . .
ELSIF I <= 5 THEN
. . .
ELSIF I < 10 THEN
. . .
ELSE
. . .
END;
The elipsis ( . . . ) in the above statement, and in many to follow, may be replaced with arbitrary sequences of statements. You can use as many ELSIF clauses as needed and the ELSE is optional, though you may have only one of these.
In the above situation we could also use a CASE statement if the I<0 and the I >= 10 cases require the same actions.
CASE I OF
| 1..5 => . . .
| 6..9 => . . .
ELSE . . . (* I < 0 or I >= 10 *)
END;
Again the ELSE is optional.
Modula-3 has the usual WHILE and REPEAT statements familiar to Pascal programmers, but it also has a LOOP statement, which implies an infinite loop. It may be exited with the EXIT statement.
LOOP
. . .
IF X < 0 THEN EXIT;
. . .
END;
The EXIT statement can also be used in the other iteration statements, though it is used so only infrequently.
The FOR statement is a bit unusual in that the loop control variable is not predeclared. It is defined within the statement itself and ceases to exist when the loop exits.
FOR I := 1 TO 10 BY 2 DO
. . .
END;
The body of the FOR will be executed for the odd values between 1 and 10. The BY clause is optional, in which case "BY 1" is assumed. The BY clause can evaluate to a negative value as well.
The WITH statement also defines a new variable with scope the WITH statement itself. For example if Employed is a pointer to a record with a field Name, then we might want a form like the following. It gives us access to the First and Last fields of the record Name.
WITH X = Employed^.Name DO
. . . X.First . . . X.Last . . .
END;
Note, importantly, that the variable X here is defined by the WITH statement itself. It should not be declared earlier.
Pointers are a bit more complex in Modula-3 than in its predecessors, though their use is very much easier. First, all pointer types are subtypes of a standard type, REFANY. (There is a small lie here. They might be subtypes of another type, ADDRESS, that we don't consider in this book. Such "UNTRACED" pointers do not have the advantage of garbage collection, which is also discussed in this section.)
A pointer or REF type is declared as in
TYPE
RefInt = REF INTEGER;
We could then create variables of this type with
VAR
p0, p1: RefInt;
The system will guarantee that these values are initialized to the value NIL, which has type NULL. If we want to create a new INTEGER in the TRACED HEAP, we do so with
p0 := NEW(RefInt);
Since Modula-3 uses structural type equivalence, we can create p1 with
p1 := NEW( REF INTEGER);
and p0 and p1 will have the same type. The name RefInt introduced in the type definition is a programmer convenience. The full type expression can be used in its place if desired. Here we have created two integers in the heap, but they don't have useful values. They do have values, however. Modula-3 guarantees that every variable always has a value legal for its type. We can assign new values to p0 with either
p0^ := 5;
p0 := 5;
The results are equivalent. Modula-3 does not require that we specify the dereference operator "^" unless it is needed to avoid ambiguity. For example,
p1^ := p0^;
implies that the variable pointed to by p1 is to get the value of p0, here a 5.
On the other hand
p1 := p0;
implies that p1 is to be an alias or additional reference to the same variable that p0 references. Then p1 will also have the same value as p0, but the original variable pointed to by p1 is no longer accessible. In this case the Modula-3 garbage collector will eventually discover that the old variable that p1 pointed to can be reclaimed and the storage reused. For values in the traced heap, there is no equivalent to the DISPOSE procedure of Pascal. Disposal is automatic. After the last assignment if we give either p0^ or p1^ a new value the other will be changed as well, since both p0 and p1 are references to the same variable.
The fact that RefInt is a subtype of REFANY is signified by the syntax
RefInt <: REFANY; (* Read: RefInt is a subtype of REFANY *)
The meaning of this is that a value of type RefInt can be assigned to a variable of type REFANY. More generally, a value of any subtype can be assigned to a variable of any of its supertypes. So if PTop is declared
VAR
PTop : REFANY;
then the following assignment is legal.
PTop := p0;
The opposite assignment is not legal, however, and if we tried to say
Wr.PutText(Stdio.stdout, Fmt.Int(PTop^));
we would get an error that PTop^ is not known to be an INTEGER; If we are certain that PTop points to an integer at run-time then we can force the compiler to accept this by applying the NARROW function as in the following.
Wr.PutText(Stdio.stdout, Fmt.Int(NARROW (PTop, RefInt)^));
The compiler will accept this, but will build in a run-time check so that if PTop does not hold a RefInt value at execution time the program will generate an exception, which can halt the program, or can be handled by the programmer. Information on exceptions comes later in this chapter.
A reference to an array can be used to set the length of the array at runtime. To do this we use an open array:
VAR A: REF ARRAY OF INTEGER;
in which we do not specify the index type. The index type will be assumed by the compiler to be [0..someMax], where someMax is not specified. In any case the index type is a subrange of CARDINAL. The variable, A, has value NIL initially as A is really just a pointer. When we have decided on the size of the array we can create it with
A := NEW (ARRAY OF INTEGER, size);
where size can be any CARDINAL valued expression. Then the value we have called someMax above will be size-1. We can then use A as an ordinary array whose low subscript is zero and whose high subscript is size - 1. For example
A[3] := 5; (* Equivalent to A^[3] := 5 *)
puts 5 in the fourth cell, provided 3 < size. As an aid to determining the legal subscript bounds of arrays you can use FIRST(A^) and LAST(A^) to get the actual low and high indices of the array (here 0 and size). The dereference operator is required here, however. Thus we can zero out the array with
FOR i := FIRST(A^) TO LAST(A^)
A[i] := 0;
END;
In object-oriented programming, which we shall study in this book, it is occasionally necessary to determine the type of a value at run-time. This was hinted at in the previous section where we indicated that a variable of a given type may hold a value of any of its subtypes. If we know what the type of the actual value is, we can use NARROW to recover the original type information. But what if we don't know, except that we know that the value has one of a few types? Modula-3 provides two additional facilities to help us here. The first is a TYPECASE statement, similar to the case statement, except that the cases are types rather than values. Suppose we have a variable X of type REFANY, and we know it is a reference to either an integer or a character. Suppose we wish to write X. If T is a variable of type TEXT then the following will do the job.
TYPECASE X OF
| NULL => T := ""; (* The empty string in case X = NIL *)
| REF INTEGER (Y) => T := Fmt.Int(Y^);
| REF CHAR (Y) => T := Fmt.Char(Y^);
ELSE T := "";
END;
Wr.PutText(Stdio.stdout, T);
When variable X has type REF INTEGER, the value of X will be assigned to Y and the following statement executed. Y is itself declared by its use in this statement.
The other feature is a type inquiry function ISTYPE. The first parameter is a value of any type and the second is a type. The result is a Boolean value, true if the value has the given type and false otherwise. Be careful because if the specific type of the first parameter is a subtype of the second (type) parameter, then the result will be true. We often use ISTYPE with NARROW. Suppose X has type REFANY. In the following, the variable I is defined by the with statement itself and should not be predeclared.
IF ISTYPE(X, RefInt) THEN
WITH I = NARROW(X, RefInt) DO
I^ := I^ + 99;
END;
END;
The value 99 will be added to the integer that X, and hence I, refers to. This code cannot fail at runtime since we only apply an integer operation to the value if we have checked that it is actually an integer.
Modula-3 is much safer than most other languages in regards to types and type errors. As many checks as possible are made at compile time. This increases type safety and gives a maximum amount of early information to programmers as they develop programs. Type safety does not come at the expense of flexibility, however, as run-time checks will be used where necessary. This permits the programmer to write programs that he or she can verify as correct, even though the compiler itself would consider them questionable. In the most recent example it is impossible for the compiler to verify that X^ := X^ + 99 is correct, though the programmer may know it to be (if X refers to an integer). If the programmer is certain then the typecheck (ISTYPE) is not needed. If the programmer is "certain" but wrong, the error will be caught at run-time, and the language provides other facilities for recovering from the error. If the programmer is not certain, then he or she can employ a type check or a typecase statement to explicitly cover the options.
Note, for completeness, that Modula-3 has some additional, lower-level, run time typing facilities in addition to the ones we shall use.
Procedures in Modula-3 are similar to those in Pascal. The main difference in syntax is that functions also use the introductory keyword PROCEDURE. They are distinguished only by having a return type given. A value is returned from a function with the return statement. In a function, the return statement has an expression argument. Note the equal sign that separates the "header" or "prototype" from the body and that the name of the procedure or function is repeated at the END.
PROCEDURE Min (x,y:INTEGER):INTEGER =
BEGIN
IF x <= y THEN RETURN x ELSE RETURN y; END;
END Min;
Procedures and functions in Modula-3 also have type. The type of the above function is
PROCEDURE (x,y:INTEGER):INTEGER;
Note that everything is there except the name of the procedure or function.
We could give this type a name, say CompareFunc with
TYPE CompareFunc = PROCEDURE (x,y:INTEGER):INTEGER;
We could then have a variable of this type and could assign the Min function above to this variable, and then call the function using the variable:
VAR compare: CompareFunc;
. . .
compare := Min;
y := compare(z,3); (* Min will be called *)
Procedures and functions can also have default arguments. This means that the actual arguments don't have to be given during the call. They will take the values assigned earlier as defaults. We could have defined Min as
PROCEDURE Min (x: INTEGER; y:INTEGER := 0):INTEGER =
BEGIN
IF x < y THEN RETURN x ELSE RETURN y; END;
END Min;
With this definition we need only supply a value for x and if only one parameter is supplied, then it will be compared to zero.
When you define or call a procedure or function with no parameters you DO need to write the parentheses even though there will be nothing between them. This makes it easier to distinguish a function call from the use of a variable when you read programs. Finally, note that it is possible to use the names of the parameters, rather than their positions, when calling procedures. For example, we could call the (most recent) Min function with any of the following forms.
. . . Min (3,4) . . . (*Usual positional arguments *)
. . . Min (3) . . . (* y defaults to zero *)
. . . Min (x := 3,y := 4) . . . (* Named arguments *)
. . . Min (y := 4, x := 3) . . . (* in any order. *)
One of the main uses of procedure types is to pass one procedure to another as a parameter. For example if we wanted to write a general Sort procedure, it would be nice to be able to let the user decide on the comparison that would be used, rather than commiting to one when we write Sort. To do this we pass a CompareFunc to Sort as a parameter. The protocol of Sort would be:
PROCEDURE Sort(A: someArrayType; Compare: CompareFunc) =
BEGIN
. . .
IF A[x] = Compare(A[x], A[y]) THEN . . . END;
. . .
END Sort;
The user would call Sort with a call such as:
Sort(A, Min);
Within Sort, a usage of the parameter Compare would then be a call to function Min.
Occasionally we write a function that does something in addition to returning a value. We then sometimes want to execute the function just for this effect and we don't need the returned value. In Pascal you need to declare a variable to accept the value when the function is called and then ignore the value of the variable. Modula-3 provides the EVAL statement for this situation. It takes any expression, not just a function call, and evaluates the expression, but does nothing with the returned value. There would be no point in it with the above example, but we could call Min with
EVAL Min(4,5);
If Min did something like write on an output stream then we would see that effect, but the value returned (4) would be ignored.
We shall make extensive use of most of these facilities in this book.
Large Modula-3 programs are broken up into a collection of small files. Some of these files contain public declarations, usually of types, procedures, and variables. These declaration files are called interfaces and are distinguished by having file names that end in ".i3" (dot i3). These files are meant to be IMPORTed into other files so that we may obtaining access to the declarations. Any procedures that have their declarations (name and parameters) in an interface must be defined. Commonly this is done in an implementation file, that may have the same name as the interface file except that it ends in ".m3" rather than ".i3". An interface, defined in an interface file, may IMPORT several other interfaces. Implementations EXPORT interfaces. This means that they implement the procedures, functions, and classes (defined later) that are declared by the interface exported. Usually an interface named mumble.i3 will be exported by an implementation contained in the file mumble.m3, but it doesn't necessarily need to be that way. In actuality an interface can be exported by several implementations, each of which implement only a portion of the interface. The relationships between the names of the interfaces and the names of the files in which they reside is also not specified by the language. This is the purpose of m3build. Usually, however, the file mumble.i3 will contain an interface mumble and the file Mumble.m3 will contain the module Mumble. Let's look a a very simple example.
In file Nothing.i3 we include the following three lines:
INTERFACE Nothing;
PROCEDURE Message(i:INTEGER);
END Nothing.
This file simply declares a procedure with an integer argument (and no return value) named "Message." The corresponding implementation file "Nothing.m3" for this interface would look like:
MODULE Nothing
EXPORTS Nothing; (* This line is optional, since they have the same name. *)
IMPORT Wr, Stdio, Fmt;
PROCEDURE Message(i.INTEGER) =
Wr.PutText(Stdio.stdout, "Hello World number: ");
Wr.PutText(Stdio.stdout, Fmt.Int(i));
Wr.PutText(Stdio.stdout, " .\n");
END Message;
END Nothing.
Here we define the function that was declared in the interface.
Another file that wanted access to this function would import Nothing to get access to the protocol for calling it, and a running program would be constructed by the linker by linking to the file Nothing.i3. We will see the m3makefile for this momentarily.
Recall that a program must export interface Main to be complete. Suppose that we have a module Main, in a file Main.m3, that contains the following.
MODULE Main; (* EXPORTS Main, of course *)
IMPORT Nothing;
BEGIN
Nothing.Message(365);
END Main.
Here the Message procedure from interface Nothing is called. Note the "qualified" reference, Nothing.Message, to an item declared in an imported interface. This permits us to name things freely, as long as we are careful to keep the names of the interfaces themselves distinct. This module main could also declare something named Message and there would be no conflict with the Message from Nothing which is known here as Nothing.Message.
The m3makefile would need to contain lines for Main, for Nothing, and for the library.
module (Nothing)
implementation (Main)
import (libm3)
program (test)
By saying "module (Nothing)" here we indicate that there is a pair consisting of an interface and a module with the same name, "Nothing." If we m3build this m3makefile, then we will have executable named "test" to run.
In procedural programming, complex data structures are usually built from pointers and records. In object-oriented programming we use classes instead. Pascal has a very complex record mechanism called variant records that allow things like lists and trees to be built. C has structs and unions. In Modula-3 we use classes. We shall study them in detail starting in the next chapter, but we note only a few things here. Classes define types. The values of those types are called objects. A class might be used to define the nodes of a linked list, or the list as a whole. The objects of the class would be individual linked list nodes or individual lists. Because of this, Modula-3 has a simpler record structure than Pascal or Modula-2. It is lacking variants. The power needed to build heterogeneous structures is conferred by classes instead. Before we take this up, however, let's look at an example that uses records and modules. The usual purpose of an interface is to export a type and procedures to manipulate that type.
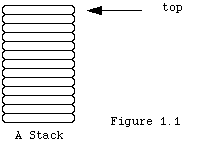
The idea of a stack is that it is a certain variety of storage mechanism for data of some kind. As it is a storage structure we must be able to insert data into it and later retrieve the data inserted. The insertion into storage is called push, and the removal is called pop. No other operation modifies the storage. Objects are removed (popped) in the reverse order from the order of insertion. This is called LIFO, for "last in- first out". One gets access to items stored only through reference to the top of the stack, the top being the most recently inserted item still remaining on the stack. A reference to the top of the stack is just called top. See Figure 1.1

Stacks arise frequently in computer science and in applications. For example if we were building a robot capable of walking a maze, it might be useful to organize its memory around a stack. In this way it could keep track of where it had been in the maze by pushing its coordinates onto the stack each time it moved. Then it could reverse its course when it encountered a dead end by popping a coordinate off its stack and returning to there. It would always have a path back to its starting point stored in its "memory."
In Modula-3 we may implement a stack (imperfectly) as follows. (Note that we are not yet taking full advantage of Modula-3. This is almost the same as what can be done in simpler languages such as Pascal. Following are two files defining a simple stack and a Main module to use it. Here we use the Modula-3 convention that the main type exported by an interface is named T. Since we use qualified references, it will be referred to as SimpleStack.T whenever we name it from outside the defining interface and module. Therefore, the names of modules themselves are usually what would be type names in other languages.
(* SimpleStack.i3 *)
INTERFACE SimpleStack;
TYPE
T = RECORD
elements: ARRAY[0..99] OF REAL;
top: INTEGER;
END;
(* Call INITIALIZE before using any SimpleStack.T *)
PROCEDURE INITIALIZE (VAR S: T) ;
(* Postcondition: S is empty);
PROCEDURE PUSH (VAR S: T; E: REAL) ;
(* Precondition: S not full *)
(* Postcondition: E = S.top *)
PROCEDURE POP (VAR S: T; VAR E: REAL) ;
(* Precondition: S not empty *)
(* Postcondition: -- see the next chapter. *)
PROCEDURE EMPTY(S: T) ;
PROCEDURE TOP(S: T; VAR E: REAL) ;
(* Precondition: S not empty *)
(* Postcondition: E is the top and S is not modified. *)
END SimpleStack;
(* SimpleStack.m3 *)
MODULE SimpleStack;
PROCEDURE INITIALIZE (VAR S: T) =
BEGIN
S.top := -1;
END INITIALIZE;
PROCEDURE PUSH (VAR S: T; E: REAL) =
BEGIN
IF S.top < 99 THEN
INC(S.top);
S.elements[S.top] := E;
END;
END PUSH;
PROCEDURE POP (VAR S: T; VAR E: REAL) =
BEGIN
IF S.top >= 0 THEN
E := S.elements[S.top];
DEC(S.top);
END;
END POP;
PROCEDURE EMPTY(S: T) =
BEGIN
RETURN S.top < 0;
END EMPTY;
PROCEDURE TOP(S: T; VAR E: REAL) =
BEGIN
IF S.top >= 0 THEN E := S.elements[S.top]; END;
END TOP;
END SimpleStack.
(* Main.m3 *)
MODULE Main;
IMPORT SimpleStack, Stdio, Fmt, Wr.
VAR S: SimpleStack.T;
SimpleStack.INITIALIZE(S);
SimpleStack.PUSH(S, 5.0);
SimpleStack.PUSH(S, 3.0);
SimpleStack.PUSH(S, 3.0);
SimpleStack.POP(S);
Wr.PutText(Stdio.stdout, Fmt.Real(SimpleStack.TOP(S)));
SimpleStack.PUSH(S, 2.0);
. . .
END Main.
We create an actual stack by declaring a variable to be of type SimpleStack.T and then calling INITIALIZE with this variable as parameter.
A visual picture of this implementation, after several pushes and perhaps some pops have been done is shown in Figure 1.2.
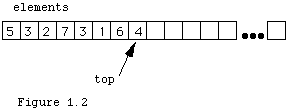
Note that the field top of the stack is actually an integer, here with value 7. The contents of cell 7 is 4 (actually 4.0: the data is REAL). We indicate this with an arrow to the cell with index 7. In fact it is fairly common in practice to say "pointer" for the value of an integer index into an array, and to say that top "points" into the array. This should not be confused with a Modula-3 pointer valued variable, though such a variable is actually very similar to an integer array index.
The precondition means that the user is responsible for something before calling a function or procedure. For correct use of one of these simple stacks the user must guarantee that the stack is not empty before calling POP. Likewise, we must guarantee that there are fewer than 100 elements in it before calling PUSH. Preconditions are an important means of communication between the designer of an interface and its user because they inform the user as to her or his responsibilities at the point of call of a function. They also inform the implementor of the interface under what conditions the functionality must be guaranteed to be error free. In other words, a precondition is a contract between a builder and a user stating responsibilities of each party.
Similarly, a postcondition, is what the implementor must guarantee to happen in all cases in which the function is called with a true precondition. This is the other half of the contract.
The user should have noticed that there is nothing special about a stack that stacks reals. We could just as well stack integers or other stacks for that matter. There are a number of ways to accomplish this without writing a separate stack module and interface for each kind of data that we might need. One way is to define a generic interface and module pair. We would normally do this in place of the simple stack above. In Modula-3 we might use the following generic interface.
GENERIC INTERFACE Stack(ELEMENT);
TYPE
T = RECORD
elements: ARRAY[0..99] OF ELEMENT.T;
top: INTEGER;
END;
PROCEDURE INITIALIZE (VAR S: T) ;
(* Postcondition: S is empty);
PROCEDURE PUSH (VAR S: T; E: ELEMENT.T) ;
(* Precondition: S not full *)
(* Postcondition: E = S.top *)
PROCEDURE POP (VAR S: T; VAR E: ELEMENT.T) ;
(* Precondition: S not empty *)
(* Postcondition: -- see the next chapter. *)
PROCEDURE EMPTY(S: T) ;
PROCEDURE TOP(S: T; VAR E: ELEMENT.T) ;
(* Precondition: S not empty *)
(* Postcondition: E is the top and S is not modified. *)
END SimpleStack;
GENERIC MODULE SimpleStack (ELEMENT);
PROCEDURE INITIALIZE (VAR S: T) =
BEGIN
S.top := -1;
END INITIALIZE;
PROCEDURE PUSH (VAR S: T; E: ELEMENT.T) =
BEGIN
IF S.top < 99 THEN
INC(S.top);
S.elements[S.top] := E;
END;
END PUSH;
PROCEDURE POP (VAR S: T; VAR E: ELEMENT.T) =
BEGIN
IF S.top >= 0 THEN
E := S.elements[S.top];
DEC(S.top);
END;
END POP;
PROCEDURE EMPTY(S: T) =
BEGIN
RETURN S.top < 0;
END EMPTY;
PROCEDURE TOP(S: T; VAR E: ELEMENT.T) =
BEGIN
IF S.top >= 0 THEN E := S.elements[S.top]; END;
END TOP;
END SimpleStack.
Now we can create a stack of reals by creating the following two very short files. RealStack.i3 will contain only
INTERFACE RealStack = Stack(Real) End RealStack.
File RealStack.m3 contains only one line also
MODULE RealStack EXPORTS RealStack = Stack(Real) End RealStack.
These are called instantiations of the generics. Recall that the system contains an interface Real.i3. A Main follows.
MODULE Main;
IMPORT RealStack, Stdio, Fmt, Wr.
VAR S: RealStack.T;
RealStack.INITIALIZE(S);
RealStack.PUSH(S, 5.0);
RealStack.PUSH(S, 3.0);
RealStack.PUSH(S, 3.0);
RealStack.POP(S);
Wr.PutText(Stdio.stdout, Fmt.Real(RealStack.TOP(S)));
RealStack.PUSH(S, 2.0);
. . .
END Main.
We can also use integer stacks by instantiating IntegerStack.i3 and IntegerStack.m3. However, here we don't have a built-in interface Integer.i3 to help us, so we need to provide it. This is so simple that we don't need an implementation.
INTERFACE Integer;
TYPE
T = INTEGER;
END Integer;
generic_module (Stack)
module (RealStack)
implementation (Main)
import (libm3)
program (test)
We will make some use of generics later in the book.
Exceptions indicate that an error or other "exeptional" condition has occurred in the running program. In Pascal, if you mistakenly divide by zero, the program just halts, hopefully with a message that helps you find the error. In more modern languages, such as Modula-3, what happens in such a situation is under control of the programmer, though if the programmer chooses not to exercise control then the system will enact some predefined behavior, such as halting the program.
Even if you don't use exceptions in your programs, you need to be slightly aware of them since the Rd and Wr interfaces use them extensively. You will get warnings about unhandled exceptions when you use these interfaces.
The user can define new exceptions. In the library that accompanies this book there is only one exception defined: fatal:
EXCEPTION fatal;
Exceptions are "raised" and "handled." Raising an exception means that the exceptional condition has occurred. The system will raise exceptions for dividing by zero, for example. We raise ratal when the user calls a procedure Object.Error, which takes a string as its argument. This procedure writes out the string and raises fatal with the statement:
RAISE fatal;
The procedure heading of this procedure indicates that the exception might be raised when the procedure is called. In this case fatal is always raised when we call Error, but that isn't so for all procedures that might raise an exception.
PROCEDURE Error(s:TEXT) RAISES {fatal};
We may include a whole set of exceptions with any procedure. If we ignore exceptions, then our programs will halt when they are raised. Often this is satisfactory, if your program is simple and only for yourself. In a large program to be sold to customers, that is seldom adequate. The buyers of software don't like programs to halt. They sometimes get very angry. They often buy products in the future from other sources.
We handle exceptions by surrounding statements and expressions in which they might be raised with TRY statement. For example, if we wanted to handle the fatal exception raised when we call error we would use something like the following:
. . .
TRY
. . .
Error("We seem to be out of barrakas.");
EXCEPT
| fatal => (* try to get more barrakas *)
. . .
ELSE
END;
Here we provide a "handler" for the fatal exception. By including an ELSE clause, wwe also provide a default, do nothing, handler for any other exception that might be raised in the try statement.
If an exception is not handled in a try statement it is "propagated" to an enclosing try statement. If there is none, then it will be propagated back through procedure calls looking for a try statement that handles the exception. If none is found, the system will handle the exception, probably by halting our program. If we propagate an exception to a procedure that doesn't list it in the raises clause then the system ignores the original exception and propagates the unhandled exception exception instead.
Abstraction is the means by which we control information overload. In programming it is achieved by designing packages of functionality that present a consistent, logical interface to "clients" that need the functionality. This helps programmers, and those who must understand the work of programmers, to deal effectively with the myriad detail present in any software system.
Object oriented programming helps with this in two ways. First it provides mechanisms by which the visibility of information may be controlled. This makes it possible to hide details of an implementation that are not needed by those who incorporate the functionality into other parts of the system. The second way in which object oriented programming aids in incorporating abstraction into programming is by presenting a simple model of computation that is similar to the world in which we live, and that makes it easy to design data elements of a system that present a simple interface to other parts of the system.
1. (1.5.2) Implement the Hello World program of Section 1.5.1.
2. (1.5.5) Write a program in Modula-3 to
(a) Read in 10 integers from Stdio.Stdin, echoing them to Stdio.stdout.
(b) Write out their sum and average.
Use a for loop to control the program.
3. (1.5.5) Repeat Exercise 2, using a while loop in place of the for loop.
4. (1.5.5 Declare an array
values : ARRAY[1..10] OF INTEGER;
5. (1.5.8) Repeat Exercise 4 with the following changes.
Use a procedure to read the values and another to write them. A third functional procedure will compute and return the sum of the array. Pass the array to them as an open array parameter (See Section 1.5.6). Retrieve the length within the procedures writearray and sumarray. Use the following prototypes;
PROCEDURE readarray(VAR A: ARRAY OF INTEGER; LENGTH: INTEGER);
PROCEDURE writearray(READONLY A: ARRAY OF INTEGER );
(* READONLY means that the procedure will not modify A *)
PROCEDURE sumarray(READONLY A: ARRAY OF INTEGER):INTEGER;
6. (1.5.8) Modify the following simple sort routine so that it takes a parameter of type CheckType and uses the parameter rather than the built-in operator < to compare the sizes of the two values.
TYPE CheckType = PROCEDURE(a,b:INTEGER):BOOLEAN;
PROCEDURE Sort(A: ARRAY OF INTEGER) =
VAR temp: INTEGER;
BEGIN
FOR i := FIRST(A) TO LAST(A) DO
FOR j := FIRST(A)+1 TO LAST(A) - i DO
IF A[j] < A[j-1] THEN
temp := A[j];
A[j] := A[j-1];
A[j-1] := temp;
END;
END;
END Sort;
Call this procedure with each of the two following CheckType procedures.
PROCEDURE less(a,b:INTEGER):BOOLEAN =
BEGIN
RETURN a < b;
END less;
PROCEDURE more(a,b:INTEGER):BOOLEAN =
BEGIN
RETURN a > b;
END more;
7. (1.5.9) Repeat Exercise 5, separating the three function prototypes into an interface with the implementations in a corresponding .m3 file. Write a Main module to call these and solve the problem of the exercise.
8. (1.5.9) To make certain that you can use your Modula-3 system, and that you understand multiple file linking and calling of procedures, create the following three files and compile and link them with m3build on your system. The purpose of the program is to write "Hello world." on the terminal screen.
File "test.i3" has only three lines.
INTERFACE Test;
PROCEDURE printIt(msg: TEXT);
END Test.
File "test.m3" has seven lines.
MODULE Test;
IMPORT Fmt, Stdio, Wr, Text;
PROCEDURE printIt(msg: TEXT) =
BEGIN
Wr.PutText(Stdio.stdout, Text.Cat(msg , Text.FromChar(`\n')));
END printit;
END Test.
The purpose of printIt is to output its parameter msg to standard output.
File "Main.m3" has seven lines.
MODULE Main;
IMPORT Test;
VAR hello : Text;
BEGIN
hello := "Hello world.";
Test.printIt( hello);
END Main.
9. (1.5.10) Build, run, and test the stack program presented in this chapter.
10. (1.5.12) Build and test the generic stack module of section 1.5.12. Also provide it with a new function so that a user could query a stack to determine if it is FULL.