How quickly Nature falls into revolt
When Gold becomes her Object!
Shakespeare, Henry IV, Part 2
Though this be madness, yet there is method in't.
Shakespeare, Hamlet II
What is it that we do when we program? How shall we best accomplish that task? What tools and techniques do we have available to aid us? What are the constraints that require us to behave in a certain way? What mental attitudes should we adopt to make it easiest?
These are important questions and the answers are not obvious. If they were easy to answer software would be cheap and simple to produce. As it is, it has taken us nearly fifty years of successive refinement of the problem to come to an approximation of the answers. In this section I will attempt to give answers to some of these questions, but it should be understood from the start that they are not the only possible answers. It is possible to give radically different answers to the questions and justify them completely.
It is advantageous to consider the programming process as a kind of modeling. Seen from a certain viewpoint a computer program is a concrete model of some system of phenomena. It is concrete since it may be manipulated directly (using a computer to execute it), it is a model since it was created in order to give answers to some problem that existed outside of the computer (or at least outside of the program itself). Payroll programs model a certain form of employee/employer relationship, spreadsheets model a certain way of thinking about formulas, word processing programs model a simple, linear, text creation method that existed before computers, and hypertext systems model a more sophisticated text creation/utilization method that has also been used for as long as books were printed on separate pages, had indexes, and could be "flipped" through. Even an operating system that controls the internal workings of a computer is a concrete expression of a simple management system (central control of scarce resources--distribution of workload among independent workers) that exists in similar form outside of computers.
Creativity in programming is, then, a form of creativity in modeling. What are the fundamental features of the "external system" that are to be included in the model? What are the features that are to be excluded? How are we to decompose the system to discover components of the model? How are we to compose the components of the model to construct the full model? How are we to verify that the model is "close enough" to the original system? More hard questions.
From a slightly different viewpoint, a computer program is a form of communication. One way to consider this is that a program is a way to communicate the needs of the programmer and her client to a computer. More importantly a computer program is a form of communication between people: the programmer and the client, the programmer and the manager, the programmer and the other programmers working on the same program, the programmer and himself. It is important to realize that computers don't need programs. All they need are instructions. The problem is that people find it hard to create the instructions without creating programs. Are you asking what is the difference between instructions and programs? Programs are composed of instructions certainly, but programs contain an organizational component that is not necessarily present in instructions.
In particular, computers don't need programming languages. Languages like Pascal, COBOL, C, Smalltalk and the rest exist because of the capabilities and limitations of people, not because of the capabilities and limitations of machines. The two most important limitations of people are that we have a limited attention span and a limited short term memory capacity, especially for detail. The most important capabilities of people are that we are adept at language and at abstraction. Our ability, in C, Pascal, and Modula-3, to define data types and procedures aids us in both overcoming our limits and playing to our abilities since we can lessen the detail load (a record may be used rather than all of its components) and build deep abstractions, aided by our language facilities.
Webster gives several definitions of "Abstract": disassociated from any specific instance; difficult to understand; ideal; expressing a quality apart from an object. The antonym of abstract is usually given as "concrete." The process of abstraction involves discovery of some essential aspect of an object or group of objects and giving that aspect a name. For example "goodness," "truth," and "beauty" are properties of human beings, and so
"Goodness," "truth," and "beauty" are abstractions. (Definitions in this section are derived from Webster's Dictionary)
The second definition of abstract, difficult to understand, derives from the fact that it is often difficult to give definitions of a particular abstraction that are not self referential. Dictionaries define "goodness" as "the quality or state of being good." Good is defined as "something that is good." Abstract entities are also defined in terms of other abstractions. Good is also defined as "something conforming to the moral order of the universe." But "moral" is another abstraction. In fact definitions generally require that the user go through the same process of discovering the essential aspect that the creator of the original abstraction did. A set of concrete examples is used that embody a concept or its opposite and the user is invited to go through the process of abstraction to discover again the idea at hand. This works because people are good at abstraction.
In the first chapter we discussed the "rule of seven" that indicates that our mental equipment is limited in its ability to retain certain kinds of detail in short term memory. We also indicated that the ability to form abstractions largely compensates for this in practice. This is just another way of saying that we have an ability to discover and to impose structure on the world. As an example of what is meant by this, perform the following two-part experiment.
Take as long as you want to memorize the following collection of numbers: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40. Now repeat the numbers you just memorized without looking. No problem. Now do the same with the following numbers: 30, 40, 22, 32, 36, 20, 34, 24, 4, 18, 26, 6, 2, 38, 16, 12, 28, 8, 14, 10. This latter problem is very much harder. Probably you gave it up after discovering my (abstract) point that structure helps. The first problem has a definite structure: even numbers between 2 and 40. The second problem has no such structure and so is harder to do. In the first problem it is the structure that is easily discovered and remembered. This structure is a low level abstraction.
We can use this abstraction to build higher level abstractions such as "the sum of the first twenty positive even numbers." This sum can be easily done in the mind if we remember that the sum of the first N positive numbers is N(N+1)/2, so the sum of the first N even numbers would be twice this (by the distributive law, which is an abstraction), or N(N+1), so that the sum of our numbers is 20 times 21 or twice 210 or 420. Now if we discovered that the second collection of numbers was just a permutation (an abstraction) of the first set of numbers and the fact (abstraction) that the sum of a set of numbers is the same as the sum of any permutation of those numbers (abstraction), we discover that the sum of the second collection of numbers is also 420 (concrete fact).
Structure and abstraction as a means of overcoming complexity has another benefit. Synergy is the idea that the whole of something is more than the sum of its parts. An automobile may be described as "a human controlled, fuel powered, ground based, transportation device." This is too broad to serve as a definition of automobiles as it is also a description of a bus and some other things. But if you look at the parts out of which an automobile is constructed, none of them alone implies this description. The wheels imply transportation, the engine implies fuel power, and the instrument panel implies human control, but each of these components is usable in other contexts and none by itself implies "automobile." It is the combination of these things that gives the essence of an automobile. This is synergy. It is also illustrated by the proverb of four blind Indian wise men encountering an elephant for the first time. One exploring the flank describes an elephant as being "very like a house," another feeling only the trunk describes it as "very like a snake," the third at the tail exclaims "very like a vine," and the last believes it to be "very like a tree," encountering only the leg. In fact an elephant is more than the sum of its parts.
In computer programming we would like to apply these ideas of abstraction, structure, and synergy to the creation of software systems. The need to do this arises from the fact that all non-trivial programs contain a complexity of detail that is beyond our capabilities to understand without resorting to structure. It is for this reason that assembly language is harder to write and to read than Pascal. It contains more detail and requires that the programmer keep track of more detail. It is also the reason that assembly language is called a "low level" language and Pascal a "high level" language. Pascal embodies a higher level of abstraction than assembly language.
There are several different kinds of abstraction that we use in programming. In the next sections we will discuss two main forms of abstraction: procedural abstraction and data abstraction. Object oriented programming embodies both of these and goes a step beyond them.
When we write a procedure in Modula-3 we create a set of instructions that does some particular task. Generally this task may be quite complex in detail but can be described succinctly in words. We give it a name that is a single word or short verb phrase describing what it does. We use verbs because procedures are actions. (Functions are similar but are described by noun phrases describing the function result.) For example, a procedure that computes the balance in an accounting system might be given the name ComputeBalance. The procedure would have as input parameters an account number or name and as output the balance of that account. The name of the procedure is an abstraction that stands for the complexity in the code itself.
Procedural Abstraction Naming a segment of code so that it may be manipulated (usually just executed) by giving its name. |
One important aspect of procedural abstraction is parameterization. We may separate what is fixed in a procedure from what is variable, and parameterize the variable part. Often it is the data that the procedure is to manipulate that constitutes the variable part, but it could, in general, be anything. With parameters the procedure becomes more useful because we can use it in several contexts.
Since procedures may be called from other procedures we have the basis for higher level abstractions built from low level abstractions. For example our ComputeBalance procedure would appear in a payroll program which is just a higher level abstraction than ComputeBalance.
Procedures in Pascal and Modula-3 may be nested, or defined inside of one another. When this is done the local variables declared in the inner procedure are not visible to the containing procedures or the main program, and are allocated on the system stack, so that they only have allocated storage when the procedure is actually executing. The purpose of this is to permit and encourage a top-down hierarchical program design style with either top-down or bottom-up programming. In C and C++ procedures may not have nested definitions, but they may be called in nested fashion and so have nested lifetimes of execution. In top-down hierarchical design one thinks of the entire programming project as a single procedure ("main"). The designer then uses whatever creative facilities are available to decompose the overall problem into smaller sub problems, with the following three properties: (1) each sub problem can be solved with a (perhaps very complex) procedure; (2) the sub procedures implied by (1) may be synthesized or composed into a whole; and (3) the resulting composition solves the original problem, or in other words is equivalent to the original hypothesized procedure. One then attacks the sub problems of (1) above in the same way so as to actually create the implied procedures.
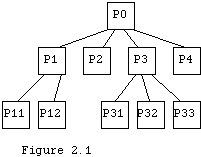
The resulting program is then written down with sub procedures from the sub problems being conceptually nested in the procedures of their parents. If a procedure/problem has sub procedures/sub problems then the statements of the associated statement part simply express the way in which the sub problems were shown to be composed in (2). For example if we decided in, attacking problem P1 of Figure 2.1, that we could solve it by executing P11 three times followed by executing P12 once then the procedure body for P1 would have a call to P11 in a loop to be executed three times followed by a call to P12. Problems that may be solved directly and simply without decomposition form the lowest level in our hierarchy.
Pascal has nested procedures because at the time it was created this method of program development, also called procedural decomposition, was seen to be a very important and efficient development style. The successors of Pascal such as Modula-2 and Modula-3 have kept this structure. The process is illustrated by Figure 2.2, in which we take the "solve" step of the figure to be a repeat of the overall process applied to the pieces whenever a piece is "complex," but simply programming if a piece is "simple."
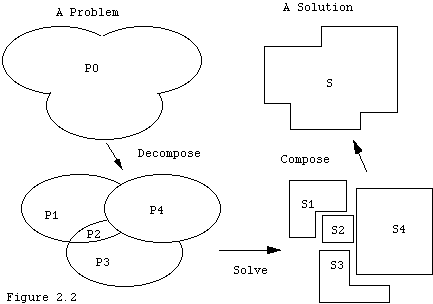
This technique is often called "divide and conquer" and is a general modeling technique. To model some phenomenon P0, look at it as a collection of sub phenomena P1, P2..., interacting in some way. Model each sub phenomenon, perhaps using further decompositions, and then "paste" the solutions or models of the sub phenomena together according to the interactions discovered during the original decomposition. Note that the beginning and ending figures were not drawn to be identical as the model always leaves out some detail deemed to be non essential. A model is thus a "faithful representation" of the original only for certain purposes.
We would like to note, importantly, that different languages support procedural abstraction with different degrees of completeness. Pascal's implementation of procedures is somewhat flawed because procedures may only be used in very limited ways. We may declare a procedure, we may call a procedure, and we may pass a procedure as an argument to another procedure. Procedures may not be modified by a running program, and variables may not have values that are procedures. Note that Scheme allows both of these to occur and Modula-3 permits the latter. The implication of this is that in a Pascal program, except for procedure valued parameters, at each point at which a procedure may be called, the compiler knows exactly which procedure will be called. Sometimes it is desirable to postpone the decision as to the particular procedure called until the program is actually running. This "late binding" of procedures does occur in the case of procedure valued parameters as shown by the Modula-3 example below.
Suppose that we have an array type in our program:
TYPE DataArray = ARRAY [0 .. size - 1] OF REAL;
TYPE Modifier = PROCEDURE (VAR R: REAL);
Then we may have several arrays of type DataArray and also several procedures of type Modifier. Suppose that at various points in the program we need to apply some procedure of type Modifier to each of the reals in one of these arrays and that at different points in the program we need to apply different procedures to one of these arrays. This process of applying some procedure to each element of some array may be abstracted out of our system by declaring a procedure as follows:
PROCEDURE Apply(VAR A: DataArray; Proc: Modifier) =
BEGIN
FOR i := 0 TO size - 1 DO
Proc(A[i]);
END;
END Apply;
Apply(AccountArray, Increment);
and the effect would be the same as if we had written:
FOR i := 0 TO size - 1 DO
Increment(AccountArray[i]);.
END;
However, the compiler that translates this program has no way to know which actual procedure will be substituted for the formal parameter Proc so that the encoding of the procedure Apply will be generalized to permit any procedure with a single REAL VAR parameter to be used. What actual procedure is used is only determined at run time, not at compile time.
The above example illustrates that there is flexibility and hence power to be achieved by delaying certain decisions until late in the Think-Write-Compile-Test-Run software development process. Delaying decisions such as what procedure to use permits later decisions to be made in a more general way, hence more flexibility.
The flip side of this coin however is that there is safety in making decisions early in the cycle. In fact if all decisions can be made before the compiler translates the program into machine code then a good compiler can do a maximum of providing warnings of potential and actual errors, and can do a maximum of optimization. If decisions are made early then the program is more specialized and hence has more information that may be taken advantage of. This is the chief reason for Modula-3's strong typing mechanism. It permits the compiler to issue warnings of type inconsistencies which usually signify programmer errors. Since the compiler issues the error messages we learn of them earlier than if they occured only at runtime.
As a final note on procedural abstraction and our divide and conquer methodology, note that one can divide-solve-compose using criteria other than procedural decomposition. It is not necessary to divide up a problem according to processes that will solve it. In fact object oriented programming uses a divide and conquer method but divides up the problem and creates a solution using a different decomposition: decompose into the objects or actors in a system rather than the actions. More on this later.
The idea of data abstraction exists independently of computer programming and is properly a topic of mathematics as well as computer science. The term wasn't used, however, until the need for it appeared in computer programming.
Data Abstraction A data abstraction consists of three parts: (1) a set, S, of objects, which has elements whose representation structure is undefined; (2) a set, P, of operations defined on elements of S; and (3) a set, R, of rules that define the behavior of the operations and relationships between elements of the set. |
For example, by this definition, the Natural Numbers S= {1,2,3, ...} of mathematics with operations P= {+,-} and the usual Peano axioms R = { 1 is a Natural Number, every Natural Number has a unique successor, ...} is a data abstraction. I have actually given more here than is necessary, as I have shown a particular representation of S, which is not required. An alternate form of S is:
S = {{},{{}},{{{}}}, ...}, where {} represents the empty set, {{}} is the set of one element containing the empty set, etc.
Note that the type INTEGER in Modula-3 is an attempt to model a data abstraction, namely the integers of mathematics, though it does so imperfectly. In particular, int models only a bounded section of integers. It is -2,147,483,648...+2,147,483,647 on many computers.
In practice the above definition of data abstraction is a bit too narrow. We will use it however to define a slightly richer idea called an Abstract Data Type, or ADT.
Abstract Data Type An ADT is a set of data abstractions, each with its own elements, operations and rules, where one of the data abstractions within the ADT is specified as the principal data abstraction. |
Thus an ADT is a collection of interrelated data abstractions. There are operations and rules for each individual data abstraction. There may also be rules for combining and relating elements of different data abstractions. In many cases an ADT consists of only a single data abstraction. We will later see many examples of the more complex case. At this point I will only give an analogy to illustrate the general idea.
Consider the situation of the real business world. There we have people and also corporations. People do things (operations) and also relate to one another (rules). The same is true of corporations. But we also have behaviors of people and corporations to each other, such as people buying stock in corporations (a higher level operation), and these behaviors must obey certain laws and expectations (rules). Thus an ADT for the business world would contain at least a data abstraction for people and another for corporations. One of these would be designated as primary, depending on the specific needs of the system.
One example of an ADT, closely related to computer programming, as we shall see later, is the idea of a "List," like a shopping list. A List is a finite sequence of items of a certain kind. We can add to the list and delete from it in different "places," even in the middle. For example we might insert "Cheese" into the list "Bread," "Milk," "Eggs" just after "Milk." There may or may not be a particular ordering of the items in a List. A related data abstraction is that of a "List Position." This abstraction has "values" like "the position of item `Milk' in the List `Bread,' `Milk,' `Eggs'". The two data abstractions "List" and "List Position" could be bound together to form an ADT.
Another simple and useful ADT, with only one data abstraction is that of a STACK. We assume that some readers are familiar with stacks and have programmed them in the past. We shall give several ways to define and implement stacks in this and following chapters by way of introducing ideas and syntax of Modula-3. The final definition won't be given until Chapter 7. Now we want to simply discuss a stack as a data abstraction and show some simple operations that it uses. We shall use a subset of Modula-3 that is almost like Pascal. Later in this chapter we shall examine one that uses more features of Modula-3. While our ultimate goal is to present such ADT's in an object-oriented fashion, these first few examples do not yet employ any object-oriented features.
In Section 1.5.11 we examined simple stacks. Let's look at them again. To show a stack as an ADT we must describe its only data abstraction by giving the three sets, S of objects, P of operations, and R of rules. The set S contains just one element, the stack itself, and its structure is undefined. In practice it could be an array, but it need not be and making it an array would restrict it to contain some fixed maximum number of elements. It is important in its specification to leave the internals of this object undefined. The set, P, of operations consists of at least the operations push and pop. In reality it will need at least one more operation initialize, which guarantees some specific state of the stack. Since a stack is a storage mechanism this initial state is usually the empty state, so that it represents an empty storage. It will also be useful to have an operation (actually a function) that tells us if the stack is empty or not. This function could be named empty. Such a function that returns a truth value (true or false) is called a predicate.
The rules, R, for a stack are as follows. Immediately after initialize we find that empty returns true. Immediately after push we find that empty returns false. Whenever empty is true we find that top is an error and that pop is an error. Immediately after push has inserted X we find that top is X, and that pop returns X. Finally if the stack is in some state Y then applying push followed by pop will leave the stack in state Y.
There are some additional operations that may be useful for stacks. One of the most common is a function numberOfElements, called cardinality by mathematicians, that tells us how many data items are currently stored in the structure. To add such an operation it is necessary to define it, and we do this by adding additional rules. In this case the rules needed are: empty is true if and only if numberOfElements is zero; if numberOfElements is N and we execute push then numberOfElements is N+1, but if we execute pop instead then numberOfElements is N-1.
It is important to remember that it is the operations and their rules that define what a stack is. It is not the representation of the set on which the operations act. Any representation can be a stack as long as it has the required operations and that the operations obey the rules.
Within certain limits the implementation shown in Chapter 1 obeys the rules for a stack, but it is useful to catalog the ways in which it does not obey our definition. The most obvious is that there is nothing in the definition of a stack that implies that a maximum of 100 items may be stored at one time, but this is clearly a property of our implementation. Thus we have actually implemented a different abstraction called a finite or bounded stack. Secondly our implementation only permits real values to be pushed. Thus we have a bounded stack of reals, and not a stack per se. Finally, where the specification calls for errors we have actually implemented no-ops, i.e., no operation is done and the call leaves the state unchanged. In order to generate errors we may remove the if tests in PUSH, POP, and TOP and let the run time system halt our program when it makes a reference to an element not in the array (assuming it will, which is not always a valid assumption). Alternatively we may provide a general error handler within our program. One way to do this is to provide a simple procedure named error, that when called will print some message and then halt the running program. We may then modify PUSH, POP, and TOP so that if the if clause is false we call error. This latter method is preferable.
Now we should verify that, with the exceptions noted above, our implementation meets the specification. First we note that, as a storage mechanism, this implementation stores those real values which are in cells 0 through top, inclusive. What values there may be in cell of index larger than top are not important.
Assume that the stack is named S. Initialize sets S.top = -1 and EMPTY is true iff and only if S.top < 0 so our first rule is true for this implementation.
No operation can make S.top < -1, since only POP decreases it and it won't do that unless it was previously >= 0. Likewise PUSH always increases S.top so that after a PUSH, S.top is always >= 0, so that EMPTY is false, so the second rule is met.
Our third rule is met in the sense that both POP and TOP do nothing when the stack is empty (S.top < 0) and we may interpret this as a simple form of error. Including the error handler would improve our adherence to this rule.
Immediately after PUSH is executed, provided that the stack was not already "full," we see that S.top contains a reference to the array element inserted by PUSH. In these cases then S.top will reference this last inserted element and POP will return it, so that our fourth rule is OK.
Immediately after PUSH, if the stack was not "full" then a POP will remove the element inserted, and return S.top to the value it had before. Therefore from a logical standpoint the stack is in the same state that it was in before we did the PUSH. Note that it may not be in the same actual physical state, since there is a value at the next cell beyond S.top that was probably not the same before the PUSH. But, as this item is not logically stored in the stack, this is immaterial.
Note that in verifying the last two rules we had to provide for exceptional cases. That is to say if we push onto a full stack and then POP we will not return to the original state. We could give operations and axioms (rules) for a bounded stack that would define pushing onto a stack that held the maximum number of elements to be an error. This implementation would then, perhaps, fully meet such a definition. The reader is encouraged to give this definition and to do the necessary verification.
An "logical interface" for this stack type is a list of type names and function headers annotated with information necessary to the user. One purpose of the interface is that the user of a stack should not have to depend on reading the specific code of the functions. After all, this code might need to change, either because errors are discovered, or because the designer and/or builder discover a more appropriate mechanism. An informal interface for the stack type might be something like the following. Note that it isn't quite legal Modula-3 code.
Stack.T;
(* A type representing a bounded LIFO storage structure. It is limited to containing
no more than 100 items simultaneously. *)
PROCEDURE INITIALIZE (VAR S: Stack.T) ;
(* This must be called once before the stack S is first utilized.
It may be called again to clear its storage. *)
PROCEDURE PUSH (VAR S: Stack.T; E: REAL) ;
(* Precondition: S has been INITIALIZED and contains less than 100
items. Postcondition: E will be saved at the "top" of S. *)
PROCEDURE POP (VAR S: Stack.T; VAR E: REAL) ;
(* Precondition: Precondition: S has been INITIALIZED and is not
empty. Postcondition: The "top" of S will be returned in E and removed from the
storage. *)
PROCEDURE EMPTY(S: Stack.T) ;
(* Precondition: S has been INITIALIZED. Postcondition: Returns TRUE if
and only if the stack S is currently empty. *)
PROCEDURE TOP(S: Stack.T; VAR E: REAL) ;
(* Precondition: S has been INITIALIZED. Postcondition: The top of
S will be returned in E and the storage left unaffected. *)
Deciding whether our imperfect implementation of stack is adequate or not depends on the use to which it is to be put. If we are writing a simple program to be executed a few times by its creator it is probably OK, even with its flaws. If it is to go into a large software system it may be OK or not depending on the specification of the overall system and its projected lifetime. If it is to be put into a library of software to be used in several projects by one or several programmers over a long period of time, it is certainly inadequate. In the last situation it would be necessary to define what we mean by "error" and to implement error handling faithfully and either to remove the boundedness limitation or to give rules that clearly indicate what happens when the bounds are reached.
It is instructive to compare this implementation with another, based on different Pascal-like constructs. In this case we shall use pointer variables. If you are not familiar with these then you should consult the appendices for a discussion of pointer types and the underlying machine model that we are using, especially the information on the system heap.
Again we need to define one or more types, so that we have an implementation of the data set of the abstract data type, and also define several operations on this type, and then verify that the rules are true.
INTERFACE LinkedStack;
TYPE
T = POINTER TO StackNode;
StackNode = RECORD
element: REAL;
next: T;
END;
PROCEDURE INITIALIZE (VAR S: T);
PROCEDURE PUSH (VAR S: T; E: REAL);
PROCEDURE POP (VAR S: T; VAR E: REAL);
PROCEDURE EMPTY(S: T);
PROCEDURE TOP(S: T; VAR E: REAL);
END LinkedStack.
MODULE LinkedStack;
PROCEDURE INITIALIZE (VAR S: T) =
BEGIN
S := NIL;
END INITIALIZE;
PROCEDURE PUSH (VAR S: T; E: REAL) =
VAR aNode: T;
BEGIN
aNode := NEW(T);
aNode.next := S;
S := aNode;
aNode.element := E;
END PUSH;
PROCEDURE POP (VAR S: T; VAR E: REAL) =
BEGIN
IF NOT EMPTY(S) THEN
E := S.element;
S := S.next;
END;
END POP;
PROCEDURE EMPTY(S: T) =
BEGIN
RETURN S = NIL;
END EMPTY;
PROCEDURE TOP(S: T; VAR E: REAL) =
BEGIN
IF NOT EMPTY(S) THEN E := S.element; END;
END TOP;
END LinkedStack.
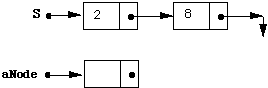
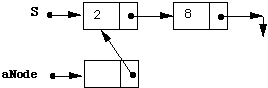
In the previous case we had an implicit property of the implementation, namely that the field variable top was always >= -1. In this implementation we have a different property maintained by the operations. Namely, our stack consists of zero or more nodes and either the stack variable itself, in the case of zero nodes, or the next field of the node that has existed for the longest time is equal to NIL. In Modula-3, NIL is not a node. It is a reserved word in the language. The run time system has some way to set its state so that it can test for equality to "NIL" but otherwise a pointer variable whose "value is NIL" does not behave like a node. In particular when P=NIL is true for some pointer variable P, then it is illegal to dereference P. Modula-3 programs have many tests to check for this case. Therefore S.element only appears inside an if statement that guarantees S <> NIL. A possible picture of our stack is shown in Figure 2.3, where pointer variables and fields are represented by arrows, and NIL is represented by a pair of arrows at right angles. Each box represents an instance of a stackNode record and each sub rectangle represents one field. In this case there have been four more pushes than pops, and the top is currently 5.
If you have had little experience with pointer variables the following pictorial trace of the stack operations may be helpful. We intersperse the program with pictures showing after each statement the effect of the statement on the state of the memory. We don't trace TOP or EMPTY as they don't change the state of the stack itself.
PROCEDURE INITIALIZE (VAR S: T) =
BEGIN
S := NIL;
END INITIALIZE;
PROCEDURE PUSH (VAR S: T; E: REAL) =
VAR aNode: T;
BEGIN
aNode := NEW(T);
aNode.next := S;
S := aNode;
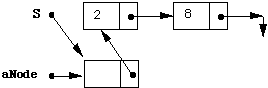aNode.element := E;
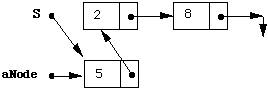END PUSH;
PROCEDURE POP (VAR S: T; VAR E: REAL) =
BEGIN
IF NOT EMPTY(S) THEN
E := S.element;
S := S.next;
END;
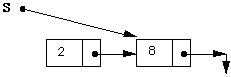END POP;
At this point there is no pointer to the node that contains the 2. The garbage collector will eventually discover this and will recover the storage that it occupies.
We must again verify that the axioms for a stack are true, or discover in which ways they are not. As mentioned above, the boundedness property of the last implementation has been relaxed, though not entirely overcome.
INITIALIZE sets the stack variable to be NULL and EMPTY tests for NULL so that our first rule holds.
PUSH always sets the stack variable to the result of a call to new which is never NULL unless the system is out of memory so that except in this case the stack is never empty after a PUSH and so the second rule holds partially.
If EMPTY is true then the stack variable is NULL and both TOP and POP are no-ops (rather than errors), which is the same as before for the third rule.
If we have just pushed a real value X then the stack variable is set to point to a node that contains X. POP and TOP return the value in such a node, so then fourth rule holds.
The last rule holds as well since PUSH copies the old stack variable value into the next field of the new node in the push operation. A POP operation sets the stack variable to be the next field of the node pointed to originally by the stack variable.
Again, our implementation would be improved by the implementation of an error handler, and by the presence of more checking, especially in the push operation to see that the call to new succeeds. Properly speaking we should either make such modifications or change the specification (the rules) to more clearly describe what we have done. For example in this case we could add a rule that an implementation on a finite machine could behave unpredictably if there was insufficient space in the memory to hold all the storage implied by the operations on the stack. This rule might be called the "cop out" rule, but it is at least a warning to users that our implementation may have holes.
When Pascal was created in the late 1960's it was a breakthrough language in that it made it possible for the user to create named types and to use them to control access to the low level representation (bits) of the data manipulated by a program. It also became possible to give types for the parameters of a procedure that permitted a form of contractual agreement between a procedure that performs a service (a server) and the procedure that needed the service (a client). Thus, programmers were freed from the necessity of continually remembering all of the details of the encodings that they used to represent program data.
In the FORTRAN world, if you wanted to pass a procedure the information that an employee was male or female, you passed an integer parameter with the value 0 or 1 (or similar). You would need to name the parameter carefully so that a user of the procedure would not try to pass the value 55. It was not possible to get the compiler to check for valid values. Therefore, either the programmer had to verify all such low level data by hand, or had to encode tests into the program to check for validity of the data. Both of these methods require a cost in time, and the latter has an additional cost in the length and complexity of the code. Types permit the computer itself to carry out this task in an efficient way. Additionally, strongly typed systems, and compile time typed systems in particular, provide a maximum of information to the program author as early as possible in the development process, i.e., at compile time.
Object oriented programming is another step in the same direction, automating low level detail, giving the computer and the compiler additional tasks that programmers otherwise need to perform, and making the text of the program more nearly like the high level description of the problem that it is designed to solve. In object oriented systems there is an extra level of binding between procedures and the data that they manipulate. In Modula-3, as in Smalltalk and C++, an object is actually a collection of data that "knows" what procedures may be applied to it. It is thus easier for a program author to guarantee that only appropriate operations are applied to a bit of data, because she or he designed the appropriate operations when the data was defined, and the object oriented system sees to it that other operations are not applied to the data object.
Object oriented programming, however, has another benefit, since it makes it possible, and easy, to make the running program more nearly model the real world situation in which the original problem arose. It is only a small leap to imagine that every program is a simulation or a model of some other phenomenon.
Object oriented programming consists of two tasks. The first is to partition the text of a large program into definitions of a certain kind, called classes. The second task is to partition the running program into data elements of a certain kind called objects. The relationship between the classes and the objects is that the classes are static descriptions of the dynamic objects. The programmer actually writes the text of the program, which is the static description, but must design both the static and dynamic aspects of the system.
Object Oriented Programming (first version -- of three) Programming methodology in which the data elements (objects) in the system form the fundamental unit of program decomposition. |
A class is a description of a collection of objects (or occasionally a single object). A class description tells about the data elements of the object that it uses to maintain its "state." These data elements are called its fields, or instance variables. The class description also tells about what operations may be applied to the objects of the class and ultimately how the data elements are changed to reflect the changed state of an object. These operations are called methods, and in Modula-3 we have both functional and procedural methods. We will use classes to model individual data abstractions and we will use Modula-3 interfaces to model ADT's.
The following is the class definition of a randomized five point star, which is a type of graphic object that might be important in a graphics application:
TYPE
S5PointStar = OBJECT
fDiameter: REAL;
fLocation: Point;
fImbalance: INTEGER;
METHODS
init5PointStar(imbalance: INTEGER; Loc: Point; Diam: REAL): S5PointStar;
draw(fill: Pattern);
moveTo(newLocation: Point);
END;
If we should create such a new five point star and then draw it we might see something like Figure 2.4.
Objects are referenced by variables whose names we declare in the declaration section of the program.
VAR myNewStar: S5PointStar;
A variable whose type is a class type will be called an "indirect variable" or a reference variable. Objects referred to by indirect variables are sometimes called indirect objects. Some languages, such as C++ have a kind of object that is not referred to indirectly, but behaves much more like a record with attached procedures. These would be direct objects.
Indirect Variable A variable whose type is a pointer type or a class type. Indirect variables are used to "refer" to objects in object oriented programming. |
To create and use indirect objects we declare a variable to have a class type. The declaration itself does not create the object. Instead we must call the standard function NEW to create the object. The object is then created in the area of system memory known as the "heap." The object lives until the garbage collector determines that the object can no longer be used in the program because no variable refers to it. Therefore, to create an indirect 5 point star we would first declare :
VAR myNewStar: S5PointStar;
We would then have to actually create the object with NEW. We will, of course, have to initialize the resulting object also, since its creation leaves it uninitialized. Here we could say:
myNewStar:= NEW(S5PointStar).init5PointStar( 5, aPoint, 7.2);
The NEW function takes a type as its argument and returns a reference or pointer to a value of that type. In this case we get back an uninitialized S5PointStar. We can then apply the initialization method directly to this object using the above syntax. Note that the initializer init5PointStar is also a function returning an object (it returns the same object actually, after initializing it). It is this final result that is assigned to the variable myNewStar.
An object created in this way will not need to be explicitly deleted by the programmer when there is no longer a need of its services. This is done automatically by the garbage collector. This service of the Modula-3 system helps to prevent many programmer errors, since it is sometimes extremely difficult to determine when an object is no longer accessible.
Creation of an indirect data object requires that we allocate the object, and then initialize it. However it is possible that the allocation could fail. Computers have only a fixed amount of memory. The following takes care of this:
myNewStar := NEW( S5PointStar)
Object.FailNil(myNewStar); // halt the program if myNewStar is NIL
EVAL init5POintStar(40,ctrPt,80.0);
The EVAL statement simply ignores the result of the expression that it is applied to; in this case the function call of init5PointStar. We assume of course that the variable ctrPt was already defined appropriately. The first statement is a call to the Modula-3 allocation operator. Thus, objects exist in the physical machine in the heap area of the memory. NEW allocates heap space for the object. The parameter indicates the type of the object (or reference value) to be returned.
The call to FailNil is a safeguard that is needed since NEW is occasionally unable to allocate the required space for the new object. The statement will cause the running program to halt if NEW was unable to find the required memory. This procedure FailNil is exported by the interface Object.i3, as shall be seen in Chapter 3.
Because the three-statement fragment of initialization code shown above is a very common pattern, we shall generally provide a function that contains it when we define any new class. For S5PointStar class our function it will be called New and it is shown below:
PROCEDURE New(imbalance: INTEGER; Loc: Point; Diam: REAL):S5PointStar =
VAR result: S5PointStar;
BEGIN
result := NEW(S5PointStar);
Object.FailNil(result);
EVAL result.init5PointStar(imbalance, Loc, Diam)
RETURN result;
END New;
This generator will return properly initialized stars to us. A drawing application could call this function several times to populate the sky with random stars. Each call will result in creation of a new object. Memory is allocated for our indirect objects from an area of computer memory called the HEAP. Unlike the local data of procedures this memory is not automatically deallocated when a procedure returns, so it is used to create relatively long lived items. A reference to the created object is returned by this function and the caller will generally assign the result to some variable or otherwise guarantee that some permanent reference to the object is maintained. Thus a call might be
anotherStar := new5PointStar(5,aPoint,80.0);
Notice that there is only one class description for S5PointStar, and that it is used to define many objects within the class. In other words, classes are types, and the objects are instances of the type. The application could also save the stars in some collection structure, like an array, so that the stars could be drawn, moved, and eventually destroyed.
Object Oriented Programming (second version) Programming methodology in which the data elements (objects) in the system form the fundamental unit of program decomposition. Objects are described by means of classes. |
Suppose that we have created these two stars, myNewStar and anotherStar. To draw them we would write
myNewStar.draw(hatchPat);
anotherStar.draw(blackPat);
assuming that hatchPat and blackPat were values of type Pattern. These two statements are called messages to the respective objects and in OOP we say that we "send the draw message" to the objects. We also say that the object receives the draw request and then itself executes its own draw method to fulfill the request. This idea, that the objects themselves execute the methods is conceptually very important in object-oriented programming.
To execute a method in a class of an object we give the name of the object, then a period "." and finally the name of one of the methods defined in the class of that object, with any actual parameters that it requires. In this case myNewStar is known by the compiler to be a reference to an object in the class S5PointStar, and that moveTo is one of the class's methods. Therefore the statement myNewStar. moveTo(aPoint) is a legal statement provided aPoint is a valid Point. In this case the statement is called a message, and the message is said to be "sent to the object" myNewStar. It is sent by the code above, but in most cases this code is part of some other method, perhaps of an object of some other class. We say that this other object "sends the message moveTo to the object myNewStar." Since the draw procedure is also a method, executing it also requires sending of a message as in:
myNewStar.draw(clearPat);
A useful mental picture of an object oriented program in operation is that of a graph, where the nodes represent the objects, and the arcs represent messages sent between the objects. The arcs are actually arrows, as messages are unidirectional, with a sender and a receiver. Functional methods, of course, return some result backwards along the arrow. For example, a graphics or CAD/CAM application might have a "window" object that has a reference to a list object. This list object might have references to several "drawable figure objects" The window might send the message "draw" to the list, and the list, in executing the draw method might send the message "draw" to each of the figures. The picture of this is shown in Figure 2.5.
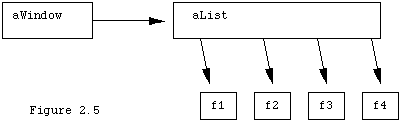
Another possible mental picture would be a slightly different graph, which is much more static in concept. Again the nodes can be objects, but the arrows can represent references to other objects. This is a similar picture to those we have used to illustrate pointer variables. In this scheme we draw arrows between objects when some class has an indirect instance variable of a class type. In S5PointStar, the fLocation instance variable, whose type is Point, is just such a case. Such an instance variable is a "reference" to the other object, and it is represented by an arrow in this picture. At run time, the instance variable contains a reference to some actual object of the necessary type. Actually, since the reason for maintaining a reference to another object is to send it messages, the two pictures are almost always the same. In the above case the arrows do represent messages ("draw") sent and they also represent instance variables, as a window has an instance variable of type Lists.T, which we shall define in Chapter 4. Sometimes we say that a window contains a list, when in fact we mean that it has an instance variable of type Lists.T, which means that we really contain a reference to a list.
The two pictures may differ however, as it is possible to have global variables that refer to objects, and it is possible to use these global names to send messages to those objects. Therefore, if our list above was a global object (unlikely) and we send it a message "draw," we will get the picture in Figure 2.5, but the static picture would not contain the arrow from aWindow to aList.
When programming in Modula-3, the end result is very similar to the end result in Pascal or Modula-2. A program consists of a collection of declarations and a "main" block. The major difference is that most of the important variables in the Modula-3 program refer to objects rather than to elementary data. Also, there are usually only a few statements in the main block of the program. These few statements generally create a master object that controls the behavior of the entire program. For the most part the only place in which we use elementary data items, like integers or chars, is for the fields, or instance variables, of the various objects in the system. Note that the instance variables may be of any type, including class types. They may even have the same class type as the type being defined.
Generally speaking, we shall declare our classes in interface files intended to be IMPORTed by other interface files that have need of the services provided by a class as well as being IMPORTed into modules. We shall often declare several closely related classes within the same interface, but we shall not declare unrelated classes within the same interface. An interface file therefore corresponds to an Abstract Data Type and the classes that it defines correspond to the data abstractions that make up the ADT. We thus employ two levels of packaging within our programming, the interface level and the class level. This packaging of related things is called "data encapsulation." Modula-3 actually employs various encapsulation, or packaging, mechanisms, and these permit us to match our ideas or abstractions to our programs. For example the Modula-3 keywords "PROCEDURE" and "END" are used to package a group of declarations and executable statements. Likewise "RECORD" and "END" encapsulate a record.
Decomposing into interfaces also permits various details of the definition of a class to be hidden from clients. These details are not in the public interfaces at all, but in an associated private interface file, which we will discuss in Section 2.10. They might also be in the associated module file. This makes it easier for implementors of server modules to make changes and know that clients have not made effective use of assumptions about the implementation. Thus, we may change details of the imlementation without requiring any change in the clients. This idea is called "information hiding" and it is a very important way to guarantee that clients do not contain code that restricts the service providers. This makes it possible to create programs in which the parts are relatively independent of one another, which makes changes and maintenance easier. This is so because fewer relationships between parts means that fewer things need to be examined to discover the effect of a change, and also fits better with our limitations on remembering detail. If information hiding is employed then it becomes harder to write software in which an error in one piece will only be apparent in the failure of some other seemingly unrelated piece. It is an important way to improve the quality and understandability of our software.
To give a specific example, the library developed for this book consists of about 90 classes. These are defined in about 45 public interface files with names like Object.i3, Lists.i3, and BinaryTree.i3. The private details of most classes are given in corresponding private interfaces files: PRObject.i3, PRLists.i3, and PRBinaryTree.i3. The methods of the classes declared in the interfaces are all defined in separate module files such as Object.m3, Lists.m3, etc. Therefore, in addition to the main program file, main.m3, which is generally quite small, there are about 125 other files that are used in one way or another to add functionality to our programs. This is, of course, in addition to the many files that are "built-in" to the Modula-3 system such as "Wr.i3" and "Fmt.i3".
As said above, there are two tasks to programming: design of the program text (writing the program) and design of the run time behavior (defining what the program does). The latter task is fundamental and is the place to begin. That is to say, we design the objects and their behavior, and then write down descriptions of them. These descriptions are the classes. To first discover the objects, it is useful to look carefully at the problem to be solved, searching for components of the "real world" system that interact with other elements or are acted upon by other elements. If we think of the system to be modeled as one containing actors who provide services and require services then we may model these actors as objects. Then we must consider how the actors are to be grouped. Usually this is by function: actors of the same kind are those that provide the same or similar services. Once we have some idea of the basic actors, it is also useful to think in terms of generalization/ specialization of these functions. It may be that we can think of a large class of actors/ objects as being specializations of a single generalized type.
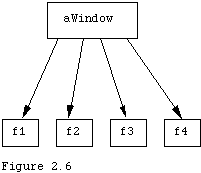
Once we have an idea of what the objects are to be we must actually design them. One way to design the objects is to draw the message graphs that we indicated above. A first attempt at a graphics application might result in the picture shown in Figure 2.6. When we realize that there will be a variable number of figures drawn in the window, and that we might want to segregate them into separate groupings, we might refine the picture to the one shown previously, in Figure 2.5.
We might also expand the picture so that there are several windows, each with separate figures to be drawn within each window.
Next we would discover that the figures all share some things in common since they can be drawn, like our five point stars shown earlier. They have differences as well, such as shape, rectangles having a different shape than five point stars, for example. Therefore we decide that we will want a class, Figure, to define the common parts of all of the drawable figures, as well as a Window class, and a List class. The main idea is that the objects needed in the system lead us to design classes that describe those objects.
The differences between objects lead us to organize the classes in a certain way. It is a special feature of object oriented systems that the classes are related to one another and the relationship is one of a more general class to a more specific one. In most object oriented languages, the relationships are defined in a static way, within the compiler, though there are languages in which the relationships are dynamic and may be changed as the program executes. In Modula-3, the classes form a tree, with each class except ROOT having one parent class. As the name implies, ROOT is the top or ultimate parent in the class Hierarchy. The fundamental idea of the parent-child relationship in this structure is that of a generalization-specialization hierarchy, with the parent being more general and the child being more specialized. (A child class is sometimes also called a derived class.)
Parent Class A class that is used as the parent in inheritance. The child class is sometimes called a derived class. |
Child Class A class that is a subclass of the other class |
In the current example, we have indicated that we want a parent class, Figure, which defines common properties of the drawable figures. Appropriate subclasses of this class would be Rectangle, and S5PointStar. This leads us to another picture of our system, one which is completely static, and that shows the relationships between classes. The root of the class hierarchy is the abstract class "ROOT" which is built in to Modula-3. ROOT is a subtype of REFANY, the general pointer type. We shall create a class Object.T to fulfill the function of a local root of our class library. In this view our system might look (in part) like Figure 2.7. Object.T is actually a subclass of ROOT, though we don't show that here.
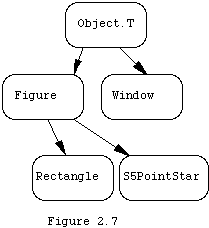
The concept of defining a class by giving only those features by which it differs from another class is called "inheritance," and Modula-3 has what is called "single inheritance" as a class may have only one parent class from which it is derived. Note, however, that a class actually inherits from all of its ancestors in the inheritance tree. The parent class is also often called a super class,. Therefore our inheritance structure is treelike, with a single root.
The idea of inheritance as defining a generalization-specialization hierarchy has a very specific meaning. In any context in which an object of a class may be used, an object of any subclass may be substituted. Therefore, if fig1 is a variable defined to reference an object of type Figure, and aRect is a Rectangle, then the assignment fig1 := aRect; is legal. It is legal because Rectangle is a subclass of Figure.
Type Specialization Principle In any context in which an object of a given class may be used, any object of a subclass may be substituted. |
The (public) definition of Figure might itself look like:
TYPE
Figure = OBJECT
fLocation: Point;
METHODS
draw(fill: Pattern);
END;
S5PointStar = Figure OBJECT
fDiameter: REAL;
fImbalance: INTEGER;
METHODS
init5PointStar(imbalance: INTEGER; Loc: Point; Diam: REAL): S5PointStar;
moveTo(newLocation: Point);
END;
Inheritance is thus both an organizational principle of object oriented programming and a technique to make the life of a programmer simpler and more disciplined. Once some functionality has been created and tested, we may use that functionality as part of a new system, more specialized than the one from which it inherits. It is from this that object oriented programming draws much of its power.
Object Oriented Programming (final version) Programming methodology in which the data elements (objects) in the system form the fundamental unit of program decomposition. Objects are described by means of classes. Classes are developed by means of successive refinement using inheritance. |
We can actually use inheritance to improve our design of S5PointStar in another way. There are a few problems with our declaration of S5PointStar. First is that we have not yet shown a way for the actual method implementations to be associated with the method headers given in the class declaration. A slightly improved declaration is given below, in which we do indicate the actual methods.
TYPE
S5PointStar = Figure OBJECT
fDiameter: REAL;
fImbalance: INTEGER;
METHODS
init5PointStar(imbalance: INTEGER; Loc: Point; Diam: REAL): S5PointStar
:= Init;
moveTo(newLocation: Point) := MoveTo;
OVERRIDES
draw := Draw;
END;
These method assignments are assignments of actual procedures to the methods of the class. We must then define these procedures, though you will immediately notice something unusual when we do this.
PROCEDURE Init(self:S5PointStar; imbalance: INTEGER; Loc: Point; Diam: REAL) =
BEGIN
self.fImbalance := imbalance;
self.fLocation := Loc;
self.fDiameter := Diam;
END Init;
Notice that the actual procedure to be executed when the method is used has an extra parameter of the type of the class of which it is a method; here S5PointStar. This extra variable is the way that each object knows "itself" when it is executing the method. We shall always use the name "self" for this parameter to indicate this. This parameter is needed so that the object executing the method can perform other operations on its own instance variables and have access to its own methods.
The second major flaw in our declaration of S5PointStar is that it leaves its implementation open to those programs that want to use it. In other words, the instance variables can be directly changed by a client program without using the methods of the class. For example, the class provides a method named moveTo to modify the fLocation instance variable, but a user could modify it using an assignment such as
myNewStar.fLocation := aPoint;
This is very undesirable, since there are situations in which the internal consistency of an object can be destroyed by such operations. Therefore, we would like to make it possible for the designer of a class to protect such details of the implementation from casual changes. This is called "information hiding." Our means of doing this in Modula-3 is to split the declaration of the 5 point star class into two separate classes, one that shows only the publicly available information (usually just methods) and the other that gives the rest of the details. These two classes will be defined in separate interface files, so that the designer has a way to prevent their access by limiting access to the interfaces themselves. For example the public interface for a five point star could be something like:
INTERFACE Stars
FROM Figures IMPORT Figure;
FROM Patterns IMPORT Pattern;
FROM Points IMPORT Point;
TYPE
S5PointStar <: PublicStar;
PublicStar = Figure OBJECT
METHODS
moveTo(newLocation: Point);
END;
PROCEDURE New(imbalance: INTEGER; Loc: Point; Diam: REAL):S5PointStar;
END Stars.
This interface indicates that S5PointStar is a subclass of type PublicStar, but otherwise gives no information about it. However we know that we will inherit draw and moveTo methods from PublicStar. S5PointStar inherits draw from PublicStar since PublicStar inherits it from Figure. We also have the declaration of the generator function, New, here, so by importing this interface, we may create, draw, and move five point stars. We may not directly execute the initialization, but that is done within New anyway. Nor may we manipulate any instance variables, since we don't have access to them via this interface.
We now need another interface file for the rest of the details of this class.
INTERFACE PrivateStars;
IMPORT Stars;
FROM Points IMPORT Point;
FROM Patterns IMPORT Pattern;
REVEAL
Stars.S5PointStar = Stars.PublicStar BRANDED OBJECT
fDiameter: REAL;
fImbalance: INTEGER;
METHODS
init5PointStar(imbalance: INTEGER; Loc: Point; Diam: REAL): Stars.S5PointStar
:= Init;
OVERRIDES
draw := Draw;
moveTo := MoveTo;
END;
PROCEDURE Init(self:Stars.S5PointStar; imbalance: INTEGER;
Loc: Point; Diam: REAL):Stars.S5PointStar;
PROCEDURE Draw(self:Stars.S5PointStar; fill: Pattern);
PROCEDURE MoveTo(self:Stars.S5PointStar; newLocation: Point);
END PrivateStars.
This interface first imports the public interface, Stars, so it has access to the names declared there. We must use qualified references to the items declared in Stars, however. PrivateStars then reveals the real declaration of Stars.S5PointStar as a BRANDED subclass of Stars.PublicStar. This branding is necessary in revelations so that the system can distinguish between types that may be structurally identical, but which we must keep distinct. Here we also introduce the remaining instance variables and the initialization method. The inherited methods are to be given procedure bodies here, so we include them in the OVERRIDES section of the declaration, marking them with the actual procedures to be used. After the declaration, we give procedure headers for the methods of this class, so that they will all be defined. The final part we need to complete this class is the MODULE file, which gives the implementation of all of the methods. Here, we only indicate its structure. Note that it EXPORTS both the public and private interfaces.
MODULE Stars
EXPORTS Stars, PrivateStars;
PROCEDURE Init(self:S5PointStar; imbalance: INTEGER; Loc: Point; Diam: REAL): S5PointStar =
BEGIN
self.fImbalance := imbalance;
self.fLocation := Loc;
self.fDiameter := Diam;
END Init;
...
BEGIN
END Stars.
Finally, we note that when building a subclass of a class defined with both a private and a public interface, the interface and module defining the new class will often need to import both the public and the private interfaces of the parent class. This is because the details of the parent are hidden in the private interface, and the new class will almost always need to use these details in some way--especially in implementing the new methods and the override methods.
The basic rule of object oriented design is to "design the objects." This means to think of your program or system as a collection of interacting objects able to communicate with each other by sending messages. Each "kind of object" (class) generally provides a single service or simple functionality (objects are simple). The methods of a single object tell its clients what services it provides and they provide a means for the clients to request the services because the method names are names of the services. If we were designing a robot in an object oriented way we would have classes corresponding to its various parts, such as sensor, gripper, walker, memory, and controller. We would have specializations of most of these classes since there are different kinds of sensors and controllers. The memory would also have several parts, including as a stack for remembering where the robot had been. Our design process would consider the uses of the robot, and therefore the needed functionalities and therefore the needed parts. These parts would be the objects, and the types or kinds of objects would become the classes. The generalization/ specialization of the kinds of objects helps us to discover the classes.
We design the classes by designing procedure headers for the services that the classes must provide and also (somewhat later) by designing the actual implementation of the local state variables that the objects of the class must maintain in order to provide the services. Here it is useful to think about the "parts" out of which we can build an object in the class. A robot "has" sensors, actuators, etc. Often an object is composed of parts that are objects of different classes. Sometimes the parts are elementary data items such as integers and ordinary arrays. This phase, programming the classes by composition of parts, comes after the analysis of the services and the design of the prototypes of the functions that will implement the services of the class, however.
One possible difficulty with this approach is that while classes are defined from the top down in any system using inheritance, they are usually discovered from the bottom up, or even from the middle out. Therefore the design process and the programming (writing down of a program) process do not follow the same path. One aid in designing the classes is a pack of 3-by-5 cards on which we write down the characteristics of our classes . The front of each card might look like:
The responsibilities describe the service that the class is to provide to other classes. The collaborators are other classes that are needed by this one, or are associated with it, and whose services it requires in turn. Here we write down what each class is responsible for, and what other classes may be used to assist it. The main responsibility of our Window class is to maintain a drawing port and to manage the objects drawn in that port. Its main collaborator is a list to keep track of the drawn objects.
The back of the card could be:
Here we are more specific, and only fill this in when we have taken some time to consider the class responsibilities. The methods define the services that the class provides, which are certainly chief among its responsibilities. The instance variables define the static information that objects in the class need to carry out class responsibilities: they form the internal representation of the object. To design a class we design methods to carry out the services and we design instance variables, the representation, based on the frequency with which certain services will be used. The idea is that we choose a representation so as to make frequently used services efficient. In the current example, since a Window provides a drawing environment, it will need a draw method and, perhaps, a graphPort instance variable. These cards are called CRC cards, which means CLASS/ RESPONSIBILITY/ COLLABORATION.
CRC cards are useful because they permit "brainstorm" thinking, shuffling, and dealing out into various geometric configurations to demonstrate different relationships. They are also disposable so that ideas that don't bear fruit may be easily discarded. CRC cards were introduced by Kent Beck and Ward Cunningham at the 1989 OOPSLA conference. See the bibliography.
The following declaration represents the public part of a class of bounded stacks of real numbers. The design of it could be greatly improved, but we have tried to make it as close to the definition given earlier as we could.
The CRC cards for this class might look like Figures 2.10 and 2.11. Of course these would have been created as part of our design process for the class, and would therefore exist before any of the above code.
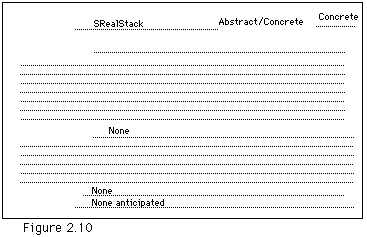
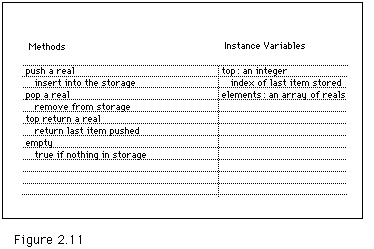
The class developed from these cards is shown below. Note the differences between this declaration and the original SimpleStack.T or LinkedStack.T declarations, which used the more standard Pascal/Modula-2 style. First, the declarations of the procedures and functions (methods) used to manipulate these stacks are within the declaration of the stack type itself. This is called "encapsulation" of the methods within the data type. Next, notice that we do not need to name a stack as a parameter to our methods. A message naming a method will be sent to some particular stack, and this stack, the receiver of the message, will be the one on whom the push or pop is done.
TYPE
RealStack <: Public;
Public = OBJECT
METHODS
push (E: REAL);
pop (VAR E: REAL);
empty(): BOOLEAN;
top(VAR E: REAL);
END;
PROCEDURE New():RealStack;
REVEAL
RealStack = Public BRANDED OBJECT
fElements: ARRAY [0..99] OF REAL;
fTop: INTEGER;
METHODS
initStack():RealStack := InitStack;
OVERRIDES
push := Push;
pop := Pop;
empty := Empty;
top := Top;
END;
PROCEDURE InitStack(self: RealStack):RealStack;
PROCEDURE Push(self: RealStack; E: REAL);
PROCEDURE Pop(self: RealStack; VAR E: REAL);
PROCEDURE Empty(self: RealStack);
PROCEDURE Top(self: RealStack; VAR E: REAL);
Notice that between the keyword OBJECT and the keyword METHODS, we have declared two data items, called "instance variables" fTop and fElements, and between METHODS and END we define or override one private and four public methods. This is perhaps the most easily recognized feature of object oriented programming: the functions are bound up in the declarations of the data. This is more than just a notational convenience, however. These methods are the only means of operating on the data which is actually hidden.
In some ways a class declares things that are very much like records. The difference between the ordinary RECORDS of Pascal and the classes of Modula-3 is that we can use the latter as a mechanism for encapsulating procedural elements as well as data elements.
Usually all of the instance variables and often some of the methods of a class are are hidden in the private interface. The client should not be able to manipulate the implementation for at least two reasons. First, the client could make it impossible to guarantee that the service is provided correctly. Imagine a stack service in which any code can manipulate the top of the stack. It would be hard for the stack to guarantee that items were produced in a last-in first-out manner. The second reason for wishing to hide implementation information is that there are times that the implementation must change after the clients have been written. Sometimes this is for reasons of efficiency, and sometimes it is because the problem we are trying to solve has changed slightly. In either case, if the clients have access to only a procedural interface to the information then the variables out of which the implementation is built can change and often the declarations of the procedures that the clients use will not need to change. This means that the clients do not need to be rewritten. They may not even need to be recompiled. If they have access to the variables, then, when the implementation changes and the variables of the old implementation disappear, any client using the variable will need to be redone, perhaps drastically. This drives the cost of modifying software up dramatically.
Information Hiding Principle Details of the implementation of a data type should not be accessible to clients of that data type. |
Also notice that there is a separate function declaration New that is associated with the class and defined in the public interrface. This function is an object generator. This generator function of RealStack is intended to be the way that we actually create stacks of this type. In fact it is intended that calling this function be the only way to generate a new stack. Given these declarations we could declare variables of the type in the usual way.
myStack: RealStack ;
MyStack is a reference variable. It refers to an object in class RealStack. We may also create an actual real stack and save a reference to it using a call to the generator.
myStack := newRealStack();
myStack.push(6.234);
myStack.pop(X);
IF myStack.empty() THEN
Wr.PutText(Stdio.stdout, "Empty.");
END;
If this class were to be actually implemented (it won't be, but an improvement of it will), then we would put the above type declaration, and the declaration of the generator into the two interface files. The original declaration belongs in a public interface along with the generator, and the revelation. The procedure headers for the method implementations goes in the private interface. In the module part or ".m3 file" we would need to define all of the methods of real stacks. When we define a method of a class we must give it a first parameter, usually named self, of the type of the class of which it is a method. Therefore when we define empty() of class RealStack, we will need to declare it PRocedure Empty(self: RealStack). Look at the procedures definitions shown below.
PROCEDURE Empty(self: RealStack) =
BEGIN
RETURN self.fTop < 0;
END Empty;
PROCEDURE Push(self: RealStack; E: REAL) =
BEGIN
IF self.fTop < 99 THEN
INC(self.fTop);
self.fElements[self.fTop] := E;
END;
END Push;
The implementation part will also need to define the generator function New that was declared in the public interface part. Generators follow a pattern which is exhibited by this example:
PROCEDURE New(): RealStack =
VAR result: RealStack;
BEGIN
result := NEW(RealStack);
Object.FailNil(result);
EVAL self.initStack();
RETURN result;
END New;
Given the descriptions above of Abstract Data Types and of Object Oriented Programming in Modula-3, it is easy to describe a scheme for melding the two into a strategy for implementation. Data abstractions are modeled as classes. A collection of data abstractions making up an Abstract Data Type form a pair of interface files and an implementation (module) file. The public interface portion contains the class definitions and should also contain (or at least refer to) documentation giving the rules of the ADT. Thus a public interface forms a specification of an ADT. The private interface portion gives the instance variables and any private methods that are not intended for users of the service provided by the class.
A strength of Modula-3 is that the details (names and types) of the instance variables implementing each class may also be hidden in the private interface. These are really internal items, so we want to be possible to prevent clients from directly manipulating them. A program importing the public interface and declaring a RealStack named stack, will not be able to make reference to the instance variable stack.fTop. This variable is private to the stack itself. We may refer to the field from the methods of a class that inherits RealStack, however, because such a class will be given access to the private interface file.
If an ADT is derived from another then the interface implementing the derived ADT will IMPORT the interface of the ADT it is derived from. If the derivation is a specialization then the classes implementing the data abstractions will be subclasses of classes in the ADT it is derived from.
Object oriented programming using reference variables in Modula-3 requires that a programmer will adopt a certain mental model, or set of ideas, about the nature of the computational system that she or he is using. In many ways this system is similar to the model used in standard C or Pascal, but its differences are important. Rather than thinking of a single computing mechanism (CPU) with a single memory, it is useful to think of a single processor and many memories. Each object in the system should be thought of as having its own memory. In fact, the most useful model considers each object to be composed of four parts: memory, process, sensor, and effector. (See Figure 2.12.) An object sends messages to other objects using its effector. This is just an outward directed communication channel. Likewise it receives messages through its sensor.
Within the methods of a class, the receiver of a message (who must be in the class of the method), is referred to by the identifier "self," which we use as the name of the first parameter in method implementations. The model of execution is that the object itself executes the method (rather than a "computer" executing a procedure). The object currently in control is the object executing the method. It knows "itself" by the name self provided that this is the name we use for the distinguished first parameter of the method implementation procedures. Therefore within a method of RealStack, a procedure or other message may be called, and the object "self," which is executing, may pass itself to that other procedure or method using the reference variable self.
self The object which currently has control of the processor is known as "self." When a message is sent to another object, then that object becomes "self" while it executes a method in fulfillment of the message. |
When an object receives a message via its sensor, it matches the message with some method in its own process part. It then executes that method. As a consequence of executing the method it may change some values in its memory part and it may also use its effector part to send messages to other objects, or even to itself. Thus a system in execution might be depicted statically with a picture like Figure 2.13. Here we have several objects in the system. The arrows indicate messages that have been sent at some time.
We might refine this picture to give it a more dynamic element, which is really the case in a program in execution. Recall that our model has only a single processor, or CPU. At any given time some object in our system has control of this processor. Suppose we indicate the object with control using a filled oval as in Figure 2.14.
When the object in control sends a message to another object, it passes control of the CPU along the message path to the other object. This might leave us in the situation of Figure 2.15.
Eventually, all messages directly and indirectly sent because of our sending the message that just took us from Figure 2.14 to Figure 2.15 would complete. At this point the processor would be passed back along the message path and we would again be in the situation of Figure 2.14. However, each of the objects that received messages as a result of this one message send have had control of the CPU, have executed methods, and have, perhaps, changed their own memory variables as a result. Notice that a simple modification of this model would permit there to be several CPU's. Therefore, the object programming model can be used as a simple way of thinking about parallel programs.
A slightly more accurate picture of a single object is shown in Figure 2.16. Here we indicate a possible implementation of objects. The effector part is nothing more than the presence of instance variables in an object whose types are class types. Here we indicate two such variables, though there could be any number of them. An object gets access to another object, enabling it to send messages to that other, by maintaining a reference to it. Therefore the effector is, in reality, just part of the memory. The memory may also have values that are not references to other objects. These values might be integers ,or arrays, or whatever else is appropriate to the class of the object.
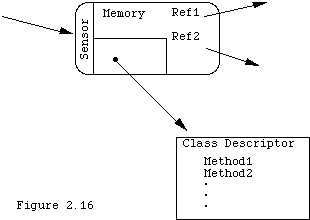
An object gets access to its process part by maintaining a reference to a class descriptor stored in the running computer. This descriptor contains all of the methods defined in a given class. When an object is created within a class it is given a reference to this descriptor and it can never change it. Thus, an object, once created within a class, is always a member of that same class. Inheritance is implemented by also giving each class descriptor a reference to the descriptor of the parent class of the given class. Therefore, an object has a way to get access to the methods of its own class, as well as the methods of ancestor classes.
In the next chapter we shall take these ideas much deeper.
Procedural abstraction permits us to encapsulate processes, name them, parameterize them, and then ignore the details of their implementation. It is an important technique and forms the basis of some software development methodologies. It is an important secondary technique of object oriented programming.
The technique of data abstraction permits us to encapsulate data, define their properties and their actions, and then ignore the details of their implementation. It is the fundamental decomposition technique of object oriented programming. Object oriented programs are designed by designing the data that they use and giving actions to the data.
A data abstraction is a description of a collection of objects and the properties and behaviors of those objects. An abstract data type (ADT) is a set of interacting data abstractions with one of them primary. If an ADT provides more than one data abstraction then the primary one usually obtains services from the others.
In object oriented programming we use a class to describe a data abstraction. As such, it is a description of the data objects that conform to that description. The description specifies the components of the data (instance variables) as well as the behaviors (methods). Classes also provide a visibility mechanism by which interfaces of objects may be separated from implementation details.
Classes are organized into a specialization structure with parent classes describing part of the structure of child classes, and child classes extending and specializing the capabilities of the parent classes.
Objects in Modula-3 are referred to indirectly (by means of reference variables). The use of reference variables permits decisions about which method to be executed in fulfillment of a message to be delayed until runtime, increasing flexibility.
The model of programming in object oriented languages is one of autonomous objects that communicate by sending messages to each other. These messages request services of the target of the message. Control of a computation follows the path of messages, so that at any given time some object has control of the computation, hence of the computer on which it runs.
1. (2.5) Build and test a linked list implementation of the class RealStack similar to the ordinary implementation discussed in section 2.5. Put the type declarations in the interface files RStack.i3 and PRRStack.i3. Put the implementations of all of the methods in the file RStack.m3. Build a separate main Module that will exercise the package. The next fields of each object should be of type RealStack. Note that it IS legal to have an instance variable of the same type as the class type that contains it. Omit the call to FailNil unless you implement such an ordinary procedure yourself. When called, FailNil checks its parameter and if that is NIL it should print an informative message and then halt the program.
2. (2.5) A fundamental problem with the stack class of problem 2.1 is that a stack as a whole is represented in the same way as a "node" in the stack. Improve on this in the following way. Rename the stack class from problem 2.1 to be StackNode. (Use the editor to change all occurrences of RealStack to StackNode. ) Now build another class RealStack whose single instance variable is a StackNode. Now an object of this new class represents the stack as a whole and the StackNode class represents the nodes out of which we build a stack. You now have an ADT with two data abstractions.
3. (2.5) Design test data to test our implementation of LinkedStack.T. You should have one or more tests for each of the rules in the definition of a stack. For example, the rule that states that empty must return true immediately after initialization can be easily checked by creating a stack and immediately calling empty.
4. (2.5) Give rules defining a bounded stack similar to those we gave for a stack. Verify that our first implementation of SimpleStack.T (Section 1.5.11) obeys your rules or show specifically how it does not. It will be helpful to add a predicate FULL to the data abstraction to decide at run time if a given bounded stack is full.
5. (2.9) What is it about the information hiding principle that, when it is used, makes it easier to modify existing software? Is there anything about it that makes it harder to modify existing software? How is information hiding related to the "rule of seven" discussed in the last chapter?
6. (2.10) What is it about inheritance that might make it possible to build software faster? What is it about inheritance that might make it possible to build better (fewer bugs) software?
7. (2.11) Build and test the RealStack class as discussed in section 2.11. Put the type declarations in the interface files RealStaA.i3 and PRRealStaA.i3. Put the implementations of all of the methods in the file RealStaA.m3. Build a separate test module that will exercise the package. Omit the call to FailNil unless you implement such an ordinary procedure yourself. It should print its parameter string and then halt the program.
7. (2.11) Pick a board game such as checkers or chess with which you are familiar. Suppose that you wanted to write a program that would take the part of one player of the game, and which would also manage the board and game pieces, showing the state of the game (board and positions of the game pieces...) on the screen. Name three or four likely candidates for classes that you would consider when designing this program. For each of them, give a few methods. Which of these methods will need to request services from objects in one of the other classes? Add additional methods to those classes, if necessary, to represent those services. Create CRC cards for your design up to this point.