Lovliest vision far Of all Olympus' faded hierarchy!
All the better; their fraction is more our wish than their faction: but it was
a strong composure a fool could disunite.
Shakespeare, Trolius and Cressida
This was a merry message.
Shakespeare, Henry V
In this chapter and the two which follow, we shall lay the foundation for the development and use of a large software library of general purpose tools that may be used in virtually any development project to shorten development time and help guarantee correctness of the code. We shall describe a number of "Classes" of "objects" arranged into "compilation units" which may be IMPORTED by programs or other compilation units and classes. Later chapters describe the implementation of the classes. In Chapter 5 we will show two examples of the use of the classes: to create deterministic finite state automata simulators, and to show a simple translator from infix expressions to postfix.
In object oriented programming a running program is a collection of communicating objects which carry out the computation task collectively by requesting services from and providing services to other objects in the system. The objects are usually thought of as having a form of independent existence and a large degree of autonomy. An object is more than just a block of data like a record. One object, or a procedure or a program block (called a "client") is generally not permitted to modify another object. It is only permitted to request service from the object by sending it a message naming the service required. The object receiving the message interprets it as appropriate and then fulfills the service request if possible by executing a method using parameters provided by the client.
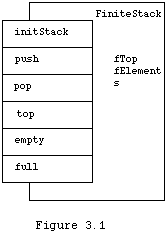
To solidify these ideas, here is the declaration of a Class called FiniteStack.T. From this point on we will be using a naming convention that is useful in practice. All class names will be defined in interfaces whose name is a capitalized noun descriptive of the main class exported by the interface (e.g. FiniteStack). The main class itself will always be called just T (for TYPE). When we are writing code outside of this interface (and its implementation) we shall refer to the class using the interface name followed by ".T" as in FiniteStack.T. All instance variables (field) names will begin with the initial letter f, followed by a noun descriptive of the concept modeled by the variable. all method names will begin with a lower case letter. This convention helps class names, methods, and instance variable names stand out in certain contexts. Methods which are functions have names which are nouns or short noun phrases which describe the returned result. Procedural methods have names which are verbs or verb phrases describing what the procedure does. One exception is for function that return a Boolean result. These are given names that are adjectives, describing the condition that they test. Note also that abbreviations are seldom used, that capitalization is consistent, and that when two words are catenated to form a compound word, the first letter of the second and subsequent word is capitalized as in FiniteStack. The following declaration is an improvement on the declarations at the end of the last chapter, but it is possible to improve it further. See the exercises for hints. The following declarations would be put into a file named FiniteStack.i3. If your operating systems is unable to use names longer than 8 characters, the name of the file may need to be truncated or otherwise modified. In any case, the filename is intended to name the principal type of the interface.
INTERFACE FiniteStack;
IMPORT Object;
CONST FiniteStackMax = 20;
TYPE
T = Object.T OBJECT
fTop: INTEGER:
fElements: ARRAY [0.. FiniteStackMax-1] OF REFANY;
METHODS
initStack() := InitStack;
(* Initialize a newly created stack. Leaves it empty.*)
push(o: REFANY) := Push;
(* Insert d into the storage. No op if the structure is full. *)
pop() := Pop;
(* Remove the most recently inserted object. No Op if empty. *)
top(): REFANY := Top;
(* Return a reference to the last object inserted into the storage. *)
empty(): BOOLEAN := Empty;
(* True if there are no objects in storage. *)
full(): BOOLEAN := Full;
(* True if there is no room for additional objects to be stored. *)
END;
PROCEDURE InitStack(self: T): T ;
PROCEDURE Push(self: T; o: REFANY) ;
PROCEDURE Pop(self: T)
PROCEDURE Top(self: T): REFANY ;
PROCEDURE Empty(self: T): BOOLEAN ;
PROCEDURE Full(self: T): BOOLEAN ;
PROCEDURE New(): T;
(* Objects are inserted into the finite stack using push. They are removed
and retrieved with pop and top respectively. The behavior is last in-first
out (LIFO), meaning that the most recently pushed object will be the next
popped. NIL will be returned if the client attempts to pop an empty finite
stack, and attempting to push onto a full one results in no operation (no-op)
FORMAL RULES
1. Initialization must be done once for any stack object.
This is done correctly by FiniteStack.New.
2. Immediately after initialization, empty returns true and full
returns false. Pop is illegal and results in no-op, and top, while
also illegal, returns NIL.
3. Immediately after push, empty returns false and full may return true.
4. If full would return true then push is illegal and results in a no-op.
However if push fails to insert X by reason of executing when full is
true, the stack may not properly be LIFO.
6. FiniteStack.New returns a new allocated and initialized (empty) stack.
7. At most some fixed finite number (FiniteStackMax ) elements
may be stored at any time. If the stack currently holds
FiniteStackMax elements then full returns true.
*)
END FiniteStack.
We illustrate the above declaration with the Class Photo, shown in Figure 3.1, which indicates that the methods are to be public, and the instance variables, enclosed within the boundary, are to be private.

Having made the above declaration, we may want a finite stack object called ExpressionStack from class FiniteStack to be available when the program executes. Usually we will want to refer to this object indirectly using a pointer. Therefore the declaration would be
VAR ExpressionStack: FiniteStack.T;
The variable ExpressionStack is called a reference variable because it is used to refer indirectly to an object within some class. Its actual value will not automatically be an object, however. This declaration states that ExpressionStack is to be an object, but a declaration alone is not quite enough to create the ExpressionStack. Objects are created dynamically at run-time, so in some code block in which the above declarations are visible we will need to execute:
ExpressionStack := FiniteStack.New();
Now the ExpressionStack is a properly created object and available for providing services like push, top, and pop. The generator, FiniteStack.New is shown below. This and the method definitions will appear in the implementation file associated with the finite stack interface file. This file will be named FiniteStack.m3. It will begin with a heading indicating the module name and list any necessary imports. Likewise it will end with a statement block (here empty), followed by the module name and a period. The initialization method initStack is also shown below. It merely guarantees that the stack is empty.
MODULE FiniteStack
EXPORTS FiniteStack;
IMPORT Object;
PROCEDURE New(): T =
VAR result: T;
BEGIN
result := NEW(T);
Object.FailNil(result);
EVAL result.initStack();
RETURN result;
END New;
PROCEDURE InitStack(self: T) =
self.fTop := -1;
END InitStack;
...
BEGIN
END FiniteStack.
Because safe creation of an object depends on executing both the call to the standard NEW routine,checking that the call succeeded, and also executing some initialization routine, we always include one or more object generator functions, which return properly initialized instances of the associated class. Note that it calls ordinary procedures NEW and Object.FailNil. It then sends the result variable the initialization message. Since this method is a function, however, we execute it in an EVAL statement, since we don't need the returned value, which is actually the same object as result itself. This procedure New may be taken as a template for the creation of generator functions in all of our classes. The only difference is the specific initialization method employed.
We then perform safe creation and initialization of the reference variable expressionStack simply with
ExpressionStack := FiniteStack.New();
Generator An function that returns a newly created and initialized object in some class. Sometimes this is an ordinary function, and sometimes it is a method of another class. In this library objects are always created with generators. |
At some point within a client program, we may wish to push an expression CurrentExpression onto this stack. When ExpressionStack was created its type was declared to be FiniteStack.T so that it had access to the method push. The client then sends the message
ExpressionStack.push(CurrentExpression);
The object will receive this message and will execute its method push, with parameter CurrentExpression. This method, as it is executed by ExpressionStack will modify the internal state of the ExpressionStack object while maintaining the stack protocol. In this case the "instance variable" named fTop will be increased and then used a subscript into the other instance variable, named fElements. The insertion is at location fTop of fElements.
PROCEDURE Push(self: T; o: REFANY) =
BEGIN
IF self.fTop < FiniteStackMax THEN
INC(self.fTop);
self.fElements[self.fTop] := o;
END;
END Push;
Then if this or some other client immediately sends the message
SomeExpression := ExpressionStack.top();
to ExpressionStack it will produce the thing most recently pushed, which here would be CurrentExpression.
PROCEDURE Top(self: T): REFANY =
BEGIN
IF self.fTop > -1 THEN
RETURN self.fElements[self.fTop];
ELSE
RETURN NIL;
END;
END Top;
PROCEDURE Pop(self: T) =
BEGIN
IF self.fTop > -1 THEN
DEC(self.fTop);
END;
END Pop;
We have learned that an object is just a variable whose type is a class type, and that a class is just a type defined by using the OBJECT keyword. We get access to objects using reference variables. The class definition declares instance variables and methods. Some methods are procedures and some are functions which produce a value that can be used in assignment statements or elsewhere. We have not described the interface Object and its main class Object.T, although we have used it to help declare finite stacks. It is defined in the interface file Object.i3. We will describe it below in the section on inheritance.
In object oriented programming it is important to adopt the attitude that the objects are autonomous and responsible for their own behavior. An object behaves by executing a method defined within its class. The instance variables are changed only by the methods, not by other procedures. When a method is executed it is said to be "executed by the object itself." This view is very important to understanding object oriented programming. An object is like an actor whose "part" consists of a few methods. It is given cues (messages) by other actors (objects) and each cue makes it perform (execute a method).
Object Principle
Objects are autonomous actors. They respond to messages by executing methods. The execution of a method may require sending additional messages
Objects are defined by means of Classes. A class describes both the implementation (instance variables) and the interface or protocol (methods) of the objects which belong to it. A class is like a factory because it can create objects according to a plan.
Class Principle
Classes are both collections and descriptions of objects. A class provides a template, or factory, for creation of objects of the same kind.
Within one system we may have several finite stacks, each receiving messages and each executing its own methods. All may belong to the same class. When a finite stack executes push or pop its fTop instance variable will change, but otherwise no change will be made to fTop . This control over changes to fTop will let us guarantee to users of FiniteStack.T that it will indeed behave as a stack, using LIFO protocol. If the clients could modify fTop directly we could not make the guarantee. The finite stack interface file, and the FiniteStack.T type (Class) definition is supposed to be the complete description of the behavior of a finite stack. Only the methods declared are to modify an object in this class.
Unfortunately, the interface shown above does not guarantee that fTop and fElements cannot be modified by clients. After all, they are declared in the same interface as the methods. Therefore, they have the same visibility and access as the methods. This is undesirable and we need a way to prevent clients from making changes that could break the rules. One solution is to break the interface for finite stacks into two interfaces, the first giving the public details and the other filling in the rest. Thus, an improved interface file for finite stacks is as follows.
INTERFACE FiniteStack;
IMPORT Object;
TYPE
T <: Public;
Public = Object.T OBJECT
METHODS
push(o: REFANY);
(* Insert d into the storage. No op if the structure is full. *)
pop();
(* Remove the most recently inserted object. No Op if empty. *)
top(): REFANY;
(* Return a reference to the last object inserted into the storage. *)
empty(): BOOLEAN;
(* True if there are no objects in storage. *)
full(): BOOLEAN;
(* True if there is no room for additional objects to be stored. *)
END;
PROCEDURE New(): T;
(* Objects are inserted into the finite stack using push. They are removed and
retrieved with pop and top respectively. The behavior is last in-first out
(LIFO), meaning that the most recently pushed object will be the next popped.
NIL will be returned if the client attempts to pop an empty finite stack, and
attempting to push onto a full one results in no operation (no-op)
FORMAL RULES
1. Initialization must be done once for any stack object. This is done
correctly by FiniteStack.New.
2. Immediately after initialization, empty returns true and full returns
false. Pop is illegal and results in no-op, and top, while also
illegal, returns NIL.
3. Immediately after push, empty returns false and full may return true.
4. If full would return true then push is illegal and results in a
no-op. However if push fails to insert X by reason of executing
when full is true, the stack may not properly be LIFO.
6. FiniteStack.New returns a new allocated and initialized (empty) stack.
7. At most some fixed finite number (FiniteStackMax ) elements
may be stored at any time. If the stack currently holds
FiniteStackMax elements then full returns true.
*)
END FiniteStack.
Notice now that if a user imports this interface they have no access to fTop or fElements, as they are not shown here. We indicate that the major class FiniteStack.T is a subclass of FiniteStack.Public, which has the protocol shown. If we do not protect the instance variables in such a way then the language will not prohibit clients or others from having both read and write access to them. Thus, using our first definition, a client could, indeed, say
ExpressionStack.fTop = 99;
which would cause a lot of trouble. This really should not be possible, as the creator of FiniteStack should have better control over changes made, as she or he wants to ensure that it behaves in a LIFO manner. Therefore we protect our instance variables .
The additional details are revealed in another interface, which we call PRFiniteStack.i3 (for Private FiniteStack).
INTERFACE PRFiniteStack;
IMPORT Object, FiniteStack;
CONST FiniteStackMax = 20;
REVEAL
FiniteStack.T = FiniteSTack.Public BRANDED OBJECT
fTop: INTEGER:
fElements: ARRAY [0.. FiniteStackMax-1] OF REFANY;
METHODS
initStack() := InitStack;
OVERRIDES
push := Push;
pop := Pop;
top := Top;
empty := Empty;
full := Full;
END;
PROCEDURE InitStack(self: FiniteStack.T): FiniteStack.T ;
PROCEDURE Push(self: FiniteStack.T; o: REFANY) ;
PROCEDURE Pop(self: FiniteStack.T)
PROCEDURE Top(self: FiniteStack.T): REFANY ;
PROCEDURE Empty(self: FiniteStack.T): BOOLEAN ;
PROCEDURE Full(self: FiniteStack.T): BOOLEAN ;
END PRFiniteStack.
An ordinary client will import only FiniteStack and will have access to all of the methods of FiniteStack.Public applied to a FiniteStack.T object returned by FiniteStack.New. The rest of the details are not needed by ordinary clients. Notice that in interface PRFiniteStack we must qualify the names declared in FiniteStack.i3 with the name of that module. This is because the module names differ. When a module EXPORTS a module it doesn't need to use qualified names, but when an interface or module meerely IMPORTs an interface it does need to use qualified names.
The module implementation for finite stacks needs to export both of these interfaces and is shown below. It is stored in file FiniteStack.m3.
MODULE FiniteStack
EXPORTS FiniteStack, PRFiniteStack;
IMPORT Object;
PROCEDURE New(): T =
VAR result: T;
BEGIN
result := NEW(T).initStack();
Object.FailNil(result);
EVAL result.initStack();
RETURN result;
END New;
PROCEDURE InitStack(self: T) =
self.fTop := -1;
END InitStack;
PROCEDURE Push(self: T; o: REFANY) =
BEGIN
IF self.fTop < FiniteStackMax THEN
INC(self.fTop);
self.fElements[self.fTop] := o;
END;
END Push;
PROCEDURE Top(self: T): REFANY =
BEGIN
IF self.fTop > -1 THEN
RETURN self.fElements[self.fTop];
ELSE
RETURN NIL;
END;
END Top;
PROCEDURE Pop(self: T) =
BEGIN
IF self.fTop > -1 THEN
DEC(self.fTop);
END;
END Pop;
PROCEDURE Empty(self: T): BOOLEAN =
BEGIN
RETURN self.fTop <= -1;
END Empty;
PROCEDURE Full(self: T): BOOLEAN =
BEGIN
RETURN self.fTop >= FiniteStackMax;
END Full;
BEGIN
END FiniteStack.
Excerpts from a client program are shown below. We have left out details of the expression class type for simplicity. However it is important that the expression type have REFANY as an super type so that expressions may be pushed onto a stack.
MODULE Main;
IMPORT Object, FiniteStack, Expression;
VAR
expressionStack, auxiliaryStack: FiniteStack.T;
left, right: Expression.T; // left and right operands of an operator
BEGIN
expressionStack := FiniteStack.New();
...
expressionStack.push(left);
...
auxiliaryStack.push(expressionStack.top());
/*push the top of expressionStack onto the auxiliaryStack */
...
right := auxiliaryStack.top();
right.writeIt(Stdio.stdout); //output the expression right
...
END Main;
When we declare a variable to have a class type, we say that it is a reference to an object. Thus expressionStack, used above is a reference to an object. The object itself was created with the call to NEW within FiniteStack.New. Objects are created only in this way. However it is possible to have several variables referencing the same object. For example in the program excerpt shown at the end of the last section it would be perfectly OK to say:
auxiliaryStack := expressionStack;
It is very important to note that this statement does not create a new stack. It simply makes auxiliaryStack reference the same stack that expressionStack does. The names expressionStack and auxiliaryStack are said to be aliases. Then if we use either alias in a push or a pop, the stack that they reference will be affected. If we push using one of the names and top with the other the object just pushed will be retrieved.
There are two very different ideas about what it might mean for two objects to be "the same." On the one hand we might mean that two objects are the same if they have the same type and the instance variables in them have the same values. This is called identity by value, and it is not what we generally want to mean by "sameness." A stronger notion, object identity, holds only when the two objects are, in fact, one and the same. Said another way, if we have two references to objects, we say that they are the same provided that they reference the same object.
This use of references is very important and intimately bound up with our ideas of abstraction and object independence. It is also the normal thing that Pascal or Modula-3 does when you make assignments using variables which have simple types. If counter has integer type then
counter := 0;
...
counter := counter + 1;
first makes counter a reference to an integer 0. Then it makes counter a reference to some other integer, perhaps 1. Importantly, the first statement does not create a new ZERO. Zero is a mathematical concept in the first place, and a bit pattern in the second. We may put a copy of this bit pattern in a new place, but we don't create a new bit pattern or a new integer. The second statement does not change ZERO, and it does not create a new integer. It simply makes counter reference a different integer, one computed from the integer currently referenced.
Notice how different things are when we use Modula-3's structured types, like arrays and records. If scores and backup have the same array type such as ARRAY[1..100] OF CHARACTER then
backup := scores;
does not make backup a reference to the same array that scores references. The entire array is actually copied into the new location, so that we have two arrays that currently contain the same data. If we modify one of them, say with
scores [5] = xxx;
then one of the arrays is changed, but the other is not. Structured types are like little blocks of data that can be moved around and copied and changed from the outside. Simple types don't behave like that and neither do objects. In this regard, and others, objects are more like simple types than like structured types.
There is an important difference, though, between simple types and objects. If an element has a simple type, as 5 is an element of INTEGER, it cannot be changed. Five is five. Variables referencing it can be changed to reference other things but that is different. Five cannot be changed.
Objects can be changed, but ideally they cannot (or at least should not) be changed from the outside. An object can only be changed by sending it a message, using some name that currently references it and the names of one of its methods. Any name that references the object will do. Then if currentScore and lastValue were references to objects then the assignment
lastValue := currentScore;
would produce lastValue as an alias of currentScore, and the assignment
currentScore[5] := xxx;
would be illegal as it is an attempt to directly modify currentScore. Instead we would say
currentScore.atPut(5,xxx);
sending the atPut message to currentScore, and the change would be effective for the object and hence affect all names (variables) that referenced it. Figure 3.2 shows an object and two references ("aName" and "anAlias") by which we may get access to it. These two references are aliases of each other.
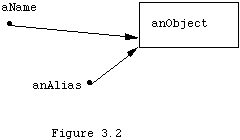
In some way we can think of objects as being "out there", living quiet lives, going about their business. And we can think of variables as being distinct from them but giving us a handle by which we can send them messages. They will respond to our messages, changing their state or behavior, but not disrupting it, we hope.
In a certain way objects are like people. People are distinct from their names, may have several names (aliases), respond to messages, are not directly modified from without, and they provide and require services.
Programming with aliases may take a bit of getting used to and there are some problems associated with it. For example, it is possible to create aliases without the knowledge of a client. Then when a change is made using one alias, the change will show up when using the other, and this will be a surprise if you thought a new object was created rather than an alias. There are many conceptual advantages of aliases however, and this is the reason that they have become a fundamental technique in object oriented programming.
For example, suppose we consider the expressionStack again, and suppose the "expressions" we push onto the stack are actually arithmetic expressions as we use in algebra. Also suppose that such expressions have a method simplify which they use to simplify themselves. The operation of the method changes the internal state of an expression object so that its new representation is an algebraic simplification of its former representation. Suppose we execute:
anExpression := expressionStack.top();
anExpression.simplify();
Since we are using aliasing, the object anExpression is actually still in the stack (we didn't remove it) but we have caused that very object to become simplified. If the assignment operator simply copied the representation of an object to a new location then the simplify would be performed on the data at the new location, and the object in the stack would not be modified. Instead, with aliases, we operate on a single object. Therefore we don't need to put the object back into the stack after performing simplify because it was never removed.
Objects can even send messages to themselves. Often a method for some class will want to execute another method in the same class. This is done by sending a message to itself. The syntax for it uses the parameter self together with a method name as in self.methodName(), with any required parameters. It is understood that the message is being sent to object executing the current method. Actually, there is nothing magic about the name self that we use as the first parameter in our methods. The only thing that is important is that its type is that of the class of the method.
In defining the class FiniteStack.T above, we did not show the details of the Object.T class on which it depends. The declaration of this class is contained in the interface Object.i3 shown below:
INTERFACE Object;
IMPORT Wr;
EXCEPTION fatal;
TYPE T = OBJECT
METHODS
writeIt(f:Wr.T) := WriteIt;
assert(a:BOOLEAN) RAISES {fatal} := Assert;
shallowClone():T = ShallowClone; (* DO NOT OVERRIDE *)
clone():T := Clone;
copyFields(o:T) := CopyFields;
equal(o:T):BOOLEAN := Equal;
END;
PROCEDURE Error(s:TEXT) RAISES {fatal};
PROCEDURE FailNil(o:REFANY) RAISES {fatal};
PROCEDURE WriteIt(self:T; f:Wr.T);
PROCEDURE Assert(self:T;a:BOOLEAN) RAISES {fatal};
PROCEDURE Equal(self:T; o:T):BOOLEAN ;
PROCEDURE ShallowClone(self:T):T ;
PROCEDURE Clone(self:T):T ;
PROCEDURE CopyFields(self:T; o:T) ;
PROCEDURE DoWrite(f:Wr.T; o:REFANY);
PROCEDURE AreEqual(m,n: REFANY):BOOLEAN;
END Object.
The associated implementation file Object.m3 is:
MODULE Object;
IMPORT Wr, Thread, Stdio, Text, RTAllocator (*, CopyBytes *) ;
PROCEDURE comment(t:TEXT) =
BEGIN
TRY
Wr.PutText(Stdio.stdout, t);
Wr.PutChar(Stdio.stdout, '\n');
Wr.Flush(Stdio.stdout);
EXCEPT
| Thread.Alerted =>
| Wr.Failure =>
END;
END comment;
PROCEDURE DoWrite( f:Wr.T; o:REFANY) =
BEGIN
IF f = NIL THEN f := Stdio.stdout; END;
TRY
IF o = NIL THEN
Wr.PutText(f, "NIL ");
ELSIF ISTYPE(o,T) THEN
NARROW(o,T).writeIt(f);
ELSIF ISTYPE(o,TEXT) THEN
Wr.PutText(f, NARROW(o, TEXT));
ELSE
Wr.PutText(f, "aValue ");
END;
EXCEPT
| Thread.Alerted =>
| Wr.Failure =>
END;
END DoWrite;
PROCEDURE AreEqual(m,n: REFANY):BOOLEAN =
BEGIN
IF m = NIL THEN
RETURN FALSE; (* or RETURN n = NIL ?? *)
ELSIF ISTYPE(m,T) THEN
RETURN NARROW(m,T).equal(n);
ELSIF ISTYPE(m,TEXT) THEN
IF ISTYPE(n,TEXT) THEN
RETURN Text.Equal(m,n);
ELSE
RETURN FALSE;
END;
ELSE
RETURN m = n;
END;
END AreEqual;
PROCEDURE Error(s:TEXT) RAISES {fatal} =
BEGIN
TRY
Wr.PutText(Stdio.stderr,s);
EXCEPT
| Thread.Alerted =>
| Wr.Failure =>
END;
RAISE fatal;
END Error;
PROCEDURE FailNil(o:REFANY) RAISES {fatal} =
BEGIN
IF o = NIL THEN Error( "A Reference is NIL."); END;
END FailNil;
PROCEDURE WriteIt(self:T; f:Wr.T) =
BEGIN
IF f = NIL THEN f := Stdio.stdout; END;
TRY
Wr.PutText(f," An Object ");
EXCEPT
| Thread.Alerted =>
| Wr.Failure =>
END;
END WriteIt;
PROCEDURE Assert(self:T;a:BOOLEAN) RAISES {fatal}=
BEGIN
IF NOT a THEN Error( "Assertion Failed."); END;
END Assert;
PROCEDURE Equal(self:T; o:T):BOOLEAN =
BEGIN
RETURN self = o;
END Equal;
PROCEDURE ShallowClone(self: T):T =
VAR result := self;
BEGIN
result := RTAllocator.NewTraced(TYPECODE (self));
(* CopyBytes.P(self,result,ADRSIZE(self)); *)
result.copyFields(self);
RETURN result;
END ShallowClone;
PROCEDURE Clone(self: T):T =
BEGIN
RETURN self.shallowClone();
END Clone;
PROCEDURE CopyFields(self:T; o:T) =
BEGIN
(* Nothing *)
(* Copy all fields of o into fields of self *)
END CopyFields; (* Override whenever you add new fields to an heir. *)
BEGIN
END Object.
These methods will be discussed shortly. Some of them are merely templates for expansion. All classes in this library are descendants of Object.T. There are two reasons for this. The first is that we may guarantee that all objects will then have some basic functionality, such as is provided by writeIt. More importantly, however, will be that we will be able to form lists and sets and trees, etc., using any of these objects as the contents. We will be able to construct lists of trees as easily as we can create lists of integers. This will be discussed again when we talk about collections.
The class Object.T was used in two different ways in FiniteStack.T. First as an ordinary type: some of the methods of FiniteStack.T had parameters or return values that can be of this type. This is because Object.T is a class type and hence a subtype of REFANY. Thus we can have a finite stack of elements of type Object.T. Second, and more importantly though, the FiniteStack.T class itself was defined to be a subclass of the Object.T class. This was done by the occurrence of Object.T as the parent class in the declaration of the public part of FiniteStack.T.
T <: Public;
Public = Object.T OBJECT
...
END;
We say that FiniteStack.T inherits from FiniteStack.Public, which in turn inherits from Object.T. Thus, we say that FiniteStack.Public (and indirectly, FiniteStack.T) is derived from Object.T, or is a subclass of Object.T. By that we mean that every object in FiniteStack.T is automatically a member of Object.T. It also means that every reference to an FiniteStack.T is compatible with a reference variable of type Object.T. Also, since Object.T is a subclass of ROOT, which is itself a subtype of REFANY, we know that every variable of type FiniteStack.T is actually a pointer variable.
Inheritance provides a mechanism which permits an object to belong to more than one class. Thus it provides a way for the sets represented by the classes to overlap. If FiniteStack.T inherits from Object.T, then all objects of class FiniteStack.T are objects of class Object.T, so that FiniteStack.T is contained in Object.T.
Inheritance
Using one class to define another by declaring only the new features. Defines a subclass relationship between the original (parent) class and the new class. All objects in the new class are members of the old class.
Notice that Object.T has no instance variables and it has a few methods, most of which don't do much. It is not intended that many variables will be given the type Object.T, or any objects created with the type, so Object.T is an example of what is called an abstract class. If it were not an abstract class we would have included a generator function Object.New() so that such objects would be easy to create.
Abstract Class An actual class which is the union of all of its subclasses. It has no objects which are not also objects of some subclass. In our library it may be recognized by the absence of a generator function. |
Concrete Class An actual class which may contain objects not in any subclass. May be recognized by the presence of a generator function. |
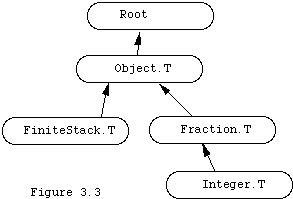
The class FiniteStack.T (which is concrete, as evidenced by its generator function) is called a subclass (sort of like subset) of Object.T, and things become objects in an abstract class like Object.T only by being created within some concrete subclass like FiniteStack.T. If we declare a new class to be a subclass of FiniteStack.T then objects in the new class will be instances of that class, as well as instances of FiniteStack.T and Object.T. Each class may declare itself to be a subclass of one other class (or no class at all, but for us only Object.T will declare no "ancestor") and so classes in Modula-3 form a hierarchical structure defined by inheritance. The structure is actually a tree with edges represented by arrows pointing at the ancestor classes. For example we shall define Fraction.T below as another subclass of Object.T and we could (but won't) define Integer.T as a subclass of Fraction.T. Fraction.T will treat fractions with numerators and denominators as objects. Integer.T would treat ordinary integers as objects. We would then have a hierarchy as shown in Figure 3.3.
Alternatively we could show subclasses in the same way that we ordinarily show subsets as in Figure 3.4.
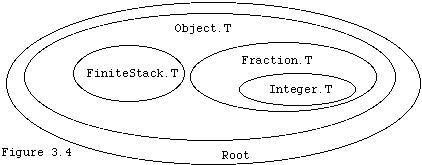
This last picture demonstrates the general idea that we think of objects in class Fraction.T as just special types of objects of type Object.T, and elements of Integer.T as just special instances of Fraction.T.
Since we can directly inherit from only one class, we say that Modula-3 is a single inheritance language. Similarly, Object Pascal and Smalltalk are also single inheritance languages, but C++ has multiple inheritance where a class may declare several immediate ancestors. With single inheritance the structure of the classes is hierarchical or treelike, with some class as the root of the tree or the ultimate ancestor of all classes. If multiple inheritance is possible the inheritance structure is a directed graph with no cycles rather than a tree.
Notice that inheritance is transitive, so that Integer.T being a subclass of Fraction.T, and Fraction.T a subclass of Object.T, it follows that Integer.T is a subclass of Object.T. For any given class, the ancestors form a chain back to ROOT. For any given class the descendants of that class form a tree spreading out from the class.
When one class (the sub-class) inherits (directly or indirectly) from another (the super-class), the objects of the class get methods and instance variables from the super-class and hence from all of its ancestors. Thus if Object.T declared an instance variable ident then all objects in class FiniteStack.T would have such an instance variable as well. Likewise, objects in FiniteStack.T do have a method, writeIt, and another, clone, etc. Therefore, we could have implemented push so that we first check that the stack is not full so that we can halt the computation if it is. We can accomplish this with the assert method defined in Object. To do this, the object executing the push method would have to send the assert message to itself. This can be accomplished from within any method of any class descendant from Object.T by using self as the target of the message.
self.assert(NOT self.full());
Then the same object, self, a FiniteStack.T object, would execute the assert method, and if the object is indeed full, printing an "assertion failed" message and then halting the execution of the program.
It is possible that an inherited method (one declared by some ancestor) provides inappropriate action in the current class. This is the case here with the writeIt method. If we were to say
expressionStack.writeIt(Stdio.stdout);
the stack would execute the method it inherited and we would see the string
An Object
appear in the output. When a method is inherited it is possible to redefine the action that it carries out when executed by an object of the new class. In this case we would redeclare writeIt as an override in the FiniteStack.T class definition, and redefine it in the implementation file of its definition as:
REVEAL
T = FiniteSTack.Public BRANDED OBJECT
...
OVERRIDES
writeIt := WriteIt;
...
END;
...
PROCEDURE WriteIt(self: T; f:Wr.T) =
BEGIN
FOR i := self.fTop TO 0 BY -1 DO
self.fElements [i].writeIt(f);
Wr.PutText(f," ");
END;
END WriteIt;
We now send the writeIt message to each object in the stack, writing the stack from top to bottom. Note that we process it from the top down, as this is more in keeping with the idea of what a stack is. This cannot be overemphasized. There is a key principle here:
Principle of Abstraction
The processing provided by a class should always be in accord with the nature of the abstraction on which the class is based.
Inheritance is very powerful if we combine the above ideas with the ideas of indirect or reference variables. Suppose that we have declared and defined the Fraction.T and Integer.T classes discussed above. We shall see below that Fraction.T will declare a method named add. Assume that Integer.T has a method isPrime, which returns a BOOLEAN TRUE if the integer is a prime number.
Updated (but simplified)class photos are shown in Figure 3.5 , with inheritance indicated by arrows between the classes. Note that as we descend the hierarchy, we don't lose the public methods of the ancestors, but we may add additional ones. The deeper we get in the inheritance structure, the more sophisticated our classes, and hence the objects, become.
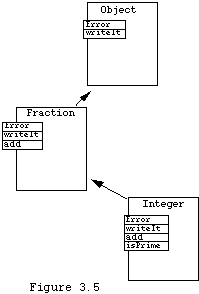
Then suppose that we have declared two reference variables myFraction and myInteger as in
myFraction: Fraction.T;
myInteger: Integer.T;
The properties of reference variables, the nature of object identity, and the fact that subclasses are like subsets, together imply that it is possible to make the assignment
myFraction := myInteger;
and that myFraction, even though declared to be a name associated with class Fraction.T, is now a reference to an Integer.T. This is indeed the case. Note that we are assuming this integer object was properly created in the first place, with a call to Integer.New.
This integer object, masquerading under the name myFraction, ought to behave just like any other integer. Therefore, if writeIt was overridden in Fraction.T and then again overridden in Integer.T, and if we next say
myFraction.writeIt(Stdio.stdout);
then the method executed is the version known to the object itself, which is an Integer.T, not the version from class Fraction.T. Thus, in a very real sense the object is seen to be autonomous. We can't get it to behave improperly even if we reference it with a name associated with an ancestor class. See Exercises 11 and 12 <<<<MAY CHANGE>>> at the end of this chapter.
Virtual method A method of a class that, when used with a reference variable, is interpreted in the most specific way possible. The method executed is the method associated with the object itself, not necessarily the name associated with the class of the variable used to refer to the object. In Modula-3, all methods are virtual. |
When referred to by a reference variable, the above Integer.T object should be able to respond to the message ...isPrime, but here we have a difficulty. Modula-3 is very strongly typed, , and it is typed by the compiler, which means that the names are typed. Thus if we try to say myFraction.isPrime(), we will get a complaint from the compiler that myFraction is a reference to type Fraction.T and there is no such method in that class. The compiler actually has no way to know that we have made an assignment "up the hierarchy" and that myFraction will reference an Integer.T at this spot at run time. If the programmer can verify that in every execution of the program myFraction will always reference an Integer.T at this spot then we can get the object to respond to isPrime by Narrowing the name as in:
NARROW(myFraction, Integer.T).isPrime();
Note that the type name is used as a parameter to the function NARROW, which returns a reference to an object of that type. One way to think of narrowing, sometimes called type casting, is that it simply reassures the compiler that the programmer knows what is best and can verify externally that myFraction always represents an Integer.T here. Actually it does more, as will be discussed shortly. Note that if you use narrowing (we will, in important ways) and you are wrong, and myFraction holds a reference to something not in Integer.T then at run time you will get an error. It is an error that will be caught by the run time system and your program will be halted. Narrowing must be used carefully, and only when one can prove that it is valid. Narrowing can never make a correct program incorrect, nor an incorrect program correct. It must be used only when the programmer is willing and able to take on the burden of correctness.
FiniteStack.T is used to hold, in a structured (LIFO) way, references to objects of other classes. Therefore it is an example of a collection class. Often we shall want to push objects from several classes onto a single stack. This is why the element type for the elements array was declared to be a REFANY, which means any reference, including any object reference. When we pop the objects off the stack we get things whose class is not known to the compiler, other than as REFANY. We shall need to narrow them so that the compiler will let us operate on them after they are removed.
This ability to use a single name, such as myFraction, to reference different kinds of things is a special kind of strong typing. Standard "strong typing" (such as found in Pascal) is very strict about every name, with everything having only a single type. The same is actually true here with the difference being that in Modula-3 the types are not disjoint. A class type consists of all objects in a class and in all subclasses of that class. Assignment compatibility is consistent with this view. If a name is declared to be associated with a class type, then it can refer to any object in that class or in any subclass of that class. We say that Modula-3 introduces type polymorphism into the language, as we may associate "many forms" or types with a name.
Type Polymorphism The ability of a variable to refer to objects of many different types. |
It is important to note that both variables and objects have types. The type of a variable is decided by the programmer who gives a declaration. The compiler sees this declaration and associates a type with the variable name. From then on, that name may be associated only with that type (or a subtype). Importantly, typing of variable names is at compile time. On the other hand, objects are given a type when they are created using the built-in function NEW. The parameter used with NEW is a type that is assigned to the newly created object. From then on, the object may be referred to by many different names (aliases), but its type never changes. An object always has a single type. The names that refer to it are names associated with its own type (creation type) or the types of superclasses of that type. Importantly, typing of objects is at run time.
Continuing the discussion of Object.T, some of its methods are specifically included for no other purpose than to be overridden. The method writeIt is such a method. Normally every class should override writeIt, and so (as we never directly create objects of type Object.T) we should never execute the method. It is here to provide a protocol which other inheriting classes will use in a consistent way. If every class declared a method to show an external representation of the object, but all used different names, it would be difficult to remember what name was used in what class. We are thus programming here according to the Rule of Seven discussed earlier. Some methods, especially here in the root class, are intended never to be overridden. Examples are shallowClone and assert. Others, such as copyFields are intended to be overridden in every class. The method Clone is provided so that we may override it as necessary to create objects identical to the one that executes the method.
The file Object.m3 also declares two public procedures that are not methods: FailNil and Error. FailNil is here because a call to NEW may fail. It is used within generator functions as:
result := NEW(T);
Object.FailNil(result);
. . .
and causes a structured shutdown of the program rather than a crash if the heap is out of room. Note that it can't be a method, as it is called in situations in which there may be no object to execute it. We similarly provide the ordinary function Error, which writes out its string parameter and the program is halted. It allows the programmer to shutdown a program when the program detects an error from which it cannot recover.
Finally, in this section we look at just what is inherited, and what is not. In terms of the definition of Modula-3 what is inherited is the physical structure of the instance variables, the method declarations, and for those methods not overridden, the code of the inherited methods. It is not possible to drop an instance variable or a method name in a subclass, nor is it possible to change the type of an instance variable, or any parameter of an inherited method. We can add new stuff, or we can redefine the code for a method. That is all.
The above description is very physical, and could be misleading to the user attempting to develop a good style of object oriented programming. Conceptually we want to think that we are inheriting much more than just code and bits. Specifically, when we define an FiniteStack.T class, we declare that it exhibits a LIFO protocol, and we are careful to specify how that is interpreted in terms of the actions of push and pop. If we create a subclass of FiniteStack.T the subclass is supposed to be "like a subset" of FiniteStack.T, or in other words, a specialization of FiniteStack.T. This means in particular that subclasses of FiniteStack.T should still be LIFO, and as the name is FiniteStack.T, they should also be finite. Another way to say this is to say that the relationship between a subclass and its superclass is ISA, pronounced "is a". Thus, in the above, an Integer.T ISA Fraction.T, and a mathematician would agree. Nothing in the Modula-3 language definition or implementation enforces this however. It is necessary for the programmer, then, to be aware of what he or she is doing when using inheritance, and generally speaking to ensure that a subclass is really a specialization of its superclass.
ISA A relationship between a subclass and its superclass. Other relationships are possible but this is the norm. An object of a subclass ISA (is a) object of its superclass. It exhibits all of the properties of a superclass object. Implies that the subclass is a specialization of the superclass. |
Occasionally it is useful and even necessary to program as if "ISA" weren't the norm. In these cases it is important to be clear in the documentation of a class that it is only "LIKE" its superclass. Sometimes we need to create some software in a hurry, and we look at the stuff we already have, and find that some class does most of what we want. We may need to look at the code to determine this, although the specifications should be adequate. Then, to create the new stuff, it is tempting and useful to subclass the existing class, ignoring the intent and the specification of the original, but only taking advantage of the code. Then the subclass objects are only "similar" to the superclass objects, and we say that the relationship between the subclass and superclass is ISLIKE, rather than ISA. For example it is possible to implement a queue (first in-first out, FIFO structure) by subclassing a stack, but queues aren't specialized stacks, but only similar to stacks. The programmer needs to be careful that she/he recognizes when each technique is being used, with ISA being more important. The reason for this comes back to the Rule of Seven. The more similarities there are, the less has to be remembered. If our class hierarchy is a specialization hierarchy, with each class adding behavior, but not changing it, then we achieve a conceptual unity that will help us use what we have and avoid the errors that come from misunderstanding what we do.
ISLike A relationship between a class and its superclass. A weaker relationship than ISA. It is used only for code reuse rather than as an abstraction mechanism. Implies that the subclass is a modification of its superclass. Some item of the semantics has changed. |
The class FiniteStack.T discussed above is actually an example of a general type of class called a collection. The idea of a collection is that it is a container of some sort for objects (or data). Examples of collections are sets, lists, stacks, arrays, dictionaries, and several others. In fact, what we shall be collecting in our collections are references to values, usually objects. Since we may have several references to the same object, the same object can be a member of several collections simultaneously. An object can also be processed by some function while it is a member, so that we don't need to remove elements from sets or lists to manipulate them. An implication of this is that removal of an object from a collection never implies its destruction; it may still be referenced from other places in the program. Since the collections store references to objects rather than copies of objects we don't have to worry about updating all copies of some information when one copy changes. Since we permit several aliases, the owner of a piece of information need not give up access to an object when inserting it into a list or stack.
Since a collection is a general idea, it can be specialized. And since classes are a way to implement specialization it will be useful for us to create a class Collection.T. Most of the classes that we discuss in this book are either subclasses of Collection.T or of another major grouping, Magnitude.T, which is discussed in the next section. Since collections "store" objects we shall need ways to get objects into a collection, ways to get them out, and ways to find out what information is in the collection. Different subclasses will use different methods, with different names, for their primary insertion and deletion operations. For stacks the operations are traditionally called push and pop, for queues they are called enqueue and dequeue. But all collections exhibit an "inserting" and a "removing" behavior. Therefore the class Collection.T will need a method insert, and a method remove, which will be inherited by all subclasses, and will be overridden by most of them.
The "things" to be inserted into our collections will always be of type REFANY, or references to values. Most of the uses of collections in this book will use objects descended from Object.T. This has benefits and a cost. The benefit is that we may have lists or stacks of anything that we build here, since they will all derive from Object.T. We may even have stacks of lists or lists of stacks. We can even have heterogeneous collections such as a stack that simultaneously contains fractions and lists. We don't need to commit to some particular type, since the types are extendible by inheritance. The cost is that if we wish to collect something that is not a REFANY we will have to build a special structure to serve as a "package" of the thing that we really want. One easy way to do this is to create a class, derived from Object.T, that has the value as an instance variable.
INTERFACE Collection;
IMPORT Object, Wr;
TYPE (* Three Abstract Classes *)
ActionProc = PROCEDURE(o: REFANY);
TransformProc = PROCEDURE(o: REFANY):REFANY;
PredicateProc = PROCEDURE(o: REFANY):BOOLEAN;
T = Object.T OBJECT (* Collection of REFANY objects *)
METHODS
insert(o:REFANY) ; (* := NIL *)
remove(o:REFANY) ; (* := NIL *)
newIterator():Iterator ;(* := NIL *)
eachDo(DoIt:ActionProc) ;(* := NIL *)
firstThat(checkIt:PredicateProc):REFANY := FirstThat;
select(c:T; checkIt:PredicateProc) := Select;
reject(c:T; checkIt:PredicateProc) := Reject;
collect(c:T; transformIt:TransformProc) := Collect;
empty():BOOLEAN := Empty;
element(o:REFANY):BOOLEAN := Element;
cardinality():INTEGER := Cardinality;
OVERRIDES
writeIt := WriteIt;
END;
PROCEDURE FirstThat(self:T; checkIt:PredicateProc):REFANY ;
PROCEDURE Select(self:T; c:T; checkIt:PredicateProc) ;
PROCEDURE Reject(self:T; c:T; checkIt:PredicateProc) ;
PROCEDURE Collect(self:T; c:T; transformIt:TransformProc) ;
PROCEDURE Empty(self:T):BOOLEAN ;
PROCEDURE Element(self:T; o:REFANY):BOOLEAN ;
PROCEDURE Cardinality(self:T):INTEGER ;
PROCEDURE WriteIt(self:T; f:Wr.T) ;
TYPE
Iterator <: PublicIterator;
PublicIterator = Object.T OBJECT
METHODS
initIterator(c: T): Iterator;
nextItem(VAR o: REFANY):BOOLEAN ; (* := NIL *)
reset() ; (* := NIL *)
short();
done():BOOLEAN;
END;
Position <: PublicPosition;
PublicPosition = Object.T OBJECT
METHODS
initPosition(c: T):Position;
reset() ; (* := NIL *)
END;
END Collection.
Note that the insert and remove methods were marked in comments as ":= NIL." This is the way we indicate a function that has no body and which is intended entirely to be overridden in subclasses. The presence of such functions indicates that Collection.T is abstract. Modula-3 in fact, will not let us create such objects directly, we can only create objects of subclasses in which all of the unimplemented methods have been redefined. The reader will also note that there is no NewCollection generator function. There will be no objects in this class that are not also in some subclass. That doesn't mean that the class is useless. It serves two important purposes. First, it defines a protocol of method/message names that will be preserved by all subclasses. For example if we were to improve our FiniteStack.T class from the above, we would want to make it a subclass of Collection.T. Then we would want insert to be implemented within FiniteStack.T as a call to push. That way we would get the advantage of the generality of an insert method, while strictly maintaining the LIFO protocol of a stack.
The second purpose served by the class is that we can include here some very useful code, which will be inherited and probably not overridden, and which all subclasses will find useful. We shall show how writeIt can be written here to guarantee that any collection will write out all of its elements. The method empty is an example of this, being implemented in terms of cardinality. Before we can describe the implementation we need to discuss another fundamental idea.
Collections being containers of many things, it is often necessary to process all of the elements of a collection in some way. For example to count or write the objects in a collection we need to access them as a whole, without disturbing the contents of the collection. The thing that makes this possible is the idea of an iterator.
Iterator A mechanism for sequentially processing the elements of any collection. Iterators generalize the operation of FOR loops on array structures. |
Iterators are the means of processing the elements of a collection one at a time until all have been used. Usually this means sending some message like writeIt to each element in the collection, or possibly sending each object of a collection as a parameter to some processing procedure. This idea is embodied in the abstract class Collection.Iterator. Each subclass of Collection.T (Lists.T for example) will have an associated iterator class (in this case Lists.Iterator), which is a subclass of Collection.Iterator. The declaration of the iterator protocol follows, extracted from the Collection interface above is:
TYPE
Iterator <: PublicIterator;
PublicIterator = Object.T OBJECT
METHODS
initIterator(c: T): Iterator;
nextItem(VAR o: REFANY):BOOLEAN ; (* := NIL *)
(* If all items have been yielded then return FALSE. Otherwise return TRUE
and set o to the next unyielded item of self. *)
reset() ; (* := NIL *)
(* Reset to the beginning as if no elements had yet been yielded. *)
short();
(* Short-circuit the iterator so that nextItem will next return FALSE. *)
done():BOOLEAN;
(* TRUE if all items have been yielded (or none were initially present). *)
END;
INTERFACE PRCollection;
IMPORT Object;
FROM Collection IMPORT T, Iterator,Position,PublicIterator,PublicPosition;
REVEAL
Iterator = PublicIterator BRANDED OBJECT
fCollection : T;
fDone : BOOLEAN;
OVERRIDES
initIterator := InitIterator;
short := Short;
done := Done;
writeIt := WriteIter;
copyFields := CopyIterFields;
END;
PROCEDURE InitIterator(self: Iterator; c: T): Iterator ;
PROCEDURE Short(self: Iterator; ) ;
PROCEDURE Done(self: Iterator):BOOLEAN ;
PROCEDURE WriteIter(self: Iterator; f, Wr.T) ;
PROCEDURE CopyIterFields(self: Iterator; o:Object.T) ;
REVEAL
Position = PublicPosition BRANDED OBJECT
fCollection: T;
OVERRIDES
initPosition := InitPosition;
writeIt := WritePos;
copyFields := CopyPositionFields;
END;
PROCEDURE InitPosition(self: Position; c:T):Position ;
PROCEDURE WritePos(self: Position; f: Wr.T) ;
PROCEDURE CopyPositionFields(self: Position; o:Object.T) ;
END PRCollection.
Here we have used a different form of IMPORT that permits us to avoid using qualified names for the items specifically imported from Collection. Among other things, the revelation for the Iterator class shows that every iterator object has an fCollection instance variable, which holds a reference to the collection on which the iterator operates. The fDone variable is set to true for an empty collection, and also when the iterator is finished with its work of iterating, or "yielding" each of the elements of its collection.
Within any collection class is a method newIterator, which creates and initializes an iterator of the appropriate kind for that class. This is the only appropriate way to create an iterator. The initIterator method needs to be executed for any iterator, and it is simply:
PROCEDURE InitIterator(self: Iterator; c: T): Iterator =
BEGIN
self.fCollection := c;
self.fDone := c.empty();
RETURN self;
END InitIterator;
Subclasses of Collection.T that provide more specialized iterators will also provide more specialized initializations, but those methods will always call this one. An iterator will always produce the objects in a given collection. This is the collection mentioned in its initialization, and saved in its instance variable. Remember that only a reference is saved. The collection is not copied by this code. The instance variable fDone remembers whether there are any more elements to yield. If the collection is empty the value will be true. Note that an iterator may not operate correctly if a collection is changed after an iterator is initialized (or reset). This means that it is not safe in general to use an iterator as a mechanism for modifying the collection over which it iterates. See Chapter 10 for some ideas about how this requirement may be relaxed. Reset will permit an iterator to be reused.
The objects in the collection are actually accessed by calling an iterator's nextItem method. It is used in the following way in virtually all cases. Suppose that we have a Lists.T subclass of Collection.T (Lists.T is described briefly in chapter 4 and completely in chapter 6), and a Lists.Iterator subclass of Collection.Iterator. Suppose that aList has type Lists.T and it has been created, initialized, and used, so that it contains some objects. Suppose that IT is declared to be of class Collection.Iterator, but that it has only been declared, not created. Suppose that we also have a reference variable aValue declared to be of type REFANY. Then to write all objects in aList we could write:
IT := aList.newIterator(); (* creates a list iterator*)
WHILE IT.nextItem(aValue) DO
Object.DoWrite(Stdio.stdout, aValue);
END;
The repeated sending of the nextItem message will yield successive elements of the list aList, and the function return value will be true as long as there is more to yield. This is very much like the way that a for loop is used to iterate over an array (actually over the subscripts of the array, which form a primitive type of collection). This is a situation in which narrowing comes to our aid. Note that variable aValue has type REFANY, the parameter of nextItem. However, we actually store values with much more specific types than REFANY. If we had been storing only objects in some class Expression.T in the list, and if such objects respond to the simplify message then we could simplify all of them in the list with
IT := aList.newIterator(); (* creates a list iterator *)
WHILE IT.nextItem(aValue) DO
NARROW((aValue, Expression.T).simplify();
The narrowing is needed as aValue has a declared type of REFANY, which does not have a simplify method (or any method). Note that it doesn't help to declare aValue as type Expression.T, because then it conflicts with the parameter type of nextItem.
The nextItem method of Collection.Iterator uses a VAR parameter to pass information back from the routine nextItem to its caller. In this way, nextItem gives us access to a new item from a collection each time it is called. The reason that we do not return this item as the function result is that we want to use that for loop control, returning FALSE only when nothing could be returned for the reference parameter.
Note that in the definition of Collection.Iterator we have an instance variable fCollection which has a class type. We can say that an iterator HASA collection. This is yet another relationship between classes. An object in one class HASA object in another if one of its instance variables is in that other class.
HASA A relationship between classes. The relationship A HASA B is true if B is used to implement A. One of A's components is an element in B. Sometimes we make a choice between ISA and HASA when designing a new class. |
Since the class Collection.T is abstract and there will be no objects immediately in this class it has no instance variables to implement a collection. The subclasses will create these. Therefore the insert and remove methods cannot be implemented here
insert(o:REFANY) ; (* := NIL *)
(* Insert o into self. *)
remove(o:REFANY) ; (* := NIL *)
(* Remove o from self if present. *)
Well, so far we have described how useless Collection.T and Collection.Iterator are and how they can be made useful by creating subclasses. Actually we can show how to implement the method writeIt here, even though we don't know how an actual collection, like a list, stack, or binary tree will be implemented.
PROCEDURE WriteIt(self:T; f: Wr.T) =
VAR It : Iterator;
o: REFANY;
BEGIN
It := self.newIterator();
WHILE It.nextItem(o) DO
Object.DoWrite(f, o);
Wr.PutText(f," ");
END;
END WriteIt;
This writes a space separated list of the objects in any collection. Note that all objects inherit or override writeIt, as this method was first declared in Object.T. There is a very subtle but extremely important point to be made about this code. Suppose that writeIt is not overridden in some subclass, say Lists.T, of Collection.T. Then suppose a client sends the writeIt message to aList in class Lists.T. Then aList will be the one executing the method above, and aList will be the one sending itself the newIterator message which appears there. Note that Lists.T will override newIterator (it is a MUST OVERRIDE method). Therefore, aList when executing newIterator will execute its own version, not the version (unimplemented version) in Collection.T. This is in spite of the fact that the code above which is executed IS from class Collection.T. This is an instance of the dynamic binding principle at work, and it is one of the important things that makes Object Oriented Programming special:
Dynamic Binding Principle
Every message that is sent is interpreted in the context of the object executing the method.
Because of this principle we can create a method in a superclass and mention other methods which will be called at run time even though they haven't been created yet. All that is required is that we establish in this class (or a superclass) the protocol for the method to be called. That is, its name, and its parameter list. If an object in some subclass executes this method, it will interpret all messages in the method in light of its own definition, taking into account any overrides of the methods known to the class that actually contains the method executing. Strange perhaps, when you first think about it, but very useful. Also the dynamic binding principle on which it is based is very simple and easy to remember. It is also central to the fundamental idea of object oriented programming, that the objects should be autonomous and in control
We mention the method, copyFields, that was originally declared in Object.T and will be redefined in every class. The dynamic binding principle assures us that if we send some object a copyFields message then that object will respond by copying its own fields, even if that object is currently being referred to by a name associated with a superclass of the actual object. In turn, this will assure us that ShallowClone works properly, and thus that Clone does also. We say that this makes copyFields polymorphic, as it works on many types.
The class Magnitude.T embodies our ideas of size and quantity. It has many subclasses, like Fraction.T, Complex.T, and even Integers.T, which treats ordinary integers as if they were objects. The key to magnitudes is the comparison of objects with methods like less and equal. The abstraction on which magnitudes are built is the idea of the partial ordering of a set. A set is in partial order if there is a relation <= between elements of the set which satisfies the following rules
Partial Order a) reflexive (a <= a for any a), b) transitive (a <= b and b <= c implies a <= c), and c) anti-symmetric ( a <= b and b <= a implies a = b). |
A partial order is called total, if in addition to the above, we have
d) for any pair of elements a, b, either a <= b or b <= a.
The integers are in total order with the usual <=. A hierarchical structure, like our class structure (if we consider only inheritance from Object.T) represents a partial order (but not a total order) if we let <= stand for the ancestor-descendant relationship. That is we say class A <= class B if B is an ancestor of A or is the same class.
The class protocol for Magnitude.T is as follows:
INTERFACE Magnitude;
IMPORT Object, Wr;
TYPE
T = Object.T OBJECT
METHODS
less(m:T):BOOLEAN ;
hash():CARDINAL;
notEqual(m:T):BOOLEAN := NotEqual;
greater(m:T):BOOLEAN := Greater;
lessEqual(m:T):BOOLEAN := LessEqual;
greaterEqual(m:T):BOOLEAN := GreaterEqual;
between(first:T; second:T):BOOLEAN := Between;
min(m:T):T := Min;
max(m:T):T := Max;
OVERRIDES
writeIt := WriteIt;
equal := Equal;
END;
PROCEDURE NotEqual(self: T; m:T):BOOLEAN ;
PROCEDURE Greater(self: T; m:T):BOOLEAN ;
PROCEDURE LessEqual(self: T; m:T):BOOLEAN ;
PROCEDURE GreaterEqual(self: T; m:T):BOOLEAN ;
PROCEDURE Between(self: T; first:T; second:T):BOOLEAN ;
PROCEDURE Min(self: T; m:T):T ;
PROCEDURE Max(self: T; m:T):T ;
PROCEDURE WriteIt(self:T; f: Wr.T) ;
PROCEDURE Equal(self: T; o:Object.T):BOOLEAN ;
END Magnitude.
Note that Object.T implemented an equal method. In that class objects are equal only if they are the same object (aliases). In magnitudes, we have a fundamentally different idea. Magnitudes are equal if they have the same "size", by the anti-symmetric law. For this reason, equal is reimplemented here as an error call.
PROCEDURE Equal(self: T; o:Object.T):BOOLEAN =
BEGIN
Object.Error("Magnitude Equal: Subclass must implement.");
END Equal;
The method greater can be implemented in terms of the required less and so it is done as an aid to subclasses.
PROCEDURE Greater(self: T; m:T):BOOLEAN =
BEGIN
RETURN m.less(self);
END Greater;
The others are similar. For example:
PROCEDURE Between(self: T; first:T; second:T):BOOLEAN =
BEGIN
RETURN self.greaterEqual(first) AND self.lessEqual(second);
END Between;
The typical use of these methods is in if and while statements as in
IF anExpression.less(aLeftHandSide) THEN
...
END;
Importantly, note that objects are compared with less and with lessEqual, not with < or <=, which work only on a restricted subset of Modula-3's built in data. These functional methods extend the idea of comparison to a large class of objects. We can compare not only integers, characters, etc., but also fractions, geometric figures, and whatever else we choose to make a subclass of Magnitude.T.
In this section we will give an implementation of the magnitude subclass Fraction.T. Fractions are magnitudes as they can be compared. Actually they are more. They are a member of an important set of subclasses of Magnitude.T called Numeric classes, as they can also be operated on with the usual arithmetic operators. We could implement the following numeric class, but we won't. If we did then Fraction.T would be a subclass of Numeric.
TYPE Numeric = Magnitude.T OBJECT
METHODS
add (b: Numeric);
(* Return the "sum" of self and b. Meaning depends on class of self. *)
subtract(b: Numeric);
multiply(b: Numeric);
divide(b: Numeric);
END;
This class won't really exist except in our documentation as its use as an abstract class requires that too many variable narrowings would need to be given in the concrete subclasses of it. Since it doesn't exist we call it a Pseudo Class. Since it is a pseudo class, Fraction.T actually subclasses Magnitude.T
Pseudo Class A purely conceptual class used to convey details of a protocol. Not actually declared or implemented. Recognized by its complete absence, except in documentation. |
The public interface for fractions is given below. Once again we see that only the new public methods are given here as well as a generator function.
INTERFACE Fraction;
IMPORT Object, Magnitude;
TYPE
T <: Public;
Public = Magnitude.T OBJECT
(* INVARIANT: Denominator is always positive.
Fraction is always lowest terms. *)
METHODS
add(f: T):T;
subtract(f: T):T;
multiply(f: T):T;
divide(f: T):T;
END;
PROCEDURE New(n,d: INTEGER):T; (* Return 0 if d=0 *)
END Fraction.
Since we wish to examine the implementation of this class we must first examine the private details from the interface PRFraction.i3.
INTERFACE PRFraction;
IMPORT Fraction, Magnitude, Object;
REVEAL
Fraction.T = Fraction.Public BRANDED OBJECT
fNumerator, fDenominator: INTEGER;
METHODS
initFraction(n,d: INTEGER): Fraction.T := InitFraction;
OVERRIDES
less := Less;
equal := Equal;
hash := Hash;
add := Add;
subtract := Subtract;
multiply := Multiply;
divide := Divide;
writeIt := WriteFraction;
copyFields := CopyFractionFields;
END;
PROCEDURE InitFraction(self: Fraction.T; n,d: INTEGER): Fraction.T ;
PROCEDURE Less(self: Fraction.T; m: Magnitude.T):BOOLEAN ;
PROCEDURE Equal(self: Fraction.T; o:Object.T):BOOLEAN ;
PROCEDURE Hash(self: Fraction.T):CARDINAL;
PROCEDURE Add(self: Fraction.T; f: Fraction.T):Fraction.T;
PROCEDURE Subtract(self: Fraction.T; f: Fraction.T):Fraction.T;
PROCEDURE Multiply(self: Fraction.T; f: Fraction.T):Fraction.T;
PROCEDURE Divide(self: Fraction.T; f: Fraction.T):Fraction.T;
PROCEDURE WriteFraction(self: Fraction.T; Wr.T) ;
PROCEDURE CopyFractionFields(self: Fraction.T; o: Object.T) ;
END PRFraction.
Note that we include the required overrides for Magnitude.T, and a consistent reworking (but not inheriting) of Numeric. Modula-3's strong typing won't let us redefine less as:
less(m: Fraction.T);
We have also included a class invariant as part of the documentation of the class. An invariant is a statement which can be guaranteed to be always true. In this case it means that to an external observer (client or subclass), we always have the numerator and denominator in lowest terms: any common factors will have been divided out of both. There will be short periods of time, while methods of this class execute that the invariant will not be true, but all methods will restore the truth of the statement before they exit, or else they must fail.
Class Invariant
A statement guaranteed by the implementor to be always true when observed from outside the class.
The implementation of this class depends on the following three support procedures, which are defined entirely within the implementation file Fraction.m3.
PROCEDURE Sgn (a: INTEGER): INTEGER =
BEGIN
IF a > 0 THEN RETURN 1;
ELSIF a = 0 THEN RETURN 0;
ELSE (* a < 0 *) RETURN -1;
END;
END Sgn;
PROCEDURE GCD(a,b: INTEGER): INTEGER =
(* Precondition: b > 0, a >= 0
Postcondition: Returns the gcd of a and b *)
VAR r: INTEGER;
BEGIN
IF a # 0 THEN
REPEAT
IF a < b THEN r := a; a := b; b := r; END;
a := a MOD b
UNTIL a <= 0;
END;
RETURN b
END GCD;
PROCEDURE Reduce (f: T) =
(* Precondition: denominator # 0
Postcondition: f is in lowest terms *)
VAR r: INTEGER;
BEGIN
r := GCD(ABS(f.fNumerator), ABS(f.fDenominator));
f.fNumerator := f.fNumerator DIV r;
f.fDenominator := f.fDenominator DIV r;
IF f.fDenominator < 0 THEN
f.fNumerator := - f.fNumerator;
f.fDenominator := - f.fDenominator;
END;
END Reduce;
Gcd and Reduce both list preconditions, which any user (in this case just routines in this implementation part) must guarantee before calling the procedure, and postconditions, which the code itself will guarantee, if the precondition is true on entry. This listing of pre and postconditions is entirely within the spirit of programming by implementing abstractions, and forms a guide to the programming.
Precondition
A fact that the user of a method or procedure must guarantee before calling the method or function. This is the user's responsibility.
Postcondition
A fact that the implementor will guarantee will be true after the routine finishes if all of its preconditions were true at the time of call.
Reduce is a very special function for this module. Notice that it makes reference to the actual fields of its parameter f. Normally we like to avoid this. This must be done sparingly to avoid serious problems in our software library. Every reference to the implementation variables of an object means another procedure (such as Reduce) that must be rebuilt whenever the implementation of the class whose variables it uses must change. We strive for a high degree of independence between the pieces of our library and this usage can get in the way of this.
Initialization is the key method in this class. Note that it implements the class invariant and respects the precondition of reduce which it calls.
PROCEDURE InitFraction(self: T; n,d: INTEGER): T =
BEGIN
IF d #0 THEN
self.fNumerator := n;
self.fDenominator := d;
Reduce(self);
ELSE
self.fNumerator := 0;
self.fDenominator := 1;
END;
RETURN self;
END InitFraction;
PROCEDURE New(n,d: INTEGER): T =
VAR result: T;
BEGIN
result := NEW(T);
Object.FailNil(result);
EVAL result.initFraction(n,d)
RETURN result;
END New;
The other methods are similar to add, using initialization to do the hard work:
PROCEDURE Add(self: T; f: T):T =
VAR result: T;
BEGIN
result := New(self.fNumerator * f.fDenominator +
self.fDenominator * f.fNumerator,
self.fDenominator * f.fDenominator);
Reduce(result);
RETURN result;
END Add;
PROCEDURE WriteFraction(self: T; f: Wr.T) =
BEGIN
Wr.PutChar(f, '<');
Wr.PutText(f, Fmt.Int(self.fNumerator));
Wr.PutChar(f, ',');
Wr.PutText(f, Fmt.Int(self.fDenominator));
Wr.PutChar(f, '>');
END WriteFraction;
Note that methods like add, as shown above are likely to overflow because of the extensive arithmetic done. This is true even when the result, reduced to lowest terms, is easily represented. One may use more sophisticated methods to help avoid this. A good (but not perfect) version of equal is shown below.
PROCEDURE Equal(self: T; o:Object.T):BOOLEAN =
VAR r, n, p: INTEGER;
BEGIN
IF ISTYPE(o, T) THEN WITH m = NARROW(o,T) DO
r := GCD(m.fDenominator, self.fDenominator);
p := self.fDenominator DIV r;
n := m.fDenominator DIV r;
RETURN self.fNumerator * n = p * m.fNumerator;
END; (* with *)
ELSE
RETURN FALSE;
END;
END Equal;
Since Fraction.T has new instance variables, we must also override copyFields. The standard template for this method first copies all inherited fields using the inherited copyFields method and then individually copies the new fields from the parameter object (which must be narrowed) to itself. The only purpose of this is to make shallowClone work properly.
PROCEDURE CopyFractionFields(self: T; o: Object.T) =
BEGIN
IF ISTYPE (o,T) THEN WITH temp = NARROW(o, T) DO
Magnitude.T.copyFields(self, temp);
(* Copy all new fields of temp into fields of self *)
self.fNumerator := temp.fNumerator;
self.fDenominator := temp.fDenominator;
END;
ELSE
Object.Error ("Copy Fraction Error");
END;
END CopyFractionFields; (* Override whenever you add new fields to an heir. *)
Note how we call the inherited copyfields method from within the new one: Magnitude.T.copyfields(self,temp). The call is not as a method at all, but as an ordinary procedure. This "direct" call guarantees that a specific procedure is called, rather than a polymorphic one. Once we have finished this class definition, we can do simple arithmetic on fractions. In fact, if we had a calculator program that correctly worked on integers it would be a matter of a few minutes work to turn it into a fraction calculator. This is because integers as objects (the class is Integers.T) have nearly the same protocol as this class. The calculator program would work by creating and manipulating integers through the Integers.T protocol. We need only change a few type declarations, and call the fraction generation function instead of the integer generator as appropriate to make the transformation. This is the power of programming with abstraction.
Classes may be concrete or abstract. An abstract class has some methods unimplemented. A class that is not abstract is a concrete class. Abstract classes are intended to form the common parent of other classes that need to have the same interface.
Classes describe their objects. They describe the features of each object within the class, which may be thought of as a set of its objects. The class features are instance variables and methods.
All methods obey the fundamental Dynamic Binding Principle, which guarantees that objects are permitted to act autonomously. Each object will determine precisely how it will interpret any message sent to it. It will determine this in accordance with its own personal type (class): the class it was given when it was created by the NEW operator.
This text describes a specific class structure, designed to illustrate data abstraction techniques and object oriented style of programming. The class structure emphasizes flexibility whenever possible.
The class Object.T describes basic functionality of all objects considered in this text. This functionality consists of a mechanism for determining the actual type of an object at run time, a facility for cloning an object and a means of writing a representation of the object on standard output.
The principle of inheritance implies that all objects in this system will be able to use and extend this basic functionality.
The class Collection.T, which inherits from Object.T, is the root of a large sub-hierarchy of classes, all of which provide a data collection service to their clients. Subclasses of Collection.T will handle lists, stacks, queues, and other specialized storage mechanisms. Collection.T provides insert and remove as well as an associated iteration mechanism.
Magnitude.T provides a means of creating classes with a partial order relationship between objects, by creating a comparison interface (less, greater, ...). We will create magnitude classes such as String.T.
Exercises
1. (3.2) Build and test the finite stack unit discussed in section 3.2. To test it you may push and pop any objects from any classes derived from Object.T. Characters are a good choice. To use characters, you must import the interface Character.i3 into your main program file. Character objects may be generated with the generator funciton asCharacter(char).
2. (3.2) Build and test an implementation of stacks that is like FiniteStack.T but which uses pointers to nodes which contain references to objects, to implement the storage for a stack that need not be finite.
3. (3.4) Give the public and private interface files that define a class FiniteStack.T which is a subclass of Collection.T. Be sure to include all methods required for stacks, all methods which are inherited and must be overridden, and an associated class FiniteStack.Iterator with all of its required parts. Give definitions of all of the methods used. For example what is the meaning of FiniteStack.T insert? Also be certain to define the appropriate generator function.
4. (3.4) Apply the dynamic binding principle to the following situation. Suppose you have built a "graphical figure" class that includes a method "draw." Its implementation is to call another method "vertices" that returns a list of the vertices (points) of the smallest rectangle with horizontal and vertical sides containing the figure. Draw then proceeds to draw lines from each vertex to the next in the returned list, finishing by drawing a line from the last vertex to the first. Thus, draw always draws a rectangle: the boundary rectangle of a figure. Next, suppose you build a new subclass of "graphical figure" called "five point star" You give it a new vertices method which returns the 10 points in order representing the five outer and the five inner intersections of the edges of a five point star. You do not implement a new draw method.
Now, suppose that you create a five point star and send it a draw message. Which version of vertices will be called by draw? The one that was originally created in the same class in which the draw method was created, or the one created in the new class that inherits the draw method? What will be drawn?
5. (3.4) a) How does the dynamic binding principle increase the flexibility of an implementor of a class?
b) The dynamic binding principle must be wisely used so that software becomes easier to build and use rather than harder. In light of this, what must implementors of override methods consider and what must they do?
c) Discuss the importance of stating preconditions and postconditions. Discuss the importance of adhering to preconditions and postconditions when we program.
6. (3.4) Explain the relationship between methods, the procedures that implement them, and the dynamic binding principle.
7.
8. (3.5) Implement the methods of class Magnitude.T except for hash, equal and less. Use these last two methods in your implementations.
9. (3.6) When we have a class B that "isLike" another class A rather than "isA" A we prefer not to implement B as a subclass of A but, perhaps, to implement B using an instance variable whose type is A. This is true even when we must write more code to do it this way. Why is this? To make the question more concrete, consider that a "set" isLike a "list" since they are both storage classes (collections) and that anything that we want to do with sets we can do with lists. Why don't we want to implement sets as a subclass of lists, but (perhaps) to implement sets using an instance variable that is a list?
10. (3.6) a) Implement FiniteStack.T from this Chapter.
b) Now build Fraction.T as discussed in this chapter.
c) Create some Fraction.Ts and one FiniteStack.T and push the fractions onto your stack.
d) Write out the stack using writeIt.
11. Build and test the following. It uses class Stack.T that is discussed in Chapters 4 and 7. We create a class Expression of data objects to insert into a stack.
MODULE Main;
IMPORT Object, Collection, Stack, Wr, Fmt, Stdio;
TYPE
Expression = Object.T OBJECT
fLeft, fRight: INTEGER;
METHODS
initExpression (a,b: INTEGER): Expression := InitExpression;
simplify() := Simplify;
OVERRIDES
writeIt := WriteIt;
END;
VAR
s: Stack.T;
IT: Collection.Iterator;
o: REFANY;
e1,e2,e3: Expression;
PROCEDURE InitExpression(self: Expression; a,b: INTEGER): Expression =
BEGIN
self.fLeft := a;
self.fRight := b;
RETURN self;
END InitExpression;
PROCEDURE WriteIt(self: Expression; f: Wr.T) =
BEGIN
IF fLeft = 0 THEN Wr.PutText(f, Fmt.Int(self.fRight));
ELSIF self.fRight = 0 THEN Wr.PutText(f, Fmt.Int(self.fLeft));
ELSE
Wr.PutText(f, Fmt.Int(self.fLeft));
Wr.PutChar(f, '+');
Wr.PutText(f, Fmt.Int(self.fRight));
END;
END WriteIt;
PROCEDURE Simplify(self: Expression) =
self.fLeft := self.fLeft + self.fRight;
self.fRight := 0;
END Simplify;
PROCEDURE NewExpression(a := 0; b := 0) =
VAR result: Expression;
BEGIN
result := NEW(Expression);
Object.FailNil(result);
EVAL result.initExpression(a,b);
RETURN result;
END NewExpression;
BEGIN
e1 := NewExpression (1,2);
e2 := NewExpression (3,4);
e3 := NewExpression ();
s := NewStack();
s.push(e1);
s.push(e2);
s.push(e3);
s.writeIt(Stdio.stdout);
Wr.PutChar(Stdio.stdout, '\n');
IT := s.newIterator();
(* Simplify all expressions in s. *)
WHILE IT.nextItem(o) DO
NARROW(o, Expression).simplify();
END;
s.writeIt(Stdio.stdout);
END Main.
12. Build and test the following modification of the code in Exercise 11. It derives the class SExpression from a simpler class STerm. It also pushes three of these objects onto a stack and manipulates them while they are in the stack. Be sure you understand which simplify and writeIt methods are being called. You might want to output the name of the class whenever a simplify or writeIt method is called. You can put a line like
cout << "STerm::simplify";
into the simplify method of STerm and a similar one into that of SExpression.
MODULE Main;
IMPORT Object, Collection, Stack, Wr, Fmt, Stdio;
TYPE
Term = Object.T OBJECT
fLeft: INTEGER;
METHODS
initTerm (a: INTEGER): Expression := InitTerm;
simplify() := SimplifyTerm;
OVERRIDES
writeIt := WriteTerm;
END;
Expression = Term OBJECT
fRight: INTEGER;
METHODS
initExpression (a: INTEGER): Expression := InitExpression;
simplify() := SimplifyExpression;
OVERRIDES
writeIt := WriteExpression;
END;
VAR
s: Stack.T;
IT: Collection.Iterator;
o: REFANY;
e1,e2,e3: Term; (* Note the change of types from Exrecise 3.11 *)
(* Term **********************************************)
PROCEDURE InitTerm(self: Expression; a,b: INTEGER): Expression =
BEGIN
self.fLeft := a;
RETURN self;
END InitExpression;
PROCEDURE WriteTerm(self: Expression; f: Wr.T) =
BEGIN
Wr.PutText(f, Fmt.Int(self.fLeft));
END WriteTerm;
PROCEDURE SimplifyTerm(self: Expression) =
(* Nothing. *)
END SimplifyTerm;
PROCEDURE NewTerm(a := 0) =
VAR result: Term;
BEGIN
result := NEW(Term);
Object.FailNil(result);
EVAL result.initTerm(a);
RETURN result;
END NewTerm;
(* Expression **********************************************)
PROCEDURE InitExpression(self: Expression; a,b: INTEGER): Expression =
BEGIN
EVAL self.initTerm(a);
self.fRight := b;
RETURN self;
END InitExpression;
PROCEDURE WriteExpression(self: Expression; f: Wr.T) =
BEGIN
IF fLeft = 0 THEN Wr.PutText(f, Fmt.Int(self.fRight));
ELSIF self.fRight = 0 THEN Wr.PutText(f, Fmt.Int(self.fLeft));
ELSE
Wr.PutText(f, Fmt.Int(self.fLeft));
Wr.PutChar(f, '+');
Wr.PutText(f, Fmt.Int(self.fRight));
END;
END WriteExpression;
PROCEDURE SimplifyExpression(self: Expression) =
self.fLeft := self.fLeft + self.fRight;
self.fRight := 0;
END SimplifyExpression;
PROCEDURE NewExpression(a := 0; b := 0) =
VAR result: Expression;
BEGIN
result := NEW(Expression);
Object.FailNil(result);
EVAL result.initExpression(a,b);
RETURN result;
END NewExpression;
BEGIN
e1 := NewExpression (1,2);
e2 := NewExpression (3,4);
e3 := NewTerm (6);
s := NewStack();
s.push(e1);
s.push(e2);
s.push(e3);
s.writeIt(Stdio.stdout);
Wr.PutChar(Stdio.stdout, '\n');
IT := s.newIterator();
(* Simplify all expressions in s. *)
WHILE IT.nextItem(o) DO
NARROW(o, Expression).simplify();
END;
s.writeIt(Stdio.stdout);
Wr.PutChar(Stdio.stdout, '\n');
IT.reset();
(* Write the stack by iterating over its contents. *)
WHILE IT.nextItem(o) DO
NARROW(o, Expression).writeIt(Stdio.stdout);
Wr.PutChar(Stdio.stdout, '\n');
END;
END Main.