He had a very curious collection of scarabees.
Evelyn, Diary (1827)
A great man...even in the magnitude of his crimes, finds a rescue from
contempt.
Junius, Letters
In this chapter we shall describe the data abstractions in our class hierarchy. We will not discuss implementations of the classes, but only the abstractions on which the classes depend, and the protocol of each class. In this way the classes may be used to build sophisticated programs, even without examining the details of the implementation. The reader could proceed from this chapter immediately to the applications later in the book. Alternatively, as the implementations are discussed in following chapters, the reader could examine them next. We will discuss two applications in the next chapter, which illustrate both collection and magnitude classes. Beginning in Chapter 6 we shall discuss these abstractions in detail.
For each abstraction we shall discuss the main idea on which its class depends, and the major methods that the class provides to its clients. We shall not discuss implementations here and so our class declarations are incomplete. We won't even show most of the instance variables at this time. We shall also not show or discuss some methods that are private to the implementation because they are not properly part of the specification and are of little help in learning to use these classes.
This chapter contains a lot of detail. It is probably better browsed than read completely from end to end. It serves as a collection of the protocols of the various classes for a user of the library.
Notice, as you browse this chapter, that we sometimes use the name of an interface as if it were the name of its major class. For example, we might refer to Object as the name of the interface, which is accurate, or use Object to refer to the class Object.T, the class exported from interface Object.
The complete hierarchy is shown in Figure 4.7 at the end of this chapter.
Every class actually used to create objects in this library is a subclass of Object.T, which is an abstract class. As shown above it implements basic functionality that we always want. The major subclasses of Object.T are Collection.T and Magnitude.T. There are a number of others, though most of them are associated in one way or another with either some collection class or some magnitude class.
We include the methods of Object here for reference. They are discussed in the previous chapter.
INTERFACE Object;
IMPORT Wr;
EXCEPTION fatal;
TYPE T = OBJECT
METHODS
writeIt(f:Wr.T) := WriteIt;
assert(a:BOOLEAN) RAISES {fatal} := Assert;
free() := Free;
shallowClone():T := ShallowClone; (* DO NOT OVERRIDE *)
clone():T := Clone;
copyFields(o:T) := CopyFields;
equal(o:T):BOOLEAN := Equal;
END;
PROCEDURE Error(s:TEXT) RAISES {fatal};
PROCEDURE FailNil(o:REFANY) RAISES {fatal};
PROCEDURE WriteIt(self:T; f:Wr.T);
PROCEDURE Assert(self:T;a:BOOLEAN) RAISES {fatal};
PROCEDURE Free(self:T) ;
PROCEDURE Equal(self:T; o:T):BOOLEAN ;
PROCEDURE ShallowClone(self:T):T ;
PROCEDURE Clone(self:T):T ;
PROCEDURE CopyFields(self:T; o:T) ;
PROCEDURE DoWrite(f:Wr.T; o:REFANY);
PROCEDURE AreEqual(m,n: REFANY):BOOLEAN;
END Object.
Magnitudes provide a notion of size. Magnitudes are objects that may be compared using less and its siblings. Most of the major subclasses of Magnitude.T are familiar: characters, strings, and various numeric types. Additionally there is an important subclass Association.T which is built on the idea of a key-value pair. Recall that Magnitude.T inherits equal from Object.T. The class Magnitude.T has public protocol:
INTERFACE Magnitude;
IMPORT Object, Wr;
TYPE
T = Object.T OBJECT
METHODS
less(m:T):BOOLEAN ;
hash():CARDINAL;
notEqual(m:T):BOOLEAN := NotEqual;
greater(m:T):BOOLEAN := Greater;
lessEqual(m:T):BOOLEAN := LessEqual;
greaterEqual(m:T):BOOLEAN := GreaterEqual;
between(first:T; second:T):BOOLEAN := Between;
min(m:T):T := Min;
max(m:T):T := Max;
OVERRIDES
writeIt := WriteIt;
equal := Equal;
END;
PROCEDURE NotEqual(self: T; m:T):BOOLEAN ;
PROCEDURE Greater(self: T; m:T):BOOLEAN ;
PROCEDURE LessEqual(self: T; m:T):BOOLEAN ;
PROCEDURE GreaterEqual(self: T; m:T):BOOLEAN ;
PROCEDURE Between(self: T; first:T; second:T):BOOLEAN ;
PROCEDURE Min(self: T; m:T):T ;
PROCEDURE Max(self: T; m:T):T ;
PROCEDURE WriteIt(self:T; f: Wr.T) ;
PROCEDURE Equal(self: T; o:Object.T):BOOLEAN ;
END Magnitude.
The first subclass of Magnitude (actually Magnitude.T, of course) that we discuss is Character.T. It gives us a way to treat elements of the built in type CHAR as if they were objects. This is often useful and necessary when we use collections of objects and want to use them to collect simple things. For example, in our class FiniteStack, defined above, we have a stack of objects. Many applications will want to stack characters (or integers, or strings, etc.) This class gives us the means to do this for character data. The essence of characters is that they can be displayed as ordinary text and can be composed into strings. They also form an ordered type so they can be compared for "size" with less. Since Character.T is a subclass of Magnitude.T, we must override the required methods less and equal. We also want to include a writeIt method which will write out the value of a Character. Notice however that this interface does not give the actual declaration of the class Character.T, but only indicates that this class is to be a subclass of the class Character.Public, which is itself a subclass of Magnitude.T. Thus we may assume that a Character.T object has all of the protocol of the classes Object.T, Magnitude.T, and Character.Public.
INTERFACE Character;
IMPORT Object, Magnitude;
TYPE
T <: Public;
Public = Magnitude.T OBJECT
METHODS
value():CHAR;
(* Returns the character value of self. *)
asText():TEXT;
(* Returns a textual value of self. *)
cat(t:TEXT):TEXT;
(* Append self to the beginning of t and return the result. *)
END;
PROCEDURE AsCharacter(ch:CHAR): T;
END Character.
We have a generator function AsCharacter (rather than Character.New) which returns a Character.T equivalent to the parameter that it is sent. This discrepancy is caused by the fact that the characters form a fixed set. We don't create characters. They exist. We simply get a reference to one of the standard characters with a call to AsCharacter. Two separate calls of AsCharacter(`A') will return two references to the same object. As there is only one character `A', there should be only one Character.T equivalent to it. The method value is the inverse of AsCharacter, returning a character value for the object.
The next class, Strings.T, is just a wrapper class to package the built in type TEXT. Our library requires that we use objects of type Magnitude.T in some places, such as in keys of Association.T objects, and TEXT objects don't fulfil that requirement. We use the interface name Strings rather than String, because the standard library has an interface named String and we don't want to interfere with a users ability to use it. A Strings.T represents a catenation of characters like a word, sentence or paragraph. We create new strings as we need them using String.New with an existing TEXT value. We retrieve the TEXT value using method value.
INTERFACE Strings;
IMPORT Object, Magnitude;
(* This is a simple packager of TEXTs as Magnitudes so that they can be used
as the keys of Associations. The details are public since TEXTs are not
updatable. *)
TYPE
T = Magnitude.T OBJECT
fValue: TEXT;
METHODS
initStrings(t: TEXT): T := InitStrings;
value():TEXT := Value;
OVERRIDES
less := Less;
equal := Equal;
hash := Hash;
writeIt := WriteStrings;
copyFields := CopyStringsFields;
END;
PROCEDURE Less(self: T; m: Magnitude.T):BOOLEAN;
PROCEDURE equal(self: T; o: Object.T):BOOLEAN;
PROCEDURE Hash(self: T): CARDINAL ;
PROCEDURE Value(self: T): T ;
PROCEDURE InitStrings(self: T; t: TEXT): T ;
PROCEDURE WriteStrings(self: T; f: Wr.T) ;
PROCEDURE CopyStringsFields(self: T; o: Object.T) ;
PROCEDURE New(t: TEXT): T;
END Strings.
The next class implements the abstract notion of a key and an associated value. Within any system keys are considered to be unique. The purpose of a key is to give access to the associated value. An example of a key value pair is a social security number (key) and a person's employment information (value). If the keys within some system are not unique we will not get access to a single data value, but to a collection. Associations are used as the basis of a dictionary, which is just a set of associations. Dictionaries (see the interface Dictionary) give a way to store information simply and to retrieve it efficiently. We shall use dictionaries when we build finite automata in Chapter 5. The public protocol follows. We inherit from Magnitude.T. The idea is that an association is an ordered pair where the first slot is filled with a magnitude. The second slot may be any reference value. Inherited methods less and equal use these keys in the first slot as the basis of the comparisons, ignoring the second, or value, slot.
INTERFACE Association;
IMPORT Magnitude;
TYPE
T <: Public;
Public = Magnitude.T OBJECT
METHODS
key(): Magnitude.T;
(* Return the key of the association. *)
value(): REFANY;
(* Return the value of the association. *)
setValue(o: REFANY);
(* Set the value of the assoication to o. *)
END;
PROCEDURE New(k: Magnitude.T; v: REFANY): T;
END Association.
One use of a dictionary would be to create a graph (a geometric figure composed of vertices connected by arcs). Each vertex in the graph could maintain a dictionary in which the associations would hold some unique key representing an arc incident at that vertex, and a value which is a reference to the vertex at the other end of that arc. Either the keys could be some natural feature of the application or could, artificially, be just a numbering of the arcs emanating from the vertex. Such a representation would have both advantages and disadvantages. It is important to note that this representation "distributes" the information about the graph to the vertices, rather than holds it all in one place. The information about the neighbors of a vertex is stored at that vertex, rather than having global information about the entire graph held centrally.

We have the usual generator function Association.New, which returns to us a fresh, properly initialized association with the given key and value. We also inherit the usual magnitude methods. We also have methods to get the key and the value of any association or to set a value. Note that changing the key of an association will not change its identity.
It is important to note that the comparison methods of associations depend only on the keys stored in them; the values are completely ignored for purposes of comparison. Thus, if two associations have the same key then they will be equal though they will not be "=". Thus to say
IF anAssociation = anotherAssociation THEN ...
is different from saying
IF anAssociation.equal(anotherAssociation)THEN ...
By our rule, using an informal syntax, (a,b) and (a,c) are equal since they have equal keys, but they are certainly not identical, and hence not "=". To emphasize this further, if we have two object reference variables A and B, then A = B will be true only when A and B are aliases of the same object. However the truth of A.equal(B) depends on the meaning of the method equal in the class of A. The default meaning of equal is "=" however, as this is how equal was defined in Object.T.
When choosing whether to use "=" or "equal," the second form is nearly always the correct one. The first one is true only if the two names are aliases or references to the same object. This is sometimes called for when implementing collections of associations, but not often used otherwise. The key idea to remember is that the class itself is supposed to know what it means for its elements to be equal and so the programmer most often uses the second, "equal," form to let the class be the judge.
There is another similar class, IdentityAssociation.T, with the same protocols as Association.T except that equality is based on identity. In other words for two identity associations to be equal, the keys of both must be identical to each other and the values identical as well.
Pairs, though not magnitudes, are shown here for completeness. They are like associations, except the keys are not assumed to be unique. For this reason equality of pairs is dependent on both the key and the value. Pairs are just the "ordered pairs" of mathematics. The class Pair.T encapsulates this. Two members of the class are equal if their keys are "=" and also their values (recall that = means identical). A set of pairs can be used to implement a "relation", while a set of associations (a dictionary) actually implements a function. Here we have only a generator of new Pairs. This class is completely abstract, since all we know of it is that it is some subclass of Object.T.
INTERFACE Pair;
IMPORT Object;
TYPE
T <: Public; (* An ordered pair of an object and a REFANY *)
Public = Object.T OBJECT
METHODS
key(): Object.T;
value(): REFANY;
END;
PROCEDURE New(k: Object.T; v: REFANY): T;
END Pair.
The next class, Numeric.T, will not be implemented. Therefore it is actually a pseudo class. We include it here to show the protocol of all of the numeric classes Integer.T, Fraction.T, Real.T, Complex.T, and LargeInteger.T. If Modula-3 were not strongly typed, requiring typing of all method parameters, then we would include this class. As it is, we exclude it, except from our documentation, as we have more control over types if we exclude it. The numeric classes all have arithmetic operations in addition to the comparisons of magnitudes.
TYPE Numeric = Magnitude.T OBJECT
METHODS
add (b: Numeric);
(* Return the "sum" of self and b. Meaning depends on class of self. *)
subtract(b: Numeric);
multiply(b: Numeric);
divide(b: Numeric);
END;
The four methods implement the ordinary arithmetic operations. In the actual classes which are "pseudo subclasses" of this pseudo class, our parameters will always be elements of the specific subclass. In addition to these methods, each actual class will also provide a means of dealing with information specific to that numeric type. For example Complex.T could provide a method imaginaryPart to return the imaginary part of itself.
We have seen Fraction.T above. The class implements ordinary fractions reduced to lowest terms. It provides all of the Numeric methods, as well as the inherited Magnitude methods.
INTERFACE Fraction;
IMPORT Object, Magnitude;
TYPE
T <: Public;
Public = Magnitude.T OBJECT
(* INVARIANT: Denominator is always positive.
Fraction is always lowest terms. *)
METHODS
add(f: T):T;
(* Compute the sum of self and f and return it. *)
subtract(f: T):T;
(* Compute the difference of self and f and return it. *)
multiply(f: T):T;
(* Compute the product of self and f and return it. *)
divide(f: T):T;
(* Compute the quotient of self and f and return it. *)
END;
PROCEDURE New(n,d: INTEGER):T; (* Return 0 if d=0 *)
END Fraction.
We won't show a complex number class in this book, leaving it as an exercise. Its protocol is suggested by the above, and its implementation is similar to that of Fraction.T as well.
The integer class, Integers.T, is like Character.T since it implements a fixed set of integers. A Integers.T object is a 32 bit (or larger) integer stored as an object. It is a Magnitude and also a Numeric. We won't create new Integers with new, but will generate references to the standard set of integers instead. Integers aren't created. They "exist." The implementation will need to be clever so as not to try to store all four billion or so possible values, and yet behave as if they were all available. Again we use Integers.T, rather than the preferred Integer.T, to avoid conflict with a standard interface name.
INTERFACE Integers;
IMPORT Magnitude;
TYPE
T <: Public;
Public = Magnitude.T OBJECT
METHODS
value(): INTEGER;
(* Return the INTEGER value of self. *)
add(o: T): T;
subtract(o: T): T;
multiply(o: T): T;
divide(o: T): T;
mod(o: T): T;
(* Return self modulo o. *)
END;
PROCEDURE AsInteger(i: INTEGER):T;
END Integers.
Another class that we won't build here is Real.T. The idea is the same as that of Integers.T, and its implementation could be similar as well. The protocol, except for the names would be the same as that of Integer, unless special methods were needed. The details are left to exercises.
The last magnitude class that we shall discuss is LargeInteger.T. It is like Integers.T, except that as implemented it permits the use of forty digit integers. A different implementation could easily permit even larger integers to be represented easily (if slowly).
INTERFACE LargeInteger; (* Assumes 32 bits for INTEGER *)
IMPORT Object;
TYPE
T <: Public;
Public = Magnitude.T OBJECT
METHODS
add(o: T): T;
subtract(o: T): T;
multiply(o: T): T;
divide(o: T): T; (* returns NIL on divide by zero *)
mod(o: T): T;
sign():Boolean; (* positive = TRUE *)
increment(b: T);
(* Add b to self. *)
decrement(b: T);
(* Subtract b from self. *)
negated(): T;
(* Return a value with same magnitude as self but opposite sign. *)
negate();
(* Change the sign of self. *)
isZero():BOOLEAN;
(* True if self = 0 (or -0). *)
END;
VAR overflow: BOOLEAN;
PROCEDURE NewLargeInteger(sign := positive; p9:=0; p8:=0; p7:=0;p6:=0 p5:=0;
p4:=0; p3:=0; p2:=0; p1:=0; p0:=0):T;
END LargeInteger.
Most of these methods should be familiar. Note that increment changes the object which receives the message, while add does not. Add simply returns the sum. Negated returns a new large integer equal to the negative of the receiver, while negate changes the sign of the receiver.
The implementation of this class is as base 10000 integers stored in an array. NewLargeInteger has parameters for the sign of the value as well as the ten "digits" of this representation. As a result each of these latter parameters should be in the range of 0 through 9999. Note that default values are provided for all parameters. If INTEGER is larger than 32 bits on your computer, it would be advantageous to reimplement this class to take advantage of the fact, though this class will still work correctly there.
We have seen the collection and iterator classes above when we looked at finite stacks. Collections are one of the richest of abstractions. In fact most of them require us to develop groups of abstractions, since collections are linked to iterators. Collections differ in the amount of structure internal to the collection as well as in the type of object which may be collected. Some classes for example, only permit us to collect magnitudes. SortedList is an example of this, as is BinarySearchTree. Sometimes we use an implementation which imposes restrictions. A Set, for example, may hold any sort of reference, and imposes no structure on the values in it. A similar class externally is BSTSet, which also implements a set, but its implementation, while more efficient, requires that the objects in it be in some subclass of Magnitude.
Some collection classes have a well defined notion of a "position" in the collection. This is the case with Lists.T, and with all tree classes. These classes are called indexed collections, and we shall have a pseudo class IndexedCollection to account for this. We shall also have another associated abstraction Position, for each such class. In some classes the notion of position is an ordinal position: first, second, etc. These are the arrayed collections. Still others impose an order on the contents which is derived from the values of the contents themselves. These are the ordered collections, such as BinarySearchTree.T. They require that their contents be in Magnitude.T. If the physical order within the collection is the same as the natural order of the contents then the collection is a sortedCollection, as is SortedList.T. It is instructive to see the entire hierarchy at once, so we present it below. Indentation shows inheritance here, so that a DEQueue is a Queue which is a List which is a Collection. (Note that there are a few inaccuracies in the list below. Our implementations will actually be a little different, with some of the classes using an implementation dependent on some of the others.
Collection
Set {finite set of objects}
Dictionary {set of associations-- key-value pairs}
HashDictionary {hash table implementation}
Bag {a multi-set. multiple inclusion possible}
IndexedCollection {collection with position-- Pseudo Class}
Lists
Queue
DEQueue {double ended queue}
Stack
Tree {a general tree}
BinaryTree
ArrayedCollection {position is an integer-- Pseudo Class}
DynamicArray {very large arrays-- dynamic arrays}
FixedSizeCollection {not expandable-- Pseudo Class}
Interval
Array
OrderedCollection {-- Pseudo Class}
{collection of magnitudes, kept partially ordered}
Heap
BinarySearchTree
AVL Tree
234 Tree
BTree
BSTSet {a binary search tree implementation of a set}
SortedCollection {imposes total order on contents
-- Pseudo Class}
SortedList
All of these classes are associated with corresponding iterator classes. Iterators provide generalized repetition operators for any collection class. Most iteration classes have the same protocol. A few provide several different forms of repetition. Thus there is a parallel hierarchy to the one shown above, which matches an iteration class to every collection class.
The following three classes are defined in Collection.i3, which also defines the Position class.
INTERFACE Collection;
IMPORT Object;
TYPE (* Three Abstract Classes: Collection.T, Iterator, and Position *)
ActionProc = PROCEDURE(o: REFANY);
TransformProc = PROCEDURE(o: REFANY):REFANY;
PredicateProc = PROCEDURE(o: REFANY):BOOLEAN;
T = Object.T OBJECT (* Collection of REFANY objects *)
METHODS
insert(o:REFANY) ; (* := NIL *)
(* Insert o into self. *)
remove(o:REFANY) ; (* := NIL *)
(* Remove o from self if present. *)
newIterator():Iterator ;(* := NIL *)
eachDo(DoIt:ActionProc) ;(* := NIL *)
(* apply DoIt to each element of self. *)
firstThat(checkIt:PredicateProc):REFANY := FirstThat;
(* Return the first value for which checkIt returns TRUE. *)
select(c:T; checkIt:PredicateProc) := Select;
(* Insert any element e into c if checkit(e) returns TRUE. *)
reject(c:T; checkIt:PredicateProc) := Reject;
(* Insert any element e into c if checkit(e) returns FALSE. *)
collect(c:T; transformIt:TransformProc) := Collect;
(* Insert transformIt(e) into c for each element e in self. *)
empty():BOOLEAN := Empty;
(* Return TRUE if self is empty. *)
element(o:REFANY):BOOLEAN := Element;
(* Return TRUE if o is in self. *)
cardinality():INTEGER := Cardinality;
(* Returns the size of the collection. *)
OVERRIDES
writeIt := WriteIt;
END;
PROCEDURE FirstThat(self:T; checkIt:PredicateProc):REFANY ;
PROCEDURE Select(self:T; c:T; checkIt:PredicateProc) ;
PROCEDURE Reject(self:T; c:T; checkIt:PredicateProc) ;
PROCEDURE Collect(self:T; c:T; transformIt:TransformProc) ;
PROCEDURE Empty(self:T):BOOLEAN ;
PROCEDURE Element(self:T; o:REFANY):BOOLEAN ;
PROCEDURE Cardinality(self:T):INTEGER ;
PROCEDURE WriteIt(self:T; f: Wr.T) ;
TYPE
Iterator <: PublicIterator;
PublicIterator = Object.T OBJECT
METHODS
initIterator(c: T): Iterator;
nextItem(VAR o: REFANY):BOOLEAN ; (* := NIL *)
(* If all items have been yielded then return FALSE. Otherwise return TRUE
and set o to the next unyielded item of self. *)
reset() ; (* := NIL *)
(* Reset to the beginning as if no elements had yet been yielded. *)
short();
(* Short-circuit the iterator so that nextItem will next return FALSE. *)
done():BOOLEAN;
(* TRUE if all items have been yielded (or none were initially present). *)
END;
Position <: PublicPosition;
PublicPosition = Object.T OBJECT
METHODS
initPosition(c: T):Position;
reset() ; (* := NIL *)
(* Reset self the the "first" position of its collection. *)
END;
END Collection.
All subclasses of the pseudo class IndexedCollection are associated with a corresponding position class. Thus there is a class Lists.Position, and another BinaryTree.Position. We have a class Collection.Position to form the head of the hierarchy of position classes. It doesn't do much, as the details of a position depend too much on the nature of the indexed collection that they correspond to. Note, however, that a position is always associated with a given collection.
Collections may collect any type of reference. Thus we may insert any REFANY value into a collection. Method empty tells us if the receiver collection is empty and element tells us whether a given value is currently present in the collection. cardinality gives the numeric count of the elements in the collection.
We have two types of iterators shown in this interface. The first is the class Collection.Iterator, which has a method nextItem to return the objects in a collection to us, one at a time, so that an operation may be performed on each (or only on some) of them. These kind of iterators are called "external interators" because they are implemented as objects separate from the collections over which they iterate. They are always associated with a particular collection. Once this association is made, it cannot be changed.
The other kind of iterator, "internal iterators" are represented by the methods eachDo, firstThat, select, reject, and collect of the Collection.T class itself. These apply some operation, represented as a procedure or function supplied as a parameter to the method itself, to each of the elements of the collection. eachDo, applies its action procedure to every element. Function firstThat returns the first element of the collection that meets the criteria of its predicate procedure . Method select will apply its predicate procedure to every element of the collection and those that meet the criteria (return TRUE) will be inserted into the Collection.T parameter. Likewise reject will insert all those values that return FALSE when the predicate procedure is applied. Finally, collect applies the transform procedure to each of the elements, and inserts the results into the Collection.T parameter.
The simplest collection is a set. We are striving for a mathematicians idea of a set. Sets contain values (actually REFANY references). A value can be an element of a set or not. Multiple inclusion is not meaningful or possible. Inserting a value into a set which already contains it is a no-op (no operation is performed). Sets can also be heterogeneous and contain values of different types. We inherit the insert and remove operations, of course, and add methods to perform common set operations such as union and intersection. Method allBut returns a new set that does not contain the parameter. It is like remove, except that it doesn't modify the receiver, but returns a new set instead. Note that Set.T inherits method newIterator from Collection.T. This method is is the generator function for objects of class Iterator.
INTERFACE Set;
IMPORT Collection;
TYPE
T <: Public;
Public = Collection.T OBJECT
METHODS
union(s: T): T;
(* Return the set union of self and s. *)
intersection(s: T): T;
(* Return the intersection of self and s. *)
allBut(o: REFANY): T;
(* Return a set like self, but without o present. *)
subset(s: T): BOOLEAN;
(* TRUE if self is a subset of s. *)
END;
PROCEDURE New(): T;
END Set.
A bag is one of the most general collection mechanisms. It is called a multi-set by mathematicians. A bag is like a set except that multiple inclusion is possible. Therefore, when an object is removed from a bag it may still be in the bag. Their protocol is like that of a set.
INTERFACE Bag;
IMPORT Set;
TYPE
T <: Set.T;
PROCEDURE New(): T;
END Bag.
Dictionaries were discussed above when we introduced associations. A dictionary is just a set of associations. Associations are key-value pairs. Thus a dictionary is a simple data base, maintaining information (value) for us which is retrievable at will (via the key). A hash dictionary is similar, differing in the implementation. Another way to think of a dictionary is that it implements a function, with the keys being the domain and the values representing the range.
INTERFACE Dictionary;
IMPORT Set, Magnitude;
TYPE
T <: Public;
Public = Set.T OBJECT
METHODS
atPut(k: Magnitude.T; v: REFANY);
(* If self has no element with key k, then create a new association (k,v) and
insert it. Otherwise set the value of the association with key k to v. *)
at(k: Magnitude.T): REFANY;
(* If self has an element with key k then return the associated value.
Otherwise return NIL. *)
keyAtValue(v: REFANY): Magnitude.T;
(* If self has an element with value v then return the associated key.
Otherwise return NIL. *)
removeKey(k: Magnitude.T);
(* Remove the element with key k if present. *)
END;
PROCEDURE New(): T;
END Dictionary.
The method atPut is the basic insert operation into a dictionary. It sees to the creation of the association which will store the key and the value. Actually, no creation may be necessary. If the key is already contained in the dictionary, then atPut simply changes the value of the stored association to the new value given. Likewise at is the method by which we get access to the value from the given key. Note that it does not remove anything from the dictionary. Only removeKey will do that. It removes the association with the given key. The inherited insert may be used to insert an association into a dictionary if it was created externally. Note that if it has a key equal to the key of any association already in the dictionary this is a replacement operation.
The class Lists.T is one of the more complex classes in the entire hierarchy. This is because it is linked to three other classes: Lists.Node, which implements the storage of a single data item; Lists.Position, which gives us an abstract notion of position in the list; and List.Iterator, which lets us perform some operation on every element of a list. The idea on which a list depends, is a linear or sequential structure which has a first member, and in which every member except the last member has a successor or next member. Each member of the list except the first and last is thus "related" to two others, the next item, and the previous item. There is no necessary relationship between the values of the data in the list and the position in the list. There is no necessary relationship between the order of insertion and the position. Multiple inclusions of the same object are possible.
Actually there are two ways to think about lists. The first is that a list is a collection of data items which are connected together into a linear structure.
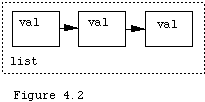
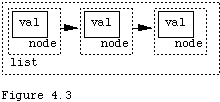
This view, if refined, distinguishes between the values in the list and the nodes which hold the values. Conceptually it is a list of values, as shown in Figure 4.2. From the implementation view it is a list of special objects called nodes and the nodes hold the data. See Figure 4.3. This is how we shall implement lists. Lists, values, and nodes all have their own behaviors, designed into their protocols. We shall permit the lists to contain any objects, and shall not restrict that values in a list be all of one kind. Applications which use lists often do impose such a restriction, but there is nothing in the idea of a list itself that all of its data must come from the same general class of items.
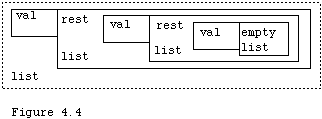
The second way of looking at lists is to consider that a list is either empty or it is a data value called "val", and a list called "rest". This definition is recursive. List was defined in terms of a (sub) list. The fact that a list may also be empty prevents the definition from degenerating into an infinite loop of definitions, which doesn't define anything. This idea is illustrated in Figure 4.4.
We shall prefer the first definition of lists, but show how the second may be defined and implemented in Chapter 7. The language LISP is actually built on the second idea of lists.
We are using nodes to implement lists, but they are not seen by clients, who are encouraged to think of lists as containing data, not nodes. Therefore we include the declaration of nodes in another interface PRLists.i3, that is not shown here. PRLists.Node is therefore completely private to an implementation. The implementations, and hence, the rest of the private details, will be shown in Chapter 6. Lists.Iterator and Lists.Position, being public, are defined here. Lists is a prime example of an Abstract Data Type (ADT) composed of several data abstractions. Here Lists.T is the primary abstraction, of course.
INTERFACE Lists;
IMPORT Collection;
TYPE
T <: Public; (* List of REFANY *)
Position <: PublicPosition;
Iterator <: Collection.Iterator;
WhereFound = {IsHere,IsNext,NotFound};
Public = Collection.T OBJECT (* List of Objects *)
METHODS
initList():T;
first(): REFANY;
(* Returns a reference to the first element in the list. *)
last(): REFANY;
(* Returns a reference to the last element in the list. *)
removeFirst();
(* Removes the first element in self, if any. *)
insertFirst(o: REFANY);
(* Insert o as the first element in self. *)
insertLast(o: REFANY);
(* Insert o as the last element of self. *)
removeLast();
(* Removes the last element of self. *)
newPosition():Position;
(* Returns a new position into self, initialized to the first element. *)
END;
PublicPosition = Collection.Position OBJECT
METHODS
next();
(* Move to the next position. *)
prev();
(* Move to the previous position unless at first position. *)
toLast();
(* Move to the last position. *)
insertFirst(o: REFANY);
(* Insert o as the first element of self and move there. *)
insertAfter(o: REFANY);
(* Insert o after the current position and before the current next. *)
at(): REFANY;
(* Return the value at this position. *)
atPut(o: REFANY);
(* Put a new value o into this position. *)
last():BOOLEAN;
(* TRUE if at the last position. *)
afterLast():BOOLEAN;
(* TRUE if current position is AFTER the last position, as in an empty
list. *)
deleteFirst();
(* Remove the first element in the list. *)
deleteNext();
(* Remove the next value after the current position (if any). *)
atNext(): REFANY;
(* Return the value in the next position or NIL if none. *)
search(o: REFANY):WhereFound;
(* Search for o from the current position. Returns:
isHere if the current position contains o
notFound if o cannot be found at or after the current position
isNext if we can move forware (or not at all) to the predecessor of a
position containing o, in which case we so move. *)
moveTo(p:Position);
(* Move to the same position as p. *)
exchangeValues(p:Position);
(* Swap the values at positions self and p. *)
END;
PROCEDURE New(): T;
END Lists.
Note that there isn't much here to let us manipulate a list other than at its beginning. There are two ways that such manipulation may be done. First, like all collections, lists have iterators. These may be used for operating on the list as a whole. The public protocol for a list iterator is identical to that of a collection iterator.
The second way to operate on a list is to create and use a list position. As lists are examples of the pseudo class IndexedCollection, we must create an abstraction for position in a list and then implement the abstraction. A list position is a reference to some item (data value actually) stored in the list. Positions may move forward or backward in the linear list structure, and operations may be applied at the "current location" of a position. The protocol is shown above.
All of these position methods maintain the view that we have a list of values. The protocol includes position movement methods such as toLast, and next. It includes last for determining if we are at the end. We also have at and atNext for retrieving data from the list and atPut, insertFirst, and insertAfter for inserting values. InsertAfter creates a new node to hold the data. It also changes the relative positions of all following nodes, increasing their ordinal positions in the list by one. We may delete values (and their nodes) with deleteFirst and deleteNext, which also change ordinal positions of the values in the list. MoveTo permits us to easily set one position to the location of another, which is useful in complex list manipulations, and exchangeValues exchanges the values in the nodes at the two positions (receiver of the message and the parameter) while leaving the nodes in place.
The user must be somewhat careful in using positions while otherwise changing a list. There are two ways to remove the first value in a list. One is with a message sent to a position, and the other is with a message sent to the list itself. The former method is safer, if positions are active, as it permits the position to update its internal data. Generally deletions and insertions into a list in which positions are active must be carefully thought out. reset is a method which can be sent to a position into a list and the position will reset itself to the first element. This is sometimes necessary when the list has just had its first element deleted, so that the position will be properly updated.
Note again that we have a generator function for lists. The generator functions for List.Iterator and List.Position are methods of List.T. This is in keeping with the idea that a list iterator always iterates over a specific list. You can't create a "free standing" list iterator.
Stacks, queues, and double ended queues (dequeues) are related to lists. They all have a sequential structure, and all are collections of objects. They differ in the protocol for insertion and deletion. Stacks, as we have seen before implement a LIFO protocol for insertions and deletions. The easy way to handle this is to keep the elements in the stack in a list and only permit insertions and deletions from one end. Our definition of pop has changed as it now returns an object as well as removing that object from the list. Queues implement a FIFO structure, in which the next item to be removed is the one that has been in the queue for the longest time. This is easily done by inserting at one end of a list and deleting at the other end. A dequeue (pronounced "deck", as in deck of cards, which is an example of a dequeue in fact) permits insertions and deletions at either end of a list but not otherwise. The formal rules for stacks have been discussed. We will discuss rules for queues and double ended queues in chapter 7.
INTERFACE Stack;
IMPORT Collection;
TYPE
T <: Public;
Public = Collection.T OBJECT
METHODS
push(o: REFANY);
(* Insert o onto the "top" of the stack. *)
pop(): REFANY;
(* Remove and return the item at the top of the stack. *)
top(): REFANY;
(* Return a reference to the item at the top of the stack. *)
END;
PROCEDURE New(): T;
END Stack.
INTERFACE Queue;
IMPORT Collection;
TYPE
T <: Public;
Public = Collection.T OBJECT
METHODS
enqueue(o: REFANY);
(* Insert o at the rear of the queue. *)
dequeue(): REFANY;
(* Remove and return the item at the front of the queue. *)
atFront(): REFANY;
(* Return a reference to the item at the front of the queue. *)
END;
PROCEDURE New(): T;
END Queue.
INTERFACE DEQueue;
IMPORT Object, Collection, Queue;
TYPE
T <: Public;
Public = Queue.T OBJECT
METHODS
insertFront(o:REFANY);
(* Insert o at the front of the dequeue. *)
removeRear():REFANY;
(* Remove and return the item at the rear of the dequeue. *)
atRear():REFANY;
(* Return a reference to the item at the rear of the dequeue. *)
END;
PROCEDURE New(): T;
END DEQueue.
Note that as collections they have access to iterators. Stacks, Queues and DEQueues will each implement the newIterator method, by actually returning a Lists.Iterator object, The protocol doesn't show it, of course, but we shall build each of these classes using lists. Note that a dequeue is a queue, and so most of the important methods are inherited. We must consider how to provide the iterator functionality to Stacks.
Stacks are used extensively to process any data that occurs in a nested manner. This permits us to handle a nested item (by pushing) and later return to the item that contained it (pop). We have given pop a different meaning here than we did in Chapter 2, since it is a function returning a value. Queues are used when items may be encountered in processing other items and we want to be sure that we get around to processing them all. We enque them when they are encountered, and dequeue an item when we are ready to handle a new one. They are also used in "service" systems, such a simulations, where we may need to process items repeatedly and we want to do it cyclically, providing equal opportunities for service to all of the objects.
Sortable lists keep their data in order. This requires special insert methods, and also requires that the data all be in Magnitude.T, or at least support a less method, for it is from here that we get the ability to compare sizes. This class will be implemented using a generic interface, where the interface parameter E (for Element) gives the class of the elements to be collected in the sorted list.
GENERIC INTERFACE SortableList(E);
IMPORT Lists;
(* REQUIRE: E.T <: ROOT and support method
less(e: E.T): BOOLEAN;
ALSO: Methods that do inserts only accept arguments of type E.T.
These include T.insert, T.insertFirst, T.insertLast, Position.insertFirst,
Position.insertAfter, Position.atPut;
*)
TYPE
T <: Public;
Public = Lists.T OBJECT (* Sortable List of E.T References *)
METHODS
selectionSort();
(* Sort self using the selection sort algorithm. *)
merge(list: T):T;
(* Merge self and list and return the result. Do not modify self or list. *)
END;
PROCEDURE New():T;
END SortableList.
This generic interface is defined in such a way that any class deriving from Magnitude.T will be acceptable as the parameter class. Therefore, as Integers defines a class Integers.T derived from Magnitude.T, we may create a concrete interface IntegerList from this generic interface by creating a file IntegerList.i3 that contains just the one line:
INTERFACE IntegerList = SortableList(Integers) END IntegerList.
Remember that a generic interface is just a template for creating actual interfaces. It is these actual interfaces that are compiled and linked to form a running program. A generic interface is of no use to us if we don't "instantiate" it.
Trees are important both because they arise naturally in a number of important application areas and because they offer an efficient implementation mechanism in many others. The syntax of a computer program is usually described by a tree, the parse tree, which offers an abstract representation of the static program. Compilers often construct this tree as part of translation. Even if they don't construct it directly they implicitly visit the nodes of the tree to determine if the program is valid. Trees can also be an efficient implementation mechanism for sets -- especially sets of magnitudes.
Trees are indexed collections and so have both positions and iterators. Trees also hold data in nodes. Unlike our treatment of lists, we will treat the nodes here more as first class citizens, partly because the shape of the tree, independent of the data, often carries information which is important. The simplest sort of tree is a binary tree and we shall implement the class BinaryTree.T. Binary trees are made up of nodes and links, with each node that is internal to the tree having exactly two children. These children are also binary trees. A node which is not internal is called external and it has no children. A node which has children is called the parent of those children. In binary trees we distinguish the children as the left and the right child respectively. We normally think of the children as being below the parent. The node with no parent is called the root of the tree.
We must be able to create trees and their nodes, insert, retrieve, and remove data, move about in the tree, and process the tree as a whole. Movement must be provided both upwards, towards the root, and downwards along the many paths from a node to the external nodes (leaves) below it. Recall that we hid the list node class within the private interface. We do the same here with the tree nodes, for the same reason. The protocols of BinaryTree.T, BinaryTree.Iterator, and BinaryTree.Position are shown below.
INTERFACE BinaryTree;
IMPORT Object, Collection;
TYPE
T <: Public;
Iterator <: PublicIterator;
Position <: PublicPosition;
Public = Collection.T OBJECT
METHODS
(* Note: Insert inserts a leftmost leaf. *)
newInOrderIterator():Iterator;
(* Note: newIterator returns a pre-order iterator. *)
newPosition():Position;
END;
PROCEDURE New(): T;
TYPE
PublicIterator = Collection.Iterator OBJECT
METHODS
nextItemInOrder(VAR o: REFANY): BOOLEAN ;
(* Note: nextItem returns the next item using pre-order. *)
iterateFrom(p: Position);
(* Iterate only from the node at position p. *)
resetInOrder();
(* Reset the iterator so it will properly iterate using in-order. *)
END;
FromDirection = {fromLeft, fromRight, noMove};
PublicPosition = Collection.Position OBJECT
METHODS
setToRoot();
(* Move to the root of the tree. *)
at():REFANY;
(* Return the item at the current position. *)
atPut(o: REFANY);
(* Insert value o into the current position. *)
atLeftChild():REFANY;
(* Return the value at the left child of the current position
(or NIL if none). *)
atRightChild():REFANY;
(* Return the value at the right child of the current position
(or NIL if none). *)
exchangePositions(p: Position);
(* Self and p will exchange positions. *)
exchangeValues(p: Position);
(* Self and p will swap values. *)
find(o: REFANY);
(* Search for o from the current position and move there.
No-op if not found. *)
leaf():BOOLEAN;
(* TRUE if current position has no children. *)
noLeft():BOOLEAN;
(* TRUE if current position has no left child. *)
noRight():BOOLEAN;
(* TRUE if current position has no right child. *)
oneChild():BOOLEAN;
(* TRUE if current position has only one child. *)
isFull():BOOLEAN;
(* TRUE if current position has two children. *)
missingNode():BOOLEAN;
(* TRUE if the position is not that of any data item: i.e. below a leaf. *)
moveTo(p: Position);
(* Make the position of self the same as that of p. *)
moveLeft();
(* Move to the left child if any. May move below a leaf. *)
moveRight();
(* Move to the right child if any. May move below a leaf. *)
moveToParent():FromDirection;
(* Move to the parent of the current position. No-op if at root. *)
isAtRoot():BOOLEAN;
(* TRUE if current position is at the root. *)
insertLeft(o: REFANY);
(* Insert o to the left. If the tree is empty this inserts the root. Otherwise
it assumes that the left child is missing--no-op otherwise. *)
insertRight(o: REFANY);
(* Insert o to the right. If the tree is empty this inserts the root. Otherwise
it assumes that the right child is missing--no-op otherwise. *)
END;
END BinaryTree.
Nearly all of the functionality is provided by positions and iterators. Tree positions let us move about in trees and do complex manipulations. They are similar to list positions except that the processing is complicated by the two children which "follow" any given node. We must be able to move to either child or to the parent. We have methods for movement, checking position, insertions of nodes and data, removals, retrievals, and searching.
Note that users must exercise caution when inserting a node into a tree. When the node is already in the tree the result is not a tree but a graph. It is even possible that the resulting graph will have cycles, so that repeatedly moving to a child will eventually bring you back to where you began. A "tree" with this property is not a tree at all and such an insert will make iterators fail. In fact they may loop infinitely.
Tree iterators are more complicated since it is often necessary to be specific about the order in which the iterator yields the nodes of a tree. For our purposes the two most important are preorder and inorder, and we provide methods so that an iterator may operate in either way. The preorder protocol requires that a node be yielded prior to its children, and that the left child be yielded before the right. This is called a top down traversal order. With inorder protocol, the left child of a node is yielded before the parent and the right child after the parent. As this is applied recursively, the first node yielded in inorder is one far down the left side of the tree. A third protocol, postorder (bottom up) yields the parent last. Our iterators don't have a bottom up protocol. We get a tree iterator as usual by sending the newIterator message to a tree. The method executed returns a properly initialized preorder iterator. The message newInOrderIterator returns an iterator initialized for inorder traversal.
There are times in which binary trees are not adequate for the application being developed. For this we need general trees, which permit an arbitrary number of children as in Figure 4.6.
All the tree operations (movement, retrieval, insertion, and deletion) are complicated by the presence of many possible children. Our implementation shall actually use binary trees, but the protocol must permit referencing the numerous children that a node may have.
INTERFACE Tree;
IMPORT Object, Collection;
TYPE
T <: Public;
Public = Collection.T OBJECT
METHODS
newPosition(): Position;
END;
PROCEDURE New(): T;
TYPE
Position <: PublicPosition;
PublicPosition = Collection.Position OBJECT
METHODS
setToRoot();
at():REFANY;
atPut(o: REFANY);
exchangePositions(p: Position);
exchangeValues(p: Position);
find(o: REFANY);
leaf():BOOLEAN;
noLeft():BOOLEAN;
noRight():BOOLEAN;
isFull():BOOLEAN;
missingNode():BOOLEAN;
moveTo(p: Position);
moveToParent(); (* different protocol than in BinaryTree.T *)
isAtRoot():BOOLEAN;
moveToChild(n: INTEGER);
(* Move to the n'th child of this parent. Can move "past" the last child. *)
insertChild(o: REFANY);
(* Insert a new "first" child of this position. *)
atChild(n: INTEGER):REFANY;
(* Return the value at the n'th child of this position, or NIL of none. *)
END;
END Tree.
Note that nothing new is added to the tree itself. We get the new functionality by changing the position abstraction. Here we may add a new child, independent of how many exist. The children are not ordered in any fixed way. moveToChild sets the position to the child currently in the ordinal position given by the parameter. The corresponding behavior in atChild returns the data in the current n'th child. Inserting a new child will change this ordinal position.
We will also show how to implement binary search trees. These are binary trees in which all of the data in the left child of any node is less than the data at that node, and all of the data in the right child is greater. This requires that the data all be in Magnitude.T or have equivalent protocol, so that we can apply the ordering operations. AVL trees , 234Trees, and BTrees are variations on the same theme. They form efficient ways to store sets of values and are useful in database applications. We shall again use a generic interface for binary search trees, similar to what we did for sortable lists.
GENERIC INTERFACE BinarySearchTree (E);
IMPORT Object, Collection, BinaryTree;
(* REQUIRE: E.T <: ROOT and it must support methods
equal(o: E.T):Boolean;
less(o: E.T):Boolean;
lessEqual(o: E.T):Boolean;
greaterEqual(o: E.T):Boolean;
ALSO: Insertion methods here require arguments of type E.T.
*)
TYPE
T <: BinaryTree.T;
PROCEDURE New(): T;
TYPE
Position <: PublicPosition;
PublicPosition = BinaryTree.Position OBJECT
METHODS
seek(o: E.T):BOOLEAN;
(* Move to position of o or to a leaf where o can be inserted *)
find(o: E.T);
(* Move to position of o only if it exists below current *)
END;
END BinarySearchTree.
A Heap is a similar structure, except that the ordering relationship is weaker. All that is required in a heap is that the data in any node be less that the data in both of its children. Thus size increases as you go down a tree and decreases as you go up. Heaps are very useful in implementing efficient sorting routines for data that will ultimately be held in sequential structures, as their smallest item of all is in the root. Notice that if we have a heap and then repeatedly remove the root, while maintaining the heap property we will gain access to the data in sorted order. The protocol will not be shown here as it is somewhat specialized.
One of the major difficulties with arrays is that they take up a lot of room if only a few of their elements are actually needed. There is a need for a mechanism like arrays which can be created an element at a time. This is our DynamicArray.T class. Conceptually, a dynamic array is like ARRAY[0..maxSize-1] of REFANY, except that we can change maxSize at run-time. Dynamic arrays have a protocol similar to that of standard arrays, except that we use method calls rather than subscript syntax. We must be able to insert and retrieve data at arbitrary index positions.
INTERFACE DynamicArray;
IMPORT Object, Collection;
TYPE
T <: Public;
Public = Collection.T OBJECT
METHODS
atPut(where: CARDINAL; what: REFANY);
(* Put what at location where. *)
at(where: CARDINAL):REFANY;
(* Return the value at location where. *)
extend(by: CARDINAL);
(* Extend the length of the array by appending "by" new cells. *)
physicalSize():CARDINAL;
(* Return the current physical size of the array. *)
swap(a,b:CARDINAL);
(* Swap the values at locations a and b. *)
sequentialSearch(what: REFANY; VAR where: CARDINAL):BOOLEAN;
(* Search for what. Return TRUE if found and set where to the cell number.
If not found, return false and do not change where. *)
END;
PROCEDURE New(size: CARDINAL): T;
(* Set the initial length to size. *)
TYPE
Iterator <: Collection.Iterator;
END DynamicArray.
The key methods in DynamicArray.T are at and atPut, which both take integer arguments. This argument is the ordinal position in the large array that we wish to reference. We don't need a position class for these because a position is just the integer index of a data item. We, of course, need an iterator class for these, as we do for all collections. The extend metod can be use to extend the length of a dynamic array by the amount of its by parameter.
An interval is a finite algebraic sequence of integers, like 1,4,7, 10. This interval goes from 1 to 10 by 3. Intervals are useful in array processing when we want to process some but not all elements in the array. They are equally useful in similar situations that do not involve arrays. An interval is a fixed sized collection, that may not be added to or removed from once it is created. An iterator over the interval will yield us the elements in the sequence in order. The protocol is:
INTERFACE Intervals;
IMPORT Object, Collection;
TYPE
T <: Public;
Public = Collection.T OBJECT
METHODS
at(loc: INTEGER):INTEGER;
(* Return the integer at position loc. *)
size(): CARDINAL;
(* Return the number of integers in the interval. *)
END;
PROCEDURE New(fromVal, toVal, byVal: INTEGER): T;
TYPE
Iterator <: Collection.Iterator; (* returns elements in Integers.T *)
END Intervals.
The iterator is completely standard. It yields the next item as an Integer.T. The interval method at gives us the value at a relative position. For example in 1,4,7,10, the 7 is at position 2 (assuming we start counting with zero). size gives us the number of elements in the collection. For the above example it should be four.
The previous sections briefly described a number of classes and their protocols. This particular set of classes was chosen both to illustrate data structuring techniques and, more importantly, because they have been shown to be useful in a wide variety of programming situations. If object oriented programming is to meet its promise it should be possible to use this class library without examining the implementations of most of the methods. It should also be possible to leverage off of the above classes using inheritance to extend the capabilities of the classes. For example, in our discussion of binary trees we did not show a method to put new data into the left child of the current position. If such a method were needed it could be added by modification of the existing class BinaryTree.Position, or by creation of a new class that inherits from this one and provides the new functionality. Ideally, if the base class hierarchy is sound, is should not be necessary to modify it. It should also not be necessary to frequently override methods to correct behavior. Overriding should be used to extend the class to new capabilities and when new instance variables need to be properly handled in a subclass.
This is the basic idea of abstraction at this level. Create a collection of ideas (stack, queue, largeInteger...). Construct classes to implement the ideas and implement the ideas consistently and faithfully. Understand the classes by reference to the ideas, not by reference to the code, which contains too many details for us to effectively remember. Build complex ideas on the backs of simpler ideas. Use inheritance to implement the complex ideas using previously implemented classes. Proceed primarily from the general to the specific as you design and build.
This chapter has given the interfaces of the main subclasses of Maginitude and Collection as well as classes associated with collections. It also gives the ideas underlying each class. These classes form a tree, in which a lower element in the graph inherits protocol and some functionality from those above it. We thus obtain a high degree of reusability in the system, with many components of the ancestor classes being reused in the descendant classes.
Figure 4.7 summarizes the relationships between most of the classes discussed in the book. It contains a number of classes here that are not discussed in this chapter, which has focused on only the main classes.
1. (4.2.7) Give an interface file for class Complex.T.
2. (4.2.8) In the last chapter you were asked to implement methods such as lessEqual and greater from the class Magnitude.T. If you implement Integers.T and build appropriate less and equal methods, will your inherited lessEqual and greater work in Integers.T? Keep in mind that Magnitude.T implemented some methods as errors. Keep the dynamic binding principle in mind.
3. (4.2.9) Give a interface file for class Real.T.
4. (4.2.9) Give the protocol for Real.T and Complex.T;
5. (4.3.5) Give a critique of the design and implementation of the real stack class discussed in Chapter 2 and implemented in the exercises. In what ways (if any) is the finite stack class discussed in Chapter 3 an improvement on it? In what ways is the stack class discussed in this chapter an improvement on both of those? Is there a tradeoff? That is to say, have we given up anything to gain the advantages you cite?
6.
7. (4.3.10) We could easily add the two key methods of our Dynamic Array class to the List class:
atPut(i: INTEGER; o: Object.T);
at(i: INTEGER):Object.T;
8. (4.4) Consider the classes in Figure 4.7. Are there any that you would like to include? Try to think of one or two additional classes that might be developed as subclasses of Magnitude.T or Collection.T. Design protocols for your classes. How would they be used. What do your methods do. Give pre-conditions and post-conditions where appropriate. Are there other major classifications (such as magnitude or collection) that have been omitted?
9. (4.4) Re-evaluate your answer to Exercise 8 of the last chapter.