Lend me an arm; the rest have worn me out
With several applications:
Shakespeare, All's Well That Ends Well
Now it is time to deliver on the promise. We have seen a lot of protocol and the implied promise that it would be useful. We shall now show two applications that build on the above framework and do some things that every student of computer science should see. Our methodology will be to create a new class to form the framework for the solution of our problem. In each case the instance variables of the new class will have types that come from the hierarchy discussion in Chapter 4. We shall use these instance variables directly, without needing to rebuild the classes from which they come. The new, application level, class can be thought of as a "director" that gets the messages sent to the instance variables at the right time. In a certain sense we will be writing "high level" application oriented code in the methods of these new classes, drawing on the "low level" classes from the hierarchy.
The first application will be a simulator for deterministic finite automata. The DFA is an abstract computing machine, simpler than a computer, but capable of carrying out some simple computation tasks. We shall use Dictionaries to help us, as well as TEXTs, and Characters.
The other application involves the translation of arithmetic expressions from the standard "infix" form that people are used to, into a "postfix" terminology that is very suitable for computers. The technique is called operator precedence translation, and it is a very important compiler technique. The fundamental data structure here is the stack, though we shall also use TEXTs and Integers. A variation will use a form of BinaryTree.
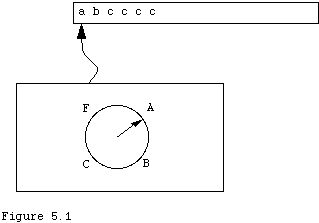
A finite automaton is a simple model of computation that is sufficient for some tasks but inadequate for others. Finite automata also have great theoretical importance due to their equivalence to a class of languages called regular languages. Simply, a DFA is a machine that has input, but no output. It has a fixed number of internal states, and at any given time it is "in" one of these states. It runs a fixed program and when it reaches the end of its input it announces whether the input was OK or bad, depending on what its internal state is at the time. A program is just a table of the transitions it should make from state to state. A schematic of a DFA is shown in Figure 5.1
One of the states is the start state, and one or more are final states. If the machine reaches the end of the input and is in a final state the input was OK, otherwise it was bad. The operation of the machine is as follows. The (finite) input is written on a tape and the machine is set with its read mechanism over the leftmost symbol on the tape. Symbols on the tape come from some fixed finite alphabet. The state of the machine is its initial state. When started the machine reads the current input symbol and moves the read mechanism one symbol to the right. Then, depending on the current state and the symbol just read, the machine changes its state according to its program. When the end of the tape is reached, the machine says OK or "accepts its input" if it is in a final state, otherwise it rejects the input. If the machine is in some state and its program has no instruction corresponding to the current symbol the machine also halts in error and rejects the input.

Deterministic Finite Automaton.i.Deterministic finite automaton; A DFA consists of five parts: 1. a finite tape alphabet. 2. a finite set of states..i.State of a DFA; 3. a specification of the start state.i.Start state of a DFA;. 4. a specification of the final states. .i.Final states of a DFA; 5. a program which consists of a finite set of triples (s, r, t) where s is the current state, r is the read symbol and t is the state that the machine should "move" to in case we are in state s while reading r. |
A DFA program is a partial function whose domain is the Cartesian product of the states and the alphabet, and whose range is the set of states. We can model a DFA by modeling its program function. A tabular presentation of the function is adequate for some purposes. The following example of a DFA has four states A,B,C,F, and an alphabet of three letters a, b, and c. This DFA has initial state A, and only a single final state, F and its transition function is:
(A,a) -> B
(A,b) -> C
(B,b) -> F
(C,a) -> F
(F,c) -> F
Another simple way to model a DFA is with a directed graph, with one node for each internal state. The arcs in the graph model the various triples (s, r, t) in the program. We simply draw an arc from s to t and label it with r. Final states are drawn as double circles, and the initial state is marked with an "in" arc from no node. The above DFA is shown in Figure 5.2.
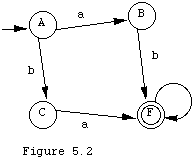
This DFA has four states, A,B,C, and F. The initial state is A and its only final state is F. It will accept any string that consists of an "a" followed by a "b" followed by zero or more "c"s. It will also accept strings consisting of "ba" followed by zero or more "c"s. All other strings will be rejected. A set of strings is called a language, and a language for which there is a DFA accepting exactly the strings in that language is called a regular language. Regular languages have both theoretical and practical value. Their practical importance comes from the fact that the words and symbols that we use to express the programs in most programming languages form a regular language. Thus, in Pascal, these basic symbols, such as the key word "RECORD" and the identifier VAT37, as well as the special symbols such as <= and := form a regular language. Individually these symbols are called tokens. The scanner within a compiler has the job of translating the stream of characters in the program text file into a stream of tokens to make the rest of the job of translating easier. Scanners are often nothing more than a simulator of some DFA equivalent to the "token language". In this section we want to develop a simulator for DFAs. We shall do it in a general way, permitting a user to construct a DFA and then give it an input to determine if that DFA accepts that input string.
Scanning Problem Separate the characters of a file into meaningful words and symbols called tokens. If the words and symbols form a regular language then a DFA may be used to solve the scanning problem. |
We take our own advice above and model the DFA as a graph. Now we need to figure out how to model the graph. Let us model the nodes directly, and create a new class DFANode.T. This new class will actually do little more than package up functionality provided by our other classes. Other than an initializer it will only need two methods to do the work of a DFA. A DFA will be some collection of these nodes. We could create some class to handle this collection, or we could use some existing class like Set.T, but there is an even easier way. If each node simply knows who its neighbors are in the graph then the graph as a whole is modeled in a "distributed" way, as there is no central collection of information about the graph.
Another way to think of this is to take its transition function and partition it into a collection of functions by projection onto each state. In other words we put two transitions into the same function in the partition if they map the same state. This way we get a function for each state rather than one function for the whole DFA. What we shall do is to model this set of functions to model the DFA. For the DFA discussed above we get four partial functions, one for each state. We first just select all mapping pairs that "start" at the same state.
State A:
(A,a) -> B
(A,b) -> C
State B:
(B,b) -> F
State C:
(C,a) -> F
State F:
(F,c) -> F
Then we just project these onto the states to get the required functions.
State A:
a -> B
b -> C
State B:
b -> F
State C:
a -> F
State F:
c -> F
When we initialize a node we should indicate whether it will be a final state or not. We also need a way to store the information about the neighbors and the labels on the arcs to those neighbors. A dictionary is especially suited for this as a dictionary represents a function and so does the DFA program. A dictionary is a set of association pairs, with the key in the association being a magnitude and no key appearing twice in the dictionary. We can build associations in this case by using the characters in the input alphabet as the keys. (This is a restriction. The definition of a DFA permits more general sets of symbols.) The value in the association will be the state at the other end of the arc. Note that only the state at the "tail" of an arc needs to store the arc.
Finally we need to determine how the tape will be represented and how we shall simulate the reading of the tape by the DFA as a whole. The answer to the former question is simply to use the built-in TEXT type of Modula-3 as these are finite sequences of characters as our tape is. Reading the tape can be accomplished by simply sending the original string to some state (the initial state) as a parameter to the run message. The state node removes the first character from the string, looks it up in its own dictionary and if it gets a match it puts the DFA into the corresponding state by sending the string (with its first character removed) to that state as a parameter to another run message. If a state doesn't have an association for a given input character it halts the run with an error message but doesn't pass on the run message. Also, if a state is sent an empty string it announces "accept" if it is a final state but "reject" otherwise.
Required Classes TEXT Object.T DFANode.T Magnitude.T Association.T Character.T Collection.T Lists.T Set.T Dictionary.T |
The public interface (we haven't defined a private interface here) for our class follows.
INTERFACE DFANode;
IMPORT Object, Character, Dictionary, Wr;
TYPE
T = Object.T OBJECT
fIsFinal: BOOLEAN;
fNeighbors: Dictionary.T;
METHODS
initDFANode(final: BOOLEAN): T := InitDFANode;
addNeighbor(n: T; ch: Character.T) := AddNeighbor;
run(input: TEXT) := Run;
OVERRIDES
clone := CloneDFANode;
writeIt := WriteDFANode;
copyFields := CopyDFANodeFields;
END;
PROCEDURE InitDFANode(self: T; final: BOOLEAN): T ;
PROCEDURE AddNeighbor(self: T; n: T; ch: Character.T) ;
PROCEDURE Run(self: T; input: TEXT) ;
PROCEDURE WriteDFANode(self: T; f: Wr.T) ;
PROCEDURE CloneDFANode(self: T): Object.T ;
PROCEDURE CopyDFANodeFields(self: T; o: Object.T);
PROCEDURE New(final: BOOLEAN): T;
END DFANode.
Generation of new nodes is standard:
PROCEDURE NewDFANode(final: BOOLEAN): T =
VAR result: T;
BEGIN
result := NEW(T);
Object.FailNil(result);
EVAL result.initDFANode(final);
RETURN result;
END NewDFANode;
PROCEDURE InitDFANode(self: T; final: BOOLEAN): T =
BEGIN
self.fIsFinal := final;
self.fNeighbors := Dictionary.New();
RETURN self;
END InitDFANode;
PROCEDURE AddNeighbor(self: T; n: T; ch: Character.T) =
BEGIN
self.fNeighbors.atPut(ch,n);
END AddNeighbor;
It is the run method that does all of the work. It assumes that the nodes have been created and initialized, and that each node has been given its complete list of neighbors. Run is sent to some state, with a parameter that is a TEXT.
PROCEDURE Run(self: T; input: TEXT) =
VAR
ch: Character.T;
n: T;
len: CARDINAL;
BEGIN
len := Text.Length(input);
IF len = 0 THEN
IF self.fIsFinal THEN
Wr.PutText(Stdio.stdout, "Accepted.");
ELSE
Wr.PutText(Stdio.stdout, "Rejected.");
END;
ELSE
ch := Character.AsCharacter(Text.GetChar(input,0));
n := self.fNeighbors.at(ch);
IF n = NIL THEN
Wr.PutText(Stdio.stdout, "Rejected--blocked.");
ELSE
n.run(Text.Sub(input, 1, len - 1));
END;
END;
END Run;
We begin by checking to see if the string is empty and if so make the proper announcement. Otherwise we extract the first character from the string and use the method at from our dictionary class to see if there is a corresponding association in fNeighbors. If so, at will return the value in the association rather than the association itself. If we get a non-NIL value then it represents the next state so we remove the first character from the string and pass the run message on to the new state.
To create the DFA given in the example above and test it on the tape "abccccc" we would use the following code. The result should be "Accepted".
MODULE Main;
IMPORT DFANode, Character;
VAR A,B,C,F : DFANode.T;
BEGIN
A := DFANode.New(false);
B := DFANode.New(false);
C := DFANode.New(false);
F := DFANode.New(true);
A.addNeighbor(B, Character.AsCharacter(`a'));
A.addNeighbor(C, Character.AsCharacter(`b'));
B.addNeighbor(F, Character.AsCharacter(`b'));
C.addNeighbor(F, Character.AsCharacter(`a'));
F.addNeighbor(F, Character.AsCharacter(`c'));
A.run("abccccc");
END Main.
The corresponding m3makefile would be
implementation ("Main")
module ("Object")
module ("Magnitude")
module ("Collection")
interface ("PRCollection")
module ("Lists")
interface ("PRLists")
module ("Character")
interface ("PRCharacter")
module ("Association")
interface ("PRAssociation")
module ("Set")
interface ("PRSet")
module ("Dictionary")
interface ("PRDictionary")
module ("DFANode")
import ("libm3")
program ("dfa")
Extensions
There are many variations on DFAs. A finite state transducer is simple to implement. This is like a DFA except that it produces some output when it makes a state transition. A program consists of quadruples (s, r, t, o) where o is produced when we move to state t if we are in state s and read symbol r. The modification to the above would be to store keys in our dictionary just as before, but construct pairs for the values. The pairs could consist of the output symbols and the transition states. Then Dictionary.T's at method would return one of these pairs and we could extract the information from it. Alternatively we could do the same thing by creating a new class to hold the pair of items and use these for the values. We would need a new addNeighbors routine and would need to override run to accomplish this.
Another, more complex variation is a Turing Machine, named for Alan Turing, one of the pioneers of computation theory. A Turing Machine can both read and write its tape, and it can move its tape head in either direction. Thus it can use the tape as a sort of changeable memory. It turns out that a Turing Machine is exactly equivalent to what we think of as a computer. There is a conjecture called "Church's Thesis" that anything that can be computed can be computed with a Turing Machine. Thus a Turing machine is the "most powerful" sort of abstract machine. Not powerful in the sense of fast or easy to use, but powerful in the sense of being able to compute the most things.
An intermediate machine is called a Push Down Automaton. In such a machine there is a single stack onto which we may push symbols or pop them. Transitions now depend on the current state, the symbol at the read mechanism of the tape, and the symbol on top of the stack. The machine does a transition from some state s by reading the next input symbol r, popping the top of the stack p, and, if there is a transition from the current state for this combination of input symbol and the stack top, moving to a new state and pushing some symbols (several perhaps) onto the stack. Termination also generally requires that the stack be left empty. We could build this by treating the stack in the same way that we treated the tape in a DFA: just pass it on to the next state. Another way is to create a separate class for the PDA as a whole and let it store the stack. A PDA.Node will then be told what PDA it is part of when it is initialized. It will store this as an instance variable. When it comes time to pop it just sends the pop message to that instance variable.
INTERFACE PDA;
IMPORT DFANode, Object, Character, Dictionary, Stack, Wr;
TYPE
Node = DFANode.T OBJECT
fPDA: Stack.T;
METHODS
initPDANode (aPDA: T) := InitPDANode;
transition(NBR: Node; pushing: TEXT; trans: CHAR; top: CHAR) := Transition;
OVERRIDES
run := Run;
writeIt := WriteIt;
END;
T = Object.T OBJECT
PDS: Stack.T;
initial: Node;
METHODS
initPDA() := InitPDA;
newNode(isInitial, isFinal:BOOLEAN):Node := NewPDANode;
run(aTape: TEXT) := RunPDA;
END;
PROCEDURE New():T;
(* Create a PDA object. Then create several Node objects, indicating exactly
one as initial and at least one as final.
Then set up the transitions among the nodes. Finaly Run the PDA on some tape. *)
PROCEDURE InitPDANode(self: Node; aPDA: T):Node;
PROCEDURE Run(self: Node; input: TEXT);
PROCEDURE Transition(self: Node; NBR: Node; pushing: TEXT; trans: CHAR; top: CHAR);
PROCEDURE WriteIt(self: Node; f: Wr.T);
PROCEDURE InitPDA(self: T);
PROCEDURE NewPDANode(self: T; isInitial, isFinal:BOOLEAN): Node;
PROCEDURE RunPDA(self: T; aTape: TEXT);
END PDA;
Here we do a bit more than in DFANode.T. We encapsulate the PDA as a whole in class PDA.T. The client will interact mostly with this class, first by creating one and then creating nodes in the class by sending the newNode message to the PDA object. The PDA itself creates the node, sending a reference to its own internal stack to the newly created node so that the node may push and pop this stack.
In PDA.Node a transition must somehow use both the trans and the top as the key and construct a value with the rest of the information. We can put trans and top into an IdentityAssociation.T for the key inserted into the dictionary. Identity associations are like associations except the equal method checks identity of keys and values. We also put the NBR and pushing into another IdentityAssociation.T for the value (pushing will need to be stored as a TEXT). Run will need to extract and decode this information from the dictionary. It will also have to push all of the characters of the push string onto the stack. We show run below. The rest is an exercise. Note that an "empty" stack is one with just the `$' character, which is initially pushed. Note also that a pop is always done, so that if `$' is ever popped it must be pushed. Notice that our dictionary will have "pairs" of "pairs" for its contents: the key of each member is an IdentyAssociation, and so is the value.
PROCEDURE Run(self: Node; input: TEXT) =
VAR aChar, topChar: Character.T;
aTrans: Node;
key, value: IdentityAssociation.T;
pushString: TEXT;
aValue: REFANY;
BEGIN
IF input.empty() THEN
TRY
IF self.fIsFinal AND self.fPDA.top() = Character.asCharacter('$') THEN
Wr.PutText(Stdio.stdout, "Accepted.");
ELSE
Wr.PutText(Stdio.stdout, "Not accepted.");
END;
EXCEPT
| Thread.Alerted =>
| Wr.Failure =>
END;
ELSIF self.fPDA.empty() THEN
TRY
Wr.PutText(Stdio.stdout, "Not accepted--underflow in stack.");
EXCEPT
| Thread.Alerted =>
| Wr.Failure =>
END;
ELSE
aChar := Character.AsCharacter(Text.GetChar(input,0)); (* get first element of tape *)
key := IdentityAssociation.New(aChar, self.fPDA.top());
value := self.fNeighbors.at(key);
IF value # NIL THEN
pushString := value.getKey();
self.fPDA.removeFirst();
FOR i := 0 TO Text.Length(pushString) - 1 DO
self.fPDA.push(Character.asCharacter(Text.getChar(pushString, i)));
END;
aTrans := value.getValue();
aTrans.run(Text.Sub(input, 1, len - 1));
ELSE
TRY
Wr.PutText(Stdio.stdout, "Not accepted--halted.");
EXCEPT
| Thread.Alerted =>
| Wr.Failure =>
END;
END:
END;
END;
In the final section we show how to translate ordinary arithmetic expressions, which may or may not involve parentheses into postfix form, which is useful for computation. In fact the Hewlett- Packard company has built a very successful line of calculators around the idea of postfix expressions. In this section we shall use stacks, dictionaries, strings, characters, and integers.
Standard form for arithmetic expressions in called infix: the operator is in between its operands as in A + B. In postfix form the operator comes after all of its operands as in A B +. There are a number of advantages of postfix. The most important is that parentheses are not necessary, unlike infix form. For example with infix form the expression A + B * C is ambiguous except for a special rule that informs us that the multiplication is to be done first, which means that the form is treated as if it were equivalent to A + (B * C) rather than as (A + B) * C. If we should happen to mean the latter form, we need to use the parentheses. In postfix notation A + (B * C) would be written as A B C * + and (A + B) * C would be A B + C * removing any ambiguity and not needing parentheses. Postfix expressions can also be easily evaluated while reading the expression left to right if there is a stack available to hold intermediate results. The rule is simply: if you have an operand then push it. If you have an operation then pop the correct number of operands for that operation and apply it. Then push the result. For the expression 3 4 + 5 *, we would first push 3 then 4. We then see the + so we pop the 4 and 3, add them and push the resulting 7. The next symbol is 5 so we push it and the last is * so we pop 5 then 7, multiply them and push 35. This is the end of the input so the result is at the top of the stack: 35.
A translator must do several things. First, it must solve the scanning problem if the input is a character stream. Secondly it must solve the parsing problem. That is to say, it must determine if its input can be formed into a correct token stream. It must verify that the sequence of the tokens is valid. For many languages this is accomplished using a push down automaton. We will use something similar here. An example of an incorrect token string is an unclosed parenthesis. Finally the translator must produce some correct output: the translation. Here we will just output a postfix string which is equivalent to the input string assuming that the input was correctly formed.
The Parsing Problem Determining if the tokens of a language form a correct sequence. If the language is "Context Free," then a push down automaton may be used to solve the parsing problem. (Ch. 13) |
Here we want to write a program to translate infix expressions into an equivalent postfix form. The inspiration for this section came from a book Computing Problems for FORTRAN Solution, Robert Teague, Canfield Press, 1972. It is a book worth having even if you never program in FORTRAN. The translation technique is called Operator Precedence Translation. It is a technique that has been in use for a long time, and is still used in many C compilers. The basic idea is to assign numeric values to each kind of symbol. These precedences determine how a symbol will be handled. A stack is also used to hold symbols that have been seen in the input but have not yet been transferred to the output. There are separate precedences for symbols in the stack and in the input. Suggested values are:
Char input stack use
; 0 0 mark end of input
= 1 1 assignment operator
) 2 0
+,- 3 4
*,/ 5 6
letter 7 8
digit 7 8
( 9 2
A = (B + C) * (D + E) ;
into
A B C + D E + * =
The protocol of our system is shown below. We create a scalar type for the various token types and a class to manage the translation. The class will maintain its own stack and its own input string as instance variables.
Required Classes TEXT Object.T Infix.T Collection.T Lists.T Stack.T Set.T Dictionary.T BinaryTree.T Magnitude.T Character.T Integers.T Association.T |
The public interface to our new class is Infix.
INTERFACE Infix;
IMPORT Object, Text, BinaryTree;
TYPE
T <: Public;
Public = Object.T OBJECT
METHODS
translate(t: TEXT):TEXT; (* infix -> postfix *)
END;
PROCEDURE New():T;
END Infix.
The private interface shows details as usual. The comparison between the two interfaces gives a good idea of how much detail can be hidden.
INTERFACE PRInfix;
IMPORT Object, Infix, Text, BinaryTree, PRBinaryTree, Stack, Dictionary, Wr;
TYPE
TokenType = {lparen, rparen, ident, digit, addop, mulop,
pwrop, assign, endmark};
Token = Object.T OBJECT
fToken: TokenType;
fCharValue: CHAR;
fOperator: BOOLEAN := FALSE;
END;
REVEAL
Infix.T = Infix.Public BRANDED OBJECT
iValues, sValues: Dictionary.T;
fInfix, fPostFix: TEXT := NIL;
fCurrentValue: TEXT := NIL;
METHODS
initInfix(): Infix.T := InitInfix;
getToken():Token := GetToken;
lookupTop(t: TokenType):INTEGER := LookupTop;
lookupInput(t: TokenType): INTEGER := LookupInput;
OVERRIDES
translate := Translate;
clone := CloneInfix;
writeIt := WriteInfix;
copyFields := CopyInfixFields;
END;
PROCEDURE InitInfix(self: Infix.T): Infix.T ;
PROCEDURE GetToken(self: Infix.T):Token;
PROCEDURE LookupTop(self: Infix.T; t: TokenType):INTEGER;
PROCEDURE LookupInput(self: Infix.T; t: TokenType): INTEGER;
PROCEDURE Translate(self: Infix.T; t: TEXT):TEXT; (* infix -> postfix *)
PROCEDURE WriteInfix(self: Infix.T; f: Wr.T) ;
PROCEDURE CloneInfix(self: Infix.T): Object.T ;
PROCEDURE CopyInfixFields(self: Infix.T; o: Object.T) ;
END PRInfix.
Once we have built the above class we may use it as in the following main program. Variables x and y have type TEXT, and translator has type Infix.T.
MODULE Main;
IMPORT Wr, Stdio, Infix;
VAR translator: Infix.T;
x,y: TEXT;
BEGIN
Wr.PutText(Stdio.stdout,"Operator Precedence Translation");
translator := Infix.New();
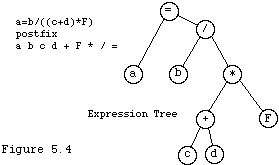
x := "a=b/(c+d)*F";
Wr.PutText(Stdio.stdout,"postfix");
y := translator .translate(x);
Wr.PutText(Stdio.stdout, y);
END Main;
The output from this is
Operator Precedence Translation
postfix
a b c d + / F * =
implementation (Main)
module (Object)
module (Magnitude)
module (Collection)
interface (PRCollection)
module (Lists)
interface (PRLists)
module (Integers)
interface (PRIntegers)
module (Character)
interface (PRCharacter)
module (Association)
interface (PRAssociation)
module (Set)
interface (PRSet)
module (Dictionary)
interface (PRDictionary)
module (Stack)
interface (PRStack)
module (BinaryTree)
interface (PRBinaryTree)
module (Infix)
interface (PRInfix)
import (libm3)
program (infix)
The translation proceeds by reading the inputs from left to right. When we need a new input symbol we call getToken and it returns an object to us corresponding to the next significant symbol in the input. We maintain a stack. The rules for its use are:
Operator Precedence Translation 1. If the next input token has precedence greater than the precedence of the stack top token then push the input (removing it from the input by calling getToken). 2. If the input precedence is the same as the stack precedence then discard the input and pop the stack, discarding the top value as well. 3. If the input precedence is less than the stack precedence then pop the stack top and append the result to the output, but leave the input as it is. [Floyd, 1963] |
This simple rule forms the basis of our translation routine. However we also need to represent our tokens, store the precedences, and manage the stack. For tokens we want objects so that we can push them onto stacks, but otherwise they are just like records. We won't even give them any methods. Stacks come for free as we may just use Stack.T without change.
Token = Object.T OBJECT
fToken: TokenType;
fCharValue: CHAR;
fOperator: BOOLEAN := FALSE;
END;
typedef SToken *PToken;
The precedences may be held in two dictionaries; ivalues for the input precedences and svalues for the stack precedence values. These are best saved as instance variables of an op translator. They are created and filled with their lookup tables when the translator is constructed. The constructor must also create a stack to hold the intermediate information.
PROCEDURE InitInfix(self: T): T =
BEGIN
self.iValues := Dictionary.New();
self.sValues := Dictionary.New();
self.iValues.atPut(AsInteger(ORD(TokenType .endmark)), AsInteger(0));
self.iValues.atPut(AsInteger(ORD(TokenType .assign)), AsInteger(1));
self.iValues.atPut(AsInteger(ORD(TokenType .rparen)), AsInteger(2));
self.iValues.atPut(AsInteger(ORD(TokenType .addop)), AsInteger(3));
self.iValues.atPut(AsInteger(ORD(TokenType .mulop)), AsInteger(5));
self.iValues.atPut(AsInteger(ORD(TokenType .ident)), AsInteger(7));
self.iValues.atPut(AsInteger(ORD(TokenType .digit)), AsInteger(7));
self.iValues.atPut(AsInteger(ORD(TokenType .lparen)), AsInteger(9));
self.sValues.atPut(AsInteger(ORD(TokenType .endmark)), AsInteger(0));
self.sValues.atPut(AsInteger(ORD(TokenType .assign)), AsInteger(1));
self.sValues.atPut(AsInteger(ORD(TokenType .rparen)), AsInteger(0));
self.sValues.atPut(AsInteger(ORD(TokenType .addop)), AsInteger(4));
self.sValues.atPut(AsInteger(ORD(TokenType .mulop)), AsInteger(6));
self.sValues.atPut(AsInteger(ORD(TokenType .ident)), AsInteger(8));
self.sValues.atPut(AsInteger(ORD(TokenType .digit)), AsInteger(8));
self.sValues.atPut(AsInteger(ORD(TokenType .lparen)), AsInteger(2));
RETURN self;
END InitInfix;
 This
procedure just models the DFA directly. It's case statement is the means of
determining a state transition.
This
procedure just models the DFA directly. It's case statement is the means of
determining a state transition.
PROCEDURE GetToken(self: T):Token =
VAR result: Token;
tok: TokenType;
chVal: CHAR;
isOperator: BOOLEAN := FALSE;
BEGIN
result := NEW (Token);
Object.FailNil(result);
IF NOT Text.Empty(self.fCurrentValue) THEN
WHILE NOT Text.Empty(self.fCurrentValue) AND
(Text.GetChar(self.fCurrentValue,0) = (' ')) DO
self.fCurrentValue := Text.Sub(self.fCurrentValue, 1, Text.Length(self.fCurrentValue)-1);
END;
chVal := Text.GetChar(self.fCurrentValue,0);
isOperator := FALSE;
self.fCurrentValue := Text.Sub(self.fCurrentValue, 1, Text.Length(self.fCurrentValue)-1);
CASE chVal OF
| '(' => tok := TokenType.lparen;
| ')' => tok := TokenType.rparen;
| '0'..'9' => tok := TokenType.digit;
| 'a'..'z' => tok := TokenType.ident;
chVal := VAL(ORD(chVal)-ORD('a')+ORD('A'),CHAR);
| 'A'..'Z' => tok := TokenType.ident;
| '+','-' => tok := TokenType.addop; isOperator := TRUE;
| '*','/' => tok := TokenType.mulop; isOperator := TRUE;
| '=' => tok := TokenType.assign; isOperator := TRUE;
| ';' => tok := TokenType.endmark;
ELSE Object.Error( "Infix.GetToken: not defined.");
END;
ELSE
tok := TokenType.endmark;
chVal := ';';
END;
result.fToken := tok;
result.fCharValue := chVal;
result.fOperator := isOperator;
RETURN result;
END GetToken;
This routine is just a string processor, getting characters from the input and comparing them against various possibilities. At the end it returns the desired information.
The translate method is the main engine of the class, of course, but it needs two additional functions to gain easy access to the precedence values that we stored in the dictionaries in the constructor. These two functions, lookupTop and lookupInput, search the respective stack and input dictionaries for the precedences of the current stack top and input token respectively. The key searching is handled by a simple call to at from the dictionary class.
PROCEDURE LookupTop(self: T; t: TokenType):INTEGER =
BEGIN
RETURN NARROW(self.sValues.at(AsInteger(ORD(t))), Integers.T).value();
END LookupTop;
PROCEDURE LookupInput(self: T; t: TokenType): INTEGER =
BEGIN
RETURN NARROW(self.iValues.at(AsInteger(ORD(t))), Integers.T).value();
END LookupInput;
The translation routine simply compares the top of the stack with the next input token. At any time that a new token is needed we just call getToken. Whenever we are done with the top of the stack we may pop.
The initialization guarantees that the stack is in a known state before we start. We push a special marker onto it. We also append the semicolon character to the input to be certain that we will recognize its end.
PROCEDURE Translate(self: T; t: TEXT):TEXT = (* infix -> postfix *)
VAR result, currentValue: TEXT;
aToken, stacktop, marker: Token;
topVal, inputVal: INTEGER;
transError: BOOLEAN;
expressionStack: Stack.T;
BEGIN
marker := NEW( Token);
Object.FailNil(marker);
marker.fToken := TokenType.endmark;
marker.fCharValue := ';';
expressionStack := Stack.New();
expressionStack.push(marker);
transError := FALSE;
self.fCurrentValue := t;
self.fInfix := t;
self.fTree := NIL;
result := Text.FromChar(' ');
aToken := self.getToken();
WHILE (aToken.fToken # TokenType.endmark) AND NOT transError DO
IF expressionStack.empty() THEN transError := TRUE; END;
stacktop := expressionStack.top();
topVal := self.lookupTop(stacktop.fToken);
inputVal := self.lookupInput(aToken.fToken);
IF topVal > inputVal THEN (* append to output *)
stacktop := expressionStack.pop();
result := Text.Cat(result, Text.FromChar(stacktop.fCharValue));
result := Text.Cat(result, Text.FromChar(' '));
ELSIF topVal < inputVal THEN (* push the input token *)
expressionStack.push(aToken);
aToken := self.getToken();
ELSE (* equal -- discard both *)
EVAL(expressionStack.pop());
aToken := self.getToken();
END;
END;
WHILE NOT expressionStack.empty() DO
aToken := expressionStack.pop();
IF aToken.fToken # TokenType.endmark THEN
result := Text.Cat(result, Text.FromChar(aToken.fCharValue));
result := Text.Cat(result, Text.FromChar(' '));
END;
END;
self.fPostFix := result;
RETURN result;
END Translate;
The main part of the translate method compares the precedence, topVal, of the top of the stack, to the precedence, inputVal, of the current input. If topVal is greater then we pop the stack and append the result to the output theResult. If topVal is less than inputVal we push the input token. Finally, if they are equal we discard both by popping and by calling getToken. When the input string has been completely processed we append any remaining contents of the stack to the output.
This class may be extended quite easily to permit the creation of an expression tree representing the expression as the translation proceeds. An expression tree will be a specialization of BinaryTree.T that we have seen.
Expression Tree A tree with the property that interior nodes represent operations. The children of a node represent operands of the operation at that node. Composite operands are represented by sub -trees. Elementary operands are represented by values. |
A new method, createExpressionTree in class Infix.T will create such a tree while translating. The logic of createExpressionTree is the same as that of translate except for the handling of the output. Instead of just appending an item to the output when the stack precedence is greater, we create a new tree node to hold the item just popped. In addition, if the item popped is an operator, like "+" we pop the appropriate number of operands for that operator from the stack (they will be at the top), attach them as children to the tree node just created, and finally push the tree node back into the stack. The details are left as an exercise.
Another extension that may be readily done is to turn the translator into an evaluator. The idea here is to evaluate expressions on the fly rather than to just transform the output. Suppose that our input consists of infix expressions with single digit (numeric) operands rather than symbolic names. Then in the translate method, instead of simply outputting symbols to the output string we may do the following. If the symbol to be output is an operand then push it, as an Integers.T, onto another stack, the evaluation stack. If the symbol is an operator then pop the correct number of operands for the operator off the evaluation stack and apply the operator to them using methods of Integers.T. The one further down in the stack is the leftmost operand. The result of applying the operation should be pushed back onto the evaluation stack. When the input is exhausted the result of the expression should be at the top of the evaluation stack.
It is possible to use the functionality of a class without understanding its implementation. All that is necessary is to understand its protocol, which consists of its interface and the specifications of the procedures defined by the interface.
The method of solving problems with such a class library is to create a new class (or a small collection of classes) that will orchestrate the usage of the functionality of a class hierarchy. This new class behaves much like the director of an orchestra who does not make music so much as helping the individual musicians coordinate their efforts toward a common end.
Our DFA class solved the problem of simulating the actions of a deterministic finite automaton using the existing functionality of dictionaries, associations, and strings, adding only the specific code necessary to the DFA itself. The Infix class used dictionaries and stacks, primarily, to translate infix expressions into postfix form.
1. (5.1) Complete the implementation of the PDA and test it. The following test code may be used for a partial test. Note that a transition on `$' at top of stack must see to replacing the `$' which gets popped to check it. The `$' is actually a bottom of stack indicator.
aPDA := PDA.New();
sA := aPDA .newNode(TRUE,TRUE);
sB := aPDA .newNode(FALSE,FALSE);
sA.transition(sB, "$a", 'a', '$');
sB.transition(sA, "", 'a', 'a');
sB.transition(sA, "$", 'a', '$');
aPDA.run( "aaaaa");
2. (5.1) A better implementation of push-down automata uses a list in a PDA object that holds references to all the states making up the PDA. One creates states using a message passed to a PDA, which creates the required state, inserts it into its list and, perhaps, returns a reference to it. Discuss the desirability of this. Implement it.
3. (5.2) Provide better error correction in the translator of section 5.2. Unless we modify the translator as suggested in Exercise 4 we will get garbage if we try to translate the string "A=MM" but we don't get an error message. We should either quit processing when we have seen a complete expression, with the next character not legal, or we should complain about the violation.
4. (5.2) Modify the translator of section 5.2 to accept long names for identifiers. Names should be permitted to be of type TEXT. This requires that we extend getToken and also modify the token class.
5. (5.2) Modify the translator of section 5.2 by adding an evaluator of infix expressions which consist of integer constant operands and the operations currently implemented.
6. (5.2) Modify the translator of section 5.2 by adding an evaluator of infix expressions which consist of any constants or identifiers and operations. Implement storage for the identifiers as a dictionary of name-value associations. When a name is given a value enter the name value association into the dictionary. When a name is used, retrieve the association corresponding to the name to get access to the value.
7. (5.2) Modify the translator of section 5.2 by turning it into an infix to postfix fraction translator. Input of fractions should be in the same form that Fraction.T's writeIt method uses to output them. This will require modifying getToken so that it looks for the opening bracket symbol.
8. (5.2) Combine Exercises 5 and 7 above. Create a fraction calculator.
9. (5.2) Complete the implementation of Infix by providing for the creation of expression trees as suggested at the end of the section 5.2.
10. (5.2) Claim. The operation of Infix.T's translate method is just the operation of a particular PDA. Discuss the validity of this claim.
11. (5.2) This exercise is quite long, almost a project. Create a scanner for the Infix.T class using the ideas about DFA's in section 5.1. In particular:
1. We need to return a token from the DFA run method (rather than print a message) so that the caller will know which token was in the input. Method run needs to be a function returning a Token.
2. A scanner needs to be called several times to retrieve several tokens, not just one. The best way to do this is to consider the input string as a sequence of "tapes" rather than a single one, with each one terminated by the beginning of the next, rather than the end of the tape. This requires a change in the definition of acceptance. We scan until we have no possible transition from some state. If this state is a final state we consider we have accepted, if it is not final we have not accepted any token. If we halt and accept we should return the token whose fValue has been set so as to indicate what was seen in that part of the input: an element of TokenType. If we halt and reject we set fValue to be notoken.
3. Each call of run will consume only part of the input string so it should return the remaining portion so that the next call to run can resume.
4. When a state is constructed it should be told what value of TTokenType it should return if run halts in that state. Non final states must return notoken and others return a token indicating what has been seen in the input.
The following represent larger projects that may be undertaken, or at least begun, now. They may also be delayed until the implementations and further details of the classes in our hierarchy have been discussed in the following chapters. Expect to spend at least a few weeks in developing these programs. Some of them seem rather open-ended. This is intentional.
A relational database consists of a set of relations. A relation consists of a set of tuples over the same set of attributes . A tuple can be thought of as a dictionary in which the keys are exactly the set of attributes and the values are arbitrary values. Pictorially, you can think of a relation as a two dimensional table with the attributes labeling the columns and the tuples forming the rows. In the following example, taken from Chapter 15 of this book, the attributes are <Name>, <Address>, etc. and one tuples as a dictionary is { (<Name>, <Fein, Jacob>), (<Address>, <10 Oak>), ...}.
Name Address Home Phone Business Phone Fein, Jacob 10 Oak 555-1234 555-2234 Hai, Sari 3 First 555-4312 555-3312 Low, Judith 22 Elm 555-2314 555-3314 Ng, Lai 92 Third 555-2134 555-1134 Ng, Mary 92 Third 555-2134 555-4434 Smith, John 52 Maple 555-3214 555-2214
The natural join of two relations, A and B, is a third relation, J, such that:
1. The attribute set of J is the union of the attribute sets of A and B.
2. Let X represent the intersection of the attribute sets of A and B. If each of A and B have a tuple whose values on the attributes in X are identical, then J has a tuple formed by unioning the dictionaries of those tuples from A and B.
A consequence of rule 2 is that if the attribute sets of A and B are disjoint (the intersection is empty) then J consists of the Cartesian product of A and B: each tuple of A unioned with each tuple of B.
(a) Design an inventory system for a grocery warehouse. The inventory is a list of products. A product consists of the product description ("beans") and a list of items. An item consists of a supplier ("Shurfine") and a quantity on hand. You need to be able to create new products and new items, to adjust the quantities up and down as items are bought and sold, and to remove items when a supplier for an item is discontinued. Give thought as to what classes need to be designed, which classes the above suggested methods properly belong to, and how everything is to be implemented.
(b) Discuss your design with someone else. Modify it as necessary.
(c) Build the final design.
A maze can be built as a two dimensional array. Some of the cells of the array can be occupied by obstructions. The obstructions may be used to build walls and rooms. Some cell of the maze is marked as the goal, and the robot's aim will be to find (move to) the goal. It must be possible to create a new maze, place and remove obstructions, and inquire as to the presence of an obstruction in a particular cell. It will also be useful to be able to write a maze to a file and read it back in, since mazes are tedious to build. Note that all "cells" outside the maze boundary are treated as obstructed.
A robot occupies a cell of a maze, and when created is placed at some cell. It's purpose is to seek the goal cell in the maze by moving to it without passing through any obstructions. To do this the robot must be able to move from one cell to an adjacent cell to its north, east, south, or west. It may only move if the resulting cell does not contain an obstruction. To carry out its task, a robot needs some memory. One way to organize the memory is to keep a set of the cells that it has already visited, so that it doesn't wind up going around in circles, and also two stacks. The first stack contains those cells on a path taking the robot back to its starting point. This "current path" stack may be used in case the robot explores a dead end in the maze and needs to back out of it and resume at the most recent crossing point. The other stack is the "trials" stack and it contains hints about where the search may be continued if necessary as described below. It is also helpful if the robot knows what direction it is facing (north, south, etc. )
An algorithm for searching for the goal is as follows.
Empty the memory of the robot.
Push the current cell onto the current path.
Enter this cell into the "visited" set.
If more than one of the four directions is not obstructed, push the adjacent
cell in all but one of the free directions onto the trials path. (It now has
0-3) items. Push the current cell onto the trials path. Push the cell in the
remaining direction onto the trials path.
Otherwise, if only one direction was free then push the adjacent cell in that
direction onto the trials path.
While the trials path is not empty and we are not at the goal do
Pop a cell from the trials path.
Push it into the current path and move to that cell (moving in some direction,
of course).
Enter this cell into the visited set.
If this is the goal then quit. The goal has been found.
Otherwise, If more than one of the three directions to its left, front, and
right are not obstructed and have not been visited then push all but one of
them onto the trials stack and push the current cell on top of them.
Otherwise, if exactly one is free and not visited then simply push it onto
the trials path (i.e. push the cell in that direction).
Otherwise, if none of these directions are free and not visited, then back up
by popping the current path and moving to the corresponding cell until the
top of the current path matches the top of the trials path. Leave this cell
in the current path. Then pop the trials path.
A mapper is a specialized robot whose purpose is not to find the goal, but to traverse every reachable cell in the maze and to create a map of the maze as it does. A map is like a maze except that its cells are initially "unknown" and they are eventually marked as "reachable",
"goal", or "obstructed".
A seeker is a specialized robot that has a map of the maze in its memory and uses the map to find the goal as efficiently as it can.
Build a maze class and one or more of the robot classes. Try to improve the searching algorithm.
Many real world situations may be simulated using a set of queues that interact with each other. College registration is one system that is easily modeled by this technique. A collection of queues will be called a queuing system. Each of the queues are named or numbered and each represents a service that might be provided to one client at a time. If a client arrives for service and another client is being served then the new arrival waits by being inserted into the queue. The server then dequeues and item (client) when it is finished with the item currently being served which can take a variable amount of time. Each client arrives at the queuing system with a list of the queues that it must visit in the order that they must be visited. They leave the system when they have received service from each of the queues in their list. Each time they finish receiving service from one server they present themselves at the next one on their list.
The purpose of running the simulation is to determine certain statistics on the time behavior of the system. Total time to process a certain set of clients is one such statistic. Also total time for each client could be determined.
A clock is used to control the simulation. A clock is an object that responds to the following two messages.
Advance Time (advance the clock by some fixed amount) Get Time (return the current clock time)
The queuing system simulation proceeds by executing the following algorithm.
While there are still clients in the system do
Advance the time
For each queue do
ServeClient
If we are serving a client then
Check the clock against the termination time of this client
If time is up then release the client
If now free and queue is not empty then
Dequeue one client from the queue.
Compute the finish time for this client as a random number between limits
appropriate for this server.
When a client is released from a server it executes the following.
If the list of queues to be visited is not empty then remove the next one and enqueue on that queue.Otherwise mark the completion time by consulting the clock and wait on (insert self into) a list so that termination statistics may be computed when all clients finish.
Build such a system and test it.
5. Huffman Encoding and Decoding Problem
It is a common occurrence for us to have a text file of some kind that we want to compress, so it will take up as little space a possible. Perhaps this is because we want to save on storage space or charges or because we are about to send the file over an expensive phone link.
You probably know that computers use some sort of numeric encoding to represent characters - EBCDIC and ASCII are the two most popular ones. These encodings all have the property that any legal character is represented by the same number of bits (7 bits in ASCII, 8 in EBCDIC). This makes these encodings convenient to use, but also makes them somewhat redundant: if we could come up with an encoding that uses only a few bits for common characters like E or T, it would more than make up for a corresponding growth in the encodings for rare letters like X or Q.
One way to think about the notion of character encodings is to consider a tree structure where 0 means "go left" and 1 means "go right". If I am interested only in the letters ABCDEFGH, I could assign them three-bit codes as follows:
A 000 E 100 B 001 F 101 C 010 G 110 D 011 H 111This corresponds to the tree structure in Figure 5.5, where each code for a letter is represented by the path from the root to the corresponding letter.
If we know that E happens a lot more often than G, we might want to distort this tree, so that E is fewer steps from the top and G is correspondingly more. The tree in Figure 5.6 is the best tree possible given the actual English frequencies of these eight letters. This gives the encodings:
A 11 E 01 B 00000 F 0001 C 100 G 00001 D 001 H 101
One thing to notice is that the numerical order is no longer the same as the alphabetical order. However, since E is about eight times as common as G, we can see that we will use a lot less space. The word GEEEEEEEE required 27 bits before, but only 21 now. (In practice, compression of better than 50% is common.)
If we know the expected frequencies of characters in the file, we can use an encoding that gives us the smallest expected file length. Such an encoding is called a "Huffman encoding" and the tree that summarizes such an encoding is called a "Huffman tree".
We can use a table or dictionary of Huffman codes to compress a file. For instance, if the file consisted only of the word CHAFED, we could look up C and output 100, look up H and output 101, and so on, producing the output file 10010111000101001. This is slightly compressed, requiring only 17 bits in contrast to 18 needed if we use fixed-length codes, or 42 if we use ASCII.)
To decompress the compressed file, it is convenient to use the tree. We start at the root and look at the first bit of the compressed file. Since it is a 1, we move down to the right and read the second bit. Since it is a 0, we move left. The third bit is 0, so we move left again, which brings us to the C. Thus the first letter is C; we output it and start over at the root again.
Huffman's Tree Building Algorithm
1. Collect all the characters you want to encode and assign a weight to each, based upon the expected frequency of each character in a typical input file. Frequencies are given below.
2. Create a list of one node binary trees with these weights and characters.
3. Repeat until there is only one node left in the list (n-1 times):
a. Remove the two nodes with the smallest weights and connect them to a common parent.
b. Assign the weight of the parent to be the sum of the weights of the two children.
c. Insert this new tree into the list of trees.
4. The remaining tree is the Huffman tree.
Relative frequencies of allowed character set:
73 9 30 44 130 28 16 35 74 2 A B C D E F G H I J 3 35 25 78 74 27 3 77 63 93 K L M N O P Q R S T 27 13 16 5 19 1 U V W X Y Z 2 2 9 15 258 20 ( ) , . space eolnNOTE: End-of-line is not treated as a character in many systems. It is present here because we want our compressed files to record the locations where line boundaries appeared so that we can restore those line boundaries when we decompress the files. The easiest way to do this is to choose some character not shown above (for ex, '$') to stand in for eoln in the Huffman tree. When an end-of-line condition (eoln) is detected on input, it should be encoded with the compressed code. When the compressed code for eoln is detected during the decode operation, start a new line of decoded output.
Here is the beginning of an example of this. After performing step three for the first time we have
After performing it the second time we have2 2 3 3 3 5 9 9 and so on until 130 258 ( ) * K Q X B , E space / \ Z J
And after performing it the third time we have3 3 3 4 5 9 9 and so on until 130 258 * K Q * X B , E space / \ / \ Z J ( )
3 4 5 6 9 9 and so on until 130 258 Q * X * B , E space / \ / \ ( ) * K / \ Z JAfter you have built the tree, you must traverse it recursively to extract the encodings. An abstract version of this part might look like this:
ExtractCodes (node p, path fromroot ) IS -- fromroot contains the path from the root to node p if (p is a leaf node) then announce that the code for character in p is fromroot else ExtractCodes(LeftChild(p), fromroot extended with 0); ExtractCodes(RightChild(p), fromroot extended with1); end ENDEven though this doesn't discuss how to implement a "node" or a "path", this is the correct algorithm for extracting the codes. The action "announce" might mean simply printing the code found, or might mean adding it to a table or dictionary.
Encoding and decoding
Once the encoding table is built, encoding simply involves a table look-up for each character.
To decode an encoded file, one must examine the bits of the file and use the Huffman tree to decode. An algorithm follows:
Huffman Decode:
1. Initialize p to the root of the Huffman tree. 2. While the end of the message has not been reached Let x be the next bit in the string. If x = 0 then set p to LeftChild(p) else set p to RightChild(p) If p is a leaf then Display the character associated with that leaf Reset p to the root of the Huffman tree
Build and test a program or set of programs to:
a) Using the frequencies given above, construct a Huffman tree using the algorithm described above.
b) Traverse the Huffman tree to make a table of the Huffman codes.
c) Use the table of Huffman codes to translate an input file into compressed form. Use any input text you like, but make sure it contains only those characters you have codes for. This input file should be at least ten lines long.
d) Use the Huffman tree to translate the compressed file back into normal text.
Your program should print the codes assigned to the alphabet above, and should display the original file in character form, the Huffman encoded file in binary form (that is, as zeroes and ones), and the decompressed file in character form. The decompressed file should, of course, be identical to the original.
Your program should also print the length of the original message (in characters) and the length of the compressed file (in bits). Since the alphabet we are using has 32 characters, we would ordinarily need five bits per character. How does this compare with the translation done according to your Huffman codes?
Notes:
1. Since you need to do insertions and deletions from the list of partial trees, it may be helpful if you organize the partial trees into a list, sorted by weight; i.e. when you initially build it, use an InsertInOrder procedure. If you then keep it in order, all deletions are from the front of the list, and insertions are done using InsertInOrder.
2. Since you will really be writing out ASCII or EBCDIC zeroes and ones to create the compressed file, the output file will actually be considerably larger that the original file. To create a truly compressed file requires knowledge of how the system stores values in memory and how they are written to a file, and the use of low level bit manipulations.
3. As you build the tree, the important data for the interior nodes is the weight, while in the leaves, the only important data is the character. It's easiest to make all values inserted into the tree to be objects with fields `weight' and `character' and use whichever is appropriate. Even better is to use two different object types. In the initial list of trees, each tree would consist of a single node with both a weight and a character.
4. You should implement writeIt for the new object types so that it will be easy to write out the Huffman trees.
5. A more sophisticated version of this, which is appropriate for long, unusual files, is to first scan the file to be compressed, determining the actual frequency of the characters. Then determine a corresponding Huffman code tailored to that file. Then, before sending the file using this encoding, send the code itself (or equivalently the frequency distribution used to build it) in the clear (unencoded). For a file that is long and contains character distributions significantly different from English prose, this can represent a large savings.
(Thanks to David Wall of Digital Equipment Corporation for this assignment.)
6. Simulation of a simple computer system.
A simple computer system consists of a processor, with its associated peripherals, that is capable of processing one job at a time. However, It is desirable for the processor to share, or multiplex, its time among the various jobs, so that when a process requests input or output (I/O) the processor may execute another process while waiting for the I/O request to complete. The reason for this is that I/O is so much slower than the processor that if the processor simply waited, too much time would be wasted and system throughput would be reduced to the speed of the slowest device. A processor contains a job queue that holds jobs that are ready to be executed but not currently being executed. We would like to have a simulator of such a system so as to get statistics on the time required to complete a job or a certain mix of jobs. For this purpose, the processor will provide two services to the jobs: execute and processIO. While a job executes the system advances a clock. Each time a job executes the system gives it a certain amount of time, and when the job currently executing exceeds that time it is temporarily halted and placed on the job queue. It will be resumed when it reaches the head of the queue. Whenever a job requests I/O by executing processIO it is also halted and placed on the queue. The processor always knows the current job, and when it puts a job on the queue it extracts a new current job from the queue. The processor is also responsible for placing new jobs on the queue when the time comes for them to be executed.
Each job has a job number, a start time and an expected time requirement. This is the average value of the time the job would take to execute if it were not interrupted for I/O and had exclusive use of the processor. In reality the actual amount of time needed by a job when it runs will always exceed this time requirement because the delays are inevitable if the job does any I/O and very likely even if it does not. The job also has a parameter that measures the probability that it will do I/O in a fixed time interval, or "clock tick." The job must provide services to the processor so that the latter may discover the job number of a job and its parameters. It should also permit a processor to reduce its time requirement toward zero so that as the clock runs the processor will know when the job has completed.
When a job gets access to the processor it can be thought of as executing the following "program"
WHILE timeRequrement > 0 DO processor . execute (); IF randomNumber () < I_OProbability THEN processor . processIO (); END; END;The function randomNumber is assumed to return a random real number in the range of zero to one. Random integers may be obtained from the system function rand in <stdlib.h>. Suitable processing will transform them into the required float values.
The processor may be assumed to execute the following pseudocode program.
REPEAT advanceClock; IF new_job_waiting THEN enter_it_into_queue; END; IF no_current_job THEN dequeue_a_current_job; END; IF current_job_finished THEN terminate_it; ELSIF current_job_requesting_IO THEN queue_it; ELSE advance_time_of_current_job; END; UNTIL no_jobs_in_queue;When a job terminates its statistics can be printed.
A refinement of the above is to make the I/O processing more realistic by requiring a time requirement for completion of the request to be submitted when the I/O request is submitted. Then when the processor removes a job from the queue it can check to see if the previous I/O request has completed, and if not will reinsert the job on the queue and process another. Note that you must be a bit careful here that you don't create an infinite loop of checking without advancing the clock.
Some Sample Test data: Job Execution I/O Entry Number Time Prob. Time 1 5 .6 1 2 1 .2 2 3 10 .1 4 4 4 .4 5 5 3 .2 7 6 8 .3 9 7 2 .5 10 8 9 .9 12 9 6 .2 13 10 5 .4 15