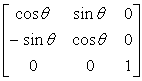|
Part I - 2D
Geometric Transformations |
Hearn and Baker – Chapter 5
· Geometric
Transformations – alter coordinate description of objects
· Basic
Transformations => Translation, Rotation, Scaling
Translation
·
Translation of a data point is accomplished through the
addition of factors to the x and y coordinates.
·
P(x,y) becomes P ' (x',y' )
x' = x + Tx
y' = y + Ty
·
Tx and Ty are the
shift in x and y coordinates.
·
Example: translating a square (Blue) by adding Tx = 3 to
each x coordinate, and Tx = -3 to
each y coordinate (Red).
Scaling
·
Scaling proceeds by multiplying the coordinate values by Sx and Sy , scaling
factors in the x and y axis directions
x' = x
Sx
y' = y
Sy
·
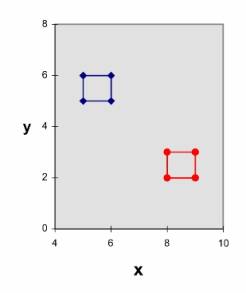
Example: scaling a square by Sx = 2 and Sy = 3.
|
Sx |
Sy |
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
Original Points |
|
Absolute Scaling |
||
|
x |
y |
|
x' |
y' |
|
1 |
1 |
|
2 |
3 |
|
2 |
1 |
|
4 |
3 |
|
2 |
2 |
|
4 |
6 |
|
1 |
2 |
|
2 |
6 |
|
1 |
1 |
|
2 |
3 |
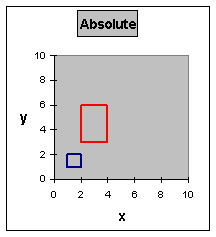
Note: square is not larger but also shifted twice
the distance from the origin in x,
and thrice the distance in y.
Rotation
·
Rotation of a data point P(x,y) about the origin in the
counterclockwise direction to a new position P' (x',y') :
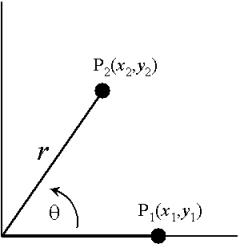
x' = r cos q
y' = r sin q
o Note: This is the transformation from polar coordinates to Cartesian
Coordinates where x=r
·
What if point is in xy plane?
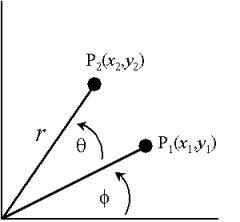
Begin with…
x' = r cos (q + f)
y' = r sin (q + f)
Use trigonometric identities
cos (q + f) = cos f cos q - sin f sin q
sin (q + f) = cos f sin q + sin f cos q
Substitute
above into equations for x' and y' gives …
x' = r cos f cos q - r
sin f sin q
y' = r cos f sin q + r
sin f cos q
And …
cos f = x / r
sin f = y / r
Subsitute
into above…
x' = r (x
/ r )cos q - r (y / r) sin q = x cos q - y sin q
y' = r (x /
r )sin q + r
(y / r) cos q = x sin q + y cos q
o
where x,y are the starting coordinates
o
q is the angle
through which the point is rotated to give x
',y '.
·
Example:
General 2D Transformations
o
Simple primitive geometric transformations may be combined
to create more complex and useful operations
o
e.g. an unwanted translation is a byproduct of scaling.
o
Solution
o
Translate object to the origin of the coordinate system
o
Scaling object
o
Translating object back to its original position
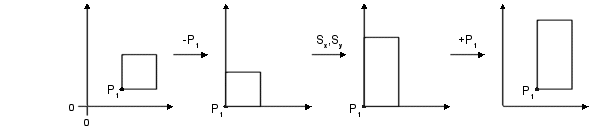
o
Step 1: Tx and Ty
are set to the x,y coordinates of P1
and subtracted from all points.
Places P1
at position (0,0) with all other points relative to it.
o
Step 2: Scaling is performed in, with Sx
= 2 and Sy = 3.
Object has
now been expanded relative to point P'1 that remains at the origin.
o
Step 3: object returned to the starting
point P1 by adding in the original x,y coordinates of P1 .
o Although scaling is executable as a three-step process, it is more efficient to combine them into a single transformation.
o Must recast the transformation into matrix notation.
o Look back at the two formulas for the rotation transformation
o New data point P ' consists of an ordered pair of numbers x',y' that may be written in matrix form as
![]()
o
Both matrices are one row by two columns => Row
Vectors
o
Matrix on RHS equal sign is an expansion of the left.
o
Element (1,1) of the first matrix equals element (1,1) of
the second.
o
Element (1,2) of the first matrix equals element (1,2) of
the second.
o
It is possible to decompose the RHS into two matrices
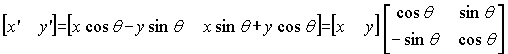
o x' results from multiplying each element in the coordinate
data row matrix with its respective element in the first column of the rotation
matrix and summing them;
o y' results from multiplying by the respective elements
in the second column and summation.
o A more
succinct vector notation is
![]()
where
R is the rotation matrix
X and X' contain the original and transformed data
o Matrix
multiplication:
o
proceeds from left to right
o
adheres to the associative law of multiplication,
o
does not obey the commutative law
o In general, C = AB is given
by
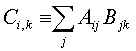
Example,
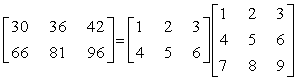
·
Can represent data as Column Vectors
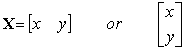
Row Vector Column Vector
·
And
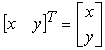 The column
vector is the transpose of the row vector
The column
vector is the transpose of the row vector
·
Transpose operation interchanges rows and
columns of matrix such that
xij = xji
· Transpose operation
interchanges multiplation of matrices
(RP)T = PTRT
·
Can rewrite matrix representation of rotation:
So…
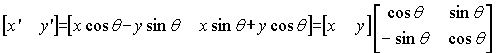
becomes
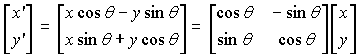
Scaling is decomposed in the same fashion, giving
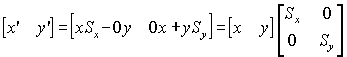
with
![]()
or in
transposed form
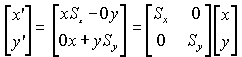
with
![]()
Homogeneous Coordinates and Transformations
· Problem:
Translation does not decompose into a 2 x 2 matrix
·
Solution: Represent Cartesian Coordinates (x,y) as
Homogeneous Coordinates (xh, yh, h)
Where
x = xh / h , y =
yh / h
typically h = 1
and … each data point is (x,
y, 1 )
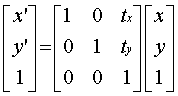
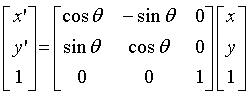
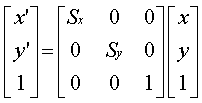
Composite Transformations
1. Example:
General Fixed-point Scaling.

·
Three operations
![]()
These
correspond to the three steps of translation to the origin, scaling, and
translation back, with matrices
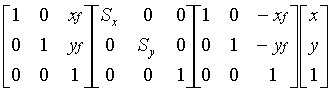
3rd 2nd 1st
Multiplying
through from left to right gives the final matrix
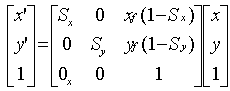
with final
equations
x' = xSx - xf Sx +
xf
y' = ySy - yf Sy +
yf
· If the object is already at the origin, xf = yf = 0, the formula reduces to the original scaling formula.
· Example:
|
Sx |
Sy |
|
|
|
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
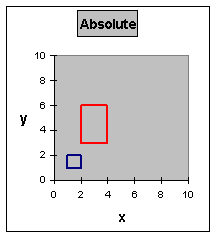
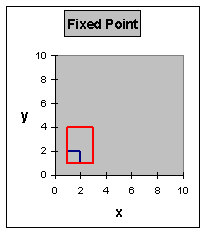
Original Points |
|
Absolute Scaling |
|
Fixed Point |
|||
|
x |
y |
|
x' |
y' |
|
x' |
y' |
|
1 |
1 |
|
2 |
3 |
|
1 |
1 |
|
2 |
1 |
|
4 |
3 |
|
3 |
1 |
|
2 |
2 |
|
4 |
6 |
|
3 |
4 |
|
1 |
2 |
|
2 |
6 |
|
1 |
4 |
|
1 |
1 |
|
2 |
3 |
|
1 |
1 |
2. General Pivot Rotation (Rigid-Body Transformation)
·
Rotate object about a
point (xr, yr)
Steps:
1. Translate to Origin
2. Rotate about Origin
3. Translate back
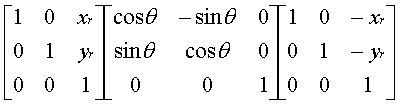
·
Final matrix:
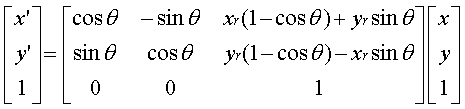
·
Final Formulas
x' = x cos q - y sin q + xr(1- cos q) + yr
sin q
y' = x sin q + y cos q + yr (1 - cos q) – xr
sin q
·
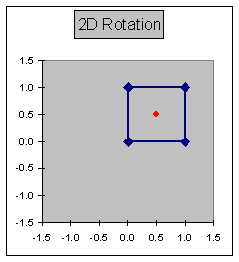
Example
Starting Point:
|
|
Angle |
|
xc |
yc |
|
|
0 |
|
0.5 |
0.5 |
|
|
|
|
|
|
|
Original |
|
|
Transformed |
|
|
x |
y |
|
x' |
y' |
|
0.0 |
0.0 |
|
0.00 |
0.00 |
|
1.0 |
0.0 |
|
1.00 |
0.00 |
|
1.0 |
1.0 |
|
1.00 |
1.00 |
|
0.0 |
1.0 |
|
0.00 |
1.00 |
|
0.0 |
0.0 |
|
0.00 |
0.00 |
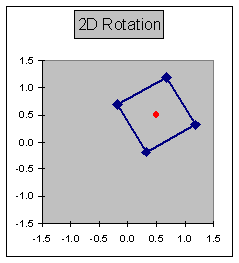
Rotation
Angle: 30 Degrees
|
|
Angle |
|
xc |
yc |
|
|
30 |
|
0.5 |
0.5 |
|
|
|
|
|
|
|
Original |
|
|
Transformed |
|
|
x |
y |
|
x' |
y' |
|
0.0 |
0.0 |
|
0.32 |
-0.18 |
|
1.0 |
0.0 |
|
1.18 |
0.32 |
|
1.0 |
1.0 |
|
0.68 |
1.18 |
|
0.0 |
1.0 |
|
-0.18 |
0.68 |
|
0.0 |
0.0 |
|
0.32 |
-0.18 |
Other Transformations
·
Reflection
e.g. reflection about y = 0
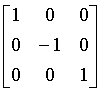
e.g. reflection about y = x
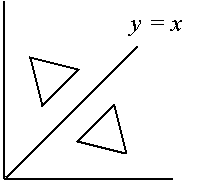

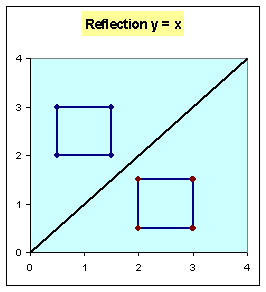
· Example:
|
Original |
Data |
|
Reflection
|
y = x |
|
x |
y |
|
x' |
y' |
|
2.0 |
0.5 |
|
0.5 |
2.0 |
|
3.0 |
0.5 |
|
0.5 |
3.0 |
|
3.0 |
1.5 |
|
1.5 |
3.0 |
|
2.0 |
1.5 |
|
1.5 |
2.0 |
|
2.0 |
0.5 |
|
0.5 |
2.0 |
·
Shear
Shape Distortion
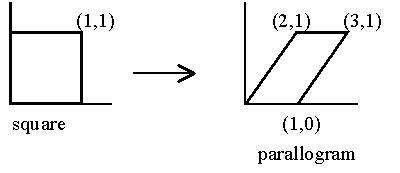
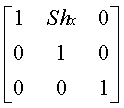 x shear
x shear
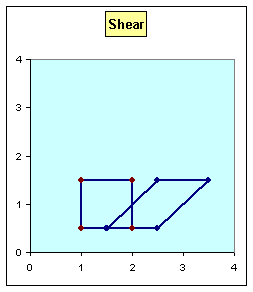
Example:
|
Shear |
|
|
|
|
|
Shx |
Shy |
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
Original |
Data |
|
Final |
Data |
|
x |
y |
|
x' |
y' |
|
1.0 |
0.5 |
|
1.5 |
0.5 |
|
2.0 |
0.5 |
|
2.5 |
0.5 |
|
2.0 |
1.5 |
|
3.5 |
1.5 |
|
1.0 |
1.5 |
|
2.5 |
1.5 |
|
1.0 |
0.5 |
|
1.5 |
0.5 |
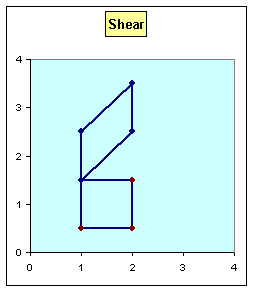
· What would
y shear matrix look like?
|
Shear |
|
|
|
|
|
Shx |
Shy |
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
Original |
Data |
|
Final |
Data |
|
x |
y |
|
x' |
y' |
|
1.0 |
0.5 |
|
1.0 |
1.5 |
|
2.0 |
0.5 |
|
2.0 |
2.5 |
|
2.0 |
1.5 |
|
2.0 |
3.5 |
|
1.0 |
1.5 |
|
1.0 |
2.5 |
|
1.0 |
0.5 |
|
1.0 |
1.5 |
Transformations between coordinate systems
· Graphic
applications need transformation:
· from one
coordinate system to another
· from one
reference frame to another
· e.g. Two
Cartesian Systems:
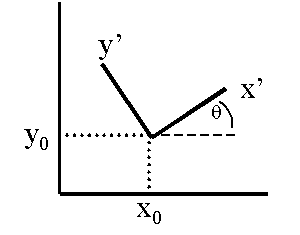
1.
Translate to origin
2.
Rotate clockwise x’ into x
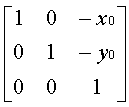
R(-q) =