|
Two Dimensional Viewing |
H&B Chapter 6
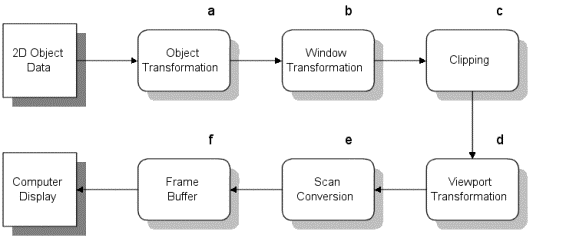
Viewing Pipeline
Window world coordinate area for display
Viewport area on display device to which window is mapped
Window
what is viewed
Viewport
where it is displayed
Viewing Transformations mapping part of a world coordinate scene to device
coordinates
aka Window-Viewport
Mapping

2D Viewing-Transformation Pipeline

Viewing Coordinate Reference Frame
Procedure:
- Set up viewing-coordinate origin at some world
position Po(xo,yo)
- Set up orientation of reference frame
e.g.
could set up view-up vector
can
compute component of u = (ux, uy) & v = (vx,vy)
- obtain matrix for converting world coordinates
to viewing coordinates
i. translate viewing origin to world origin
ii. rotate to align two coordiate reference frame
![]()
Window-to-Viewport Coordinate Transformation
- Device transformations using:
- Xwl, Xwh, Ywl, Ywh
- Xvl, Xvh, Yvl, Yvh
- Use Transformation:
1. Set up windowvl
2. Translate window
3. Scale to normalize
4. Scale to viewport
5. Translate to Viewport

![]()
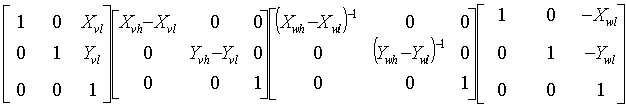
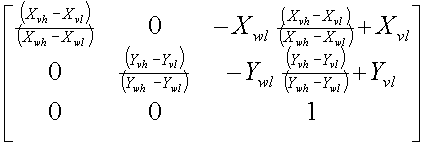
What are the final
formulas?
Xv = [(Xvh - Xvl)/(Xwh - Xwl)]
(X - Xwl) + Xvl
Yv = [(Yvh - Yvl) / (Ywh - Ywl)]
(Yw - Ywl) + Yvl
|
Window-Viewport Mapping |
|
|
|
|||
|
|
|
|
|
|
|
|
|
Xwh |
Xwl |
Ywh |
Ywl |
Xwh-Xwl |
Ywh-Ywl |
|
|
7.5 |
2.5 |
9 |
2.5 |
5 |
6.5 |
|
|
|
|
|
|
|
|
|
|
Xvh |
Xvl |
Yvh |
Yvl |
Xvh-Xvl |
Yvh-Yvl |
|
|
900 |
400 |
700 |
400 |
500 |
300 |
|
|
|
|
|
|
|
|
|
|
No. |
x |
y |
X-Viewport |
Y-Viewport |
|
|
|
1 |
1.0 |
4.0 |
250.000 |
469.231 |
|
|
|
2 |
4.0 |
10.0 |
550.000 |
746.154 |
|
|
|
3 |
8.0 |
8.0 |
950.000 |
653.846 |
|
|
|
4 |
8.0 |
4.0 |
950.000 |
469.231 |
|
|
|
1 |
1.0 |
4.0 |
250.000 |
469.231 |
|
|
|
|
|
|
|
|
|
|
|
Window Coordinates |
Viewport Coordinates |
|
|
|||
|
x |
y |
|
x |
y |
|
|
|
2.5 |
2.5 |
|
400 |
400 |
Window/Viewport |
|
|
2.5 |
9 |
|
400 |
700 |
Outline |
|
|
7.5 |
9 |
|
900 |
700 |
|
|
|
7.5 |
2.5 |
|
900 |
400 |
|
|
|
2.5 |
2.5 |
|
400 |
400 |
|
|
|
|
|
|
|
|
|
|
|
1.0 |
4.0 |
|
250 |
469 |
Data Points |
|
|
4.0 |
10.0 |
|
550 |
746 |
|
|
|
8.0 |
8.0 |
|
950 |
654 |
|
|
|
8.0 |
4.0 |
|
950 |
469 |
|
|
|
1.0 |
4.0 |
|
250 |
469 |
|
|


Clipping Operations
Clipping Algorithms -> procedure that identifies portions of picture either
inside or outside specified regions
Clip Window -> region against which an object is clipped
Applications of Clipping:
- Extracting part of defined scene for viewing
- Identifying visible surfaces in 3D Views
- Anti-aliasing line segments or object boundaries
- Creating objects using solid modelling
procedures
- Drawing and painting operations
·
Clipping operations
eliminate everything outside window
·
Two Approaches:
- Clip word coordinates -> only contents of
window interior mapped to device coordinates
- Map all world coordinates to device coordinates
-> then clip against viewport boundaries
·
Raster systems ->
clipping part of scan conversion
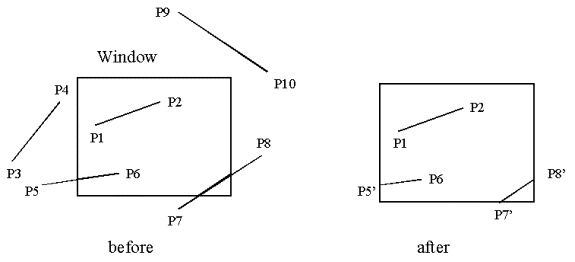
Point Clipping
Rectangular clipping window
Point P(x,y) saved for
display IF
Ywl
<= y <= Ywh
Line Clipping
Line Clipping Procedure:
1. Test line segment to determine if it resides
completely inside clipping window
2. Test to see if it is completely outside
3. It we are unable to tell, perform intersection tests
Inside-Outside Test
·
Check both endpoints
-> if both P1 and P2 are within boundaries line is saved
·
If both endpoints
outside drop line segment
·
Remaining may require
calculation of multiple intersections
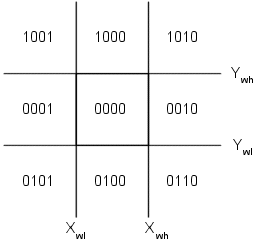
Sutherland-Cohen Line Clipping
·
Every line endpoint is
assigned a 4 bit Region code.
·
The bit is set
depending on the location of the endpoint with respect to that window component
as shown below:
|
Bit 1: Left of window Bit 2: Right of window Bit 3: Below window Bit 4: Above window
|
|
|
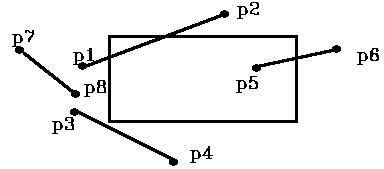
Example: P1 -> 0001, P 2 -> 1000 P3 -> 0001, P4 -> 0100 P5 -> 0000, P6 -> 0010 P7 -> 0001, P8 -> 0001 |
|
Determine
the bit code by testing the endpoints with window as follows:
o
If x is less than Xwl
then set bit 1
o
If x is greater than
Xwh then set bit 2
o
If y is less than Ywl
then set bit 3
o
If y is greater than
Ywh then set bit 4
§
Possible Algorithm
o
Calculate difference
between endpoint coordinates and clipping boundary
o
Use sign bit of
difference to set region code
x Xwl bit 1
Xwh x bit 2
y Ywl bit 3
Ywh y bit 4
o
Determine Visibility
·
Any line whose
endpoints have region codes of 0000 is visible
o
Any lines that have 1
at same bit position for each endpoint are outside
·
Use AND operation as
test
1001
0101
0001
·
If result is not zero
line is completely outside
o
All other lines must be
tested against boundaries -> one at a time
§
Procedure:
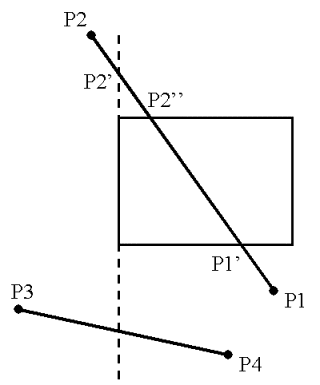
o Begin with
P1 and lower boundary and check against left, right, and bottom boundaries
o Find
intersection point P1 with bottom boundary and replace P1 with P1
o Do same
with P2 but we find two intersections p2 and p2
o P2 is
above window but P2 is on window boundary
Computing line intersections
§
Need to fined (x,y)
position alone a line segment
§
We know
y =
mx + b
m =
( y2 y1) / ( x2 x1 )
b =
y1 m x1
so
y =
m x + y1 m x1
y = y1 + m ( x x1)
§
substitute for x
=> Xwh or Xwl to calculate y coordinate of intersection
also
x =
x1 + ( y y1) / m
§
substitute for y
=> Ywh or Ywl to calculate x coordinate of intersection
§
Example:
P1 : (1, 4 ) and P2 : ( 4, 10 )
|
Xwh |
Xwl |
Ywh |
Ywl |
|
7.5 |
2.5 |
9 |
2.5 |
Answer:
Intersection with Ywh == x = 3.5
Intersection with Xwl == y = 7
So
P1 = ( Xwl, 7) = ( 2.5, 7 )
P2 = ( 3.5, Ywh ) = ( 3.5, 9 )
§
Splitting Concave Polygons
§
Identify concave polygons by calculating cross products of
successive edge vectors
§
If z value of some cross products is positive while others
are negative, concave polygon exits.
(assume no three successive vertices are collinear =>
gives 0 crossproduct)
Example:
z-component processing

(E1 X E2) > 0
(E2 X E3) > 0
(E3 X E4) < 0
(E4 X E5) > 0
(E5 X E6) > 0
(E6 X E7) > 0
§
Cross product:
V1 X V2 = u |V1||V2| sinq
where u is unit vector perpendicular to V1 and V2
V1 X V2 = ( V1y V2z V1z V2y, V1z
V2x V1x V2z, V1x V2y V1y V2z )
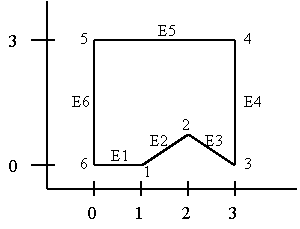
E1 = (1, 0, 0)
E2 = (1, 1, 0)
E3 = (1, -1, 0)
E4 = (0, 2, 0)
E5 = (-3, 0, 0)
E6 = (1, -2, 0)
(E1 X E2) = (0, 0, 1)
(E2 X E3) = (0, 0, -2)
(E3 X E4) = (0, 0, 2)
(E4 X E5) = (0, 0, 6)
(E5 X E6) = (0, 0, 6)
(E6 X E7) = (0, 0, 2)
Since E2 X E3 z-value < 0 must
split polygon along line E2
Must determine intersection of line
with edge E4
Use slope-intercept form of line:
y = max + ba y = mbx + bb
max + ba = mbx + bb
x = ( bb - ba ) / (ma - mb )
and
x = ( y - ba
)
/ ma x = ( y bb ) / mb
( y - ba ) / ma = ( y bb
)
/ mb
y = (ma bb mb ba ) / (ma - mb )
§
Alternative method for splitting concave polygons
1.
Rotational Method:
2.
Proceed counterclockwise
3.
Translate each polygon vertex Vk in sequence to origin
4.
Rotate cloackwise so next vertex is on x axis
5.
If next vector Vk+2 is below axis, polygon is concave
e.g.

§
can fined, since (x, y=0), substitute into
x = x1 + ( y y1
)
/ m
so
x = x1 - y1
/ m
Polygon Clipping
§
Polygon boundary
processed with a line clipper appears as series of unconnected line segments
e.g.
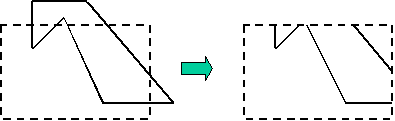
Need to display a bounded area after
clipping
Need algorithm that will
generate one or more closed areas that can be scan converted
Sutherland Hodgeman Polygon Clipping
§
Clip polygon against
all four edges
§
Each successive clipped
polygon sent to next edge

4 Vertex Processing Cases
- 1st outside, 2nd inside
intersection
points and inside points added to output vertex list
- 1st inside, 2nd inside
2nd
vertex added to output vertex list
- 1st inside, 2nd outside
intersection
added to output vertex list
- 1st outside, 2nd outside
nothing
added to output vertex list
e.g.