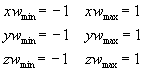Computer Graphics
|
3D Viewing
|
H&B Chapter 7
Projections
Coordinate
positions transformed to viewplane with parallel lines
- Perspective Projection
Coordinate
positions transformed to viewplane with converging lines
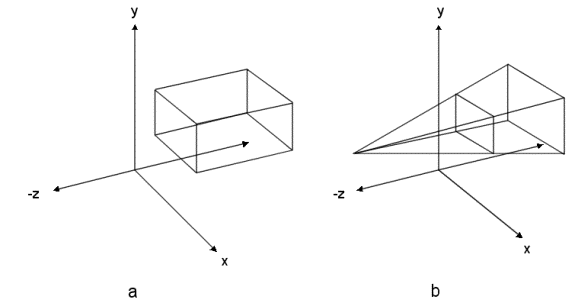
Parallel Projections
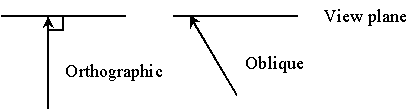
- Orthographic Projection => used for front,
side, back, top, bottom views
Transformation equations for parallel projection
Orthographic
Projection:
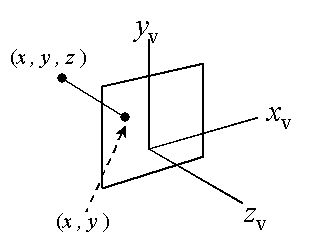
xp = x
yp = y
Oblique Projection
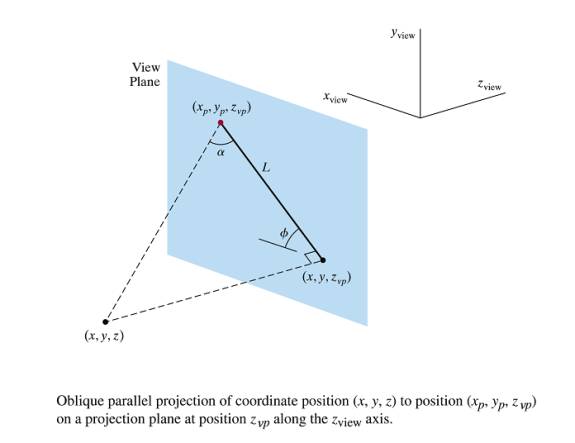
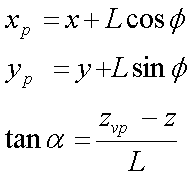
Perspective Projections – general case
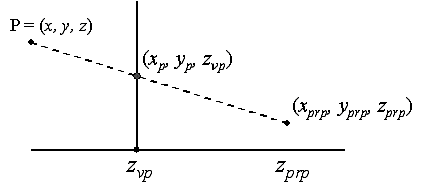
…where ( xprp, yprp, zprp
) is the perspective reference
point
Begin with parametric equation for line…
xp = x - (x – xprp)u
yp = y - (y – yprp)u
zp = z - (z – zprp)u
u = 0 -> 1
solve for u where zvp = zp (viewplane)
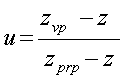
substitute in xp, yp equations
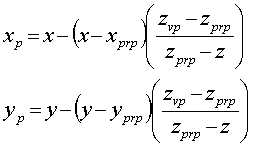
multiplying through and rearranging…
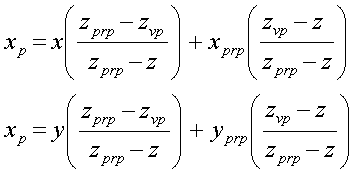
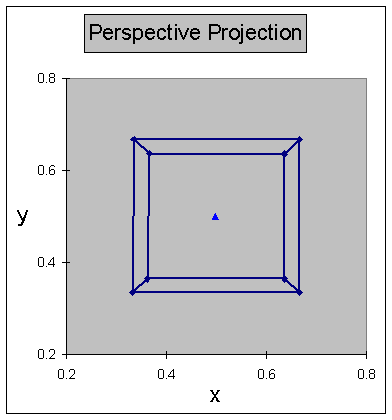
Special Case -- zvp = zp = 0
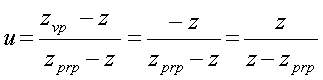
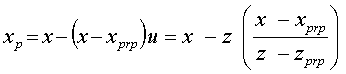
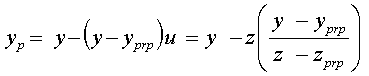
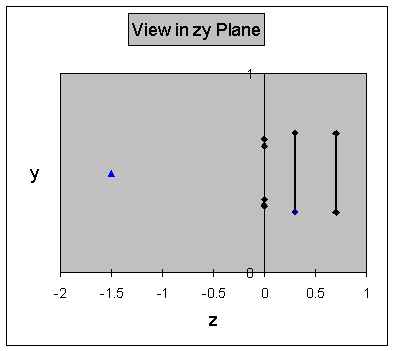
Example: Special Case where zvp = zp =
0
|
Perspective
Projection |
|
Xprp |
Yprp |
Zprp |
|||
|
|
|
|
|
|
0.5 |
0.5 |
-1.5 |
|
|
|
|
|
|
|
|
|
|
Point |
x |
y |
z |
|
x' |
y' |
z' |
|
1 |
0.30 |
0.30 |
0.30 |
|
0.33 |
0.33 |
0 |
|
2 |
0.30 |
0.70 |
0.30 |
|
0.34 |
0.67 |
0 |
|
3 |
0.30 |
0.30 |
0.70 |
|
0.36 |
0.36 |
0 |
|
4 |
0.30 |
0.70 |
0.70 |
|
0.37 |
0.64 |
0 |
|
5 |
0.70 |
0.70 |
0.70 |
|
0.64 |
0.64 |
0 |
|
6 |
0.70 |
0.30 |
0.70 |
|
0.64 |
0.36 |
0 |
|
7 |
0.70 |
0.70 |
0.30 |
|
0.67 |
0.67 |
0 |
|
8 |
0.70 |
0.30 |
0.30 |
|
0.67 |
0.33 |
0 |
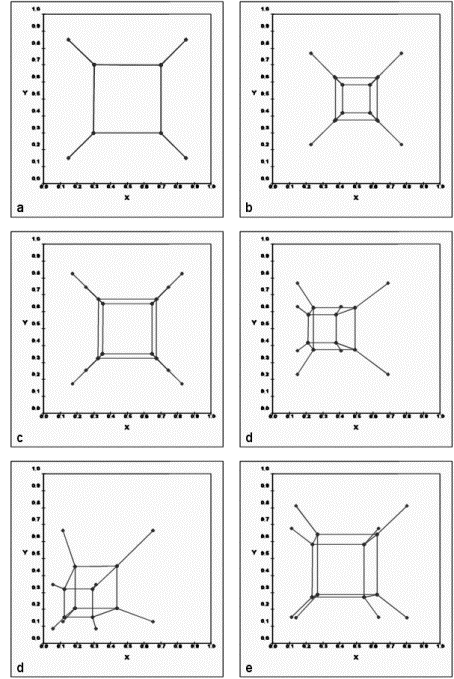
Example Too:
|
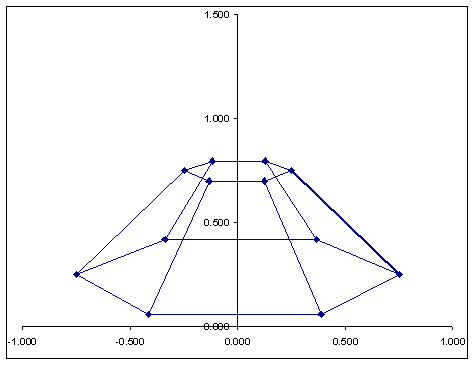
Surface of Revolution |
|
|
|
|
|
||
|
|
x1 |
y1 |
z1 |
|
x2 |
y2 |
z2 |
|
0 |
0.750 |
0.250 |
0.000 |
|
0.25 |
0.750 |
0.000 |
|
60 |
0.375 |
0.250 |
-0.650 |
|
0.125 |
0.750 |
-0.217 |
|
120 |
-0.375 |
0.250 |
-0.650 |
|
-0.125 |
0.750 |
-0.217 |
|
180 |
-0.750 |
0.250 |
0.000 |
|
-0.25 |
0.750 |
0.000 |
|
240 |
-0.375 |
0.250 |
0.650 |
|
-0.125 |
0.750 |
0.217 |
|
300 |
0.375 |
0.250 |
0.650 |
|
0.125 |
0.750 |
0.217 |
|
360 |
0.750 |
0.250 |
0.000 |
|
0.25 |
0.750 |
0.000 |
|
|
|
|
xc |
yc |
zc |
||||||
Perspective Projection
|
0.1 |
3 |
-10 |
||||||||
|
X1p |
Y1p |
|
|
X2p |
Y2p |
|
|||||
|
0.750 |
0.250 |
|
|
0.250 |
0.750 |
|
|||||
|
0.387 |
0.059 |
|
|
0.123 |
0.700 |
|
|||||
|
-0.415 |
0.059 |
|
|
-0.132 |
0.700 |
|
|||||
|
-0.750 |
0.250 |
|
|
-0.250 |
0.750 |
|
|||||
|
-0.340 |
0.418 |
|
|
-0.118 |
0.798 |
|
|||||
|
0.364 |
0.418 |
|
|
0.127 |
0.798 |
|
|||||
|
0.750 |
0.250 |
|
|
0.250 |
0.750 |
|
|||||
12.4 View Volumes and General Projections
- View window or projection window used to set up
telephoto or wide angle scene
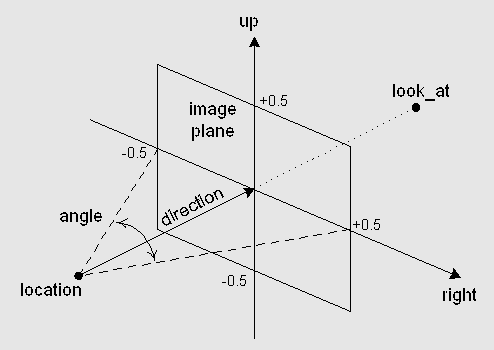
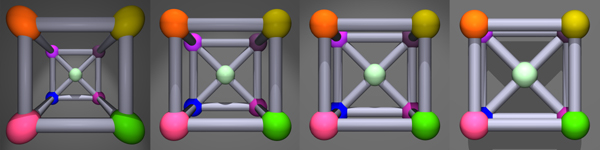
Focal Lengths and Angles of View
|
35mm Camera |
Focal Length(mm) |
Angle of View (Degrees) |
|
Extreme Telephoto |
800 |
3.5 |
|
|
400 |
6.0 |
|
|
200 |
12.5 |
|
Moderate Telephoto |
135 |
18.0 |
|
|
85 |
29.0 |
|
|
50 |
46.0 |
|
Normal |
43 |
53.0 |
|
Moderate Wide Angle |
24 |
84.0 |
|
Wide Angle |
18 |
94.0 |
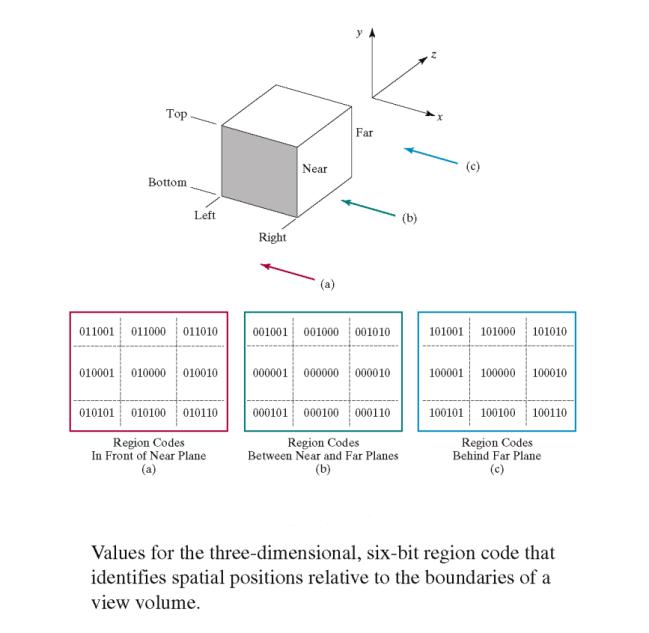
Viewing
- Edges of window parallel to x.y axes
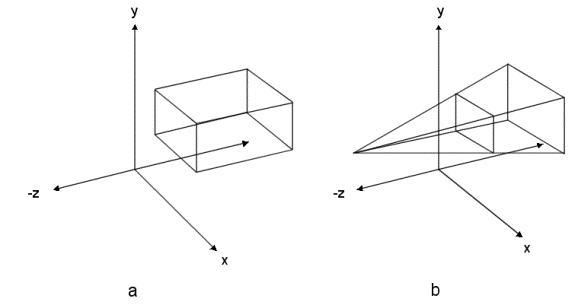
a –
parallelepiped b
– frustum
Symmetric Perspective-Projection Frustum
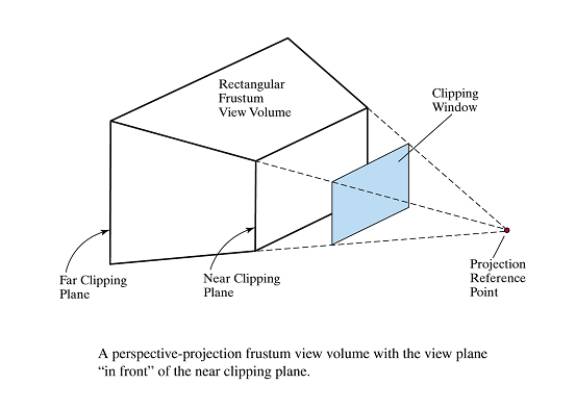
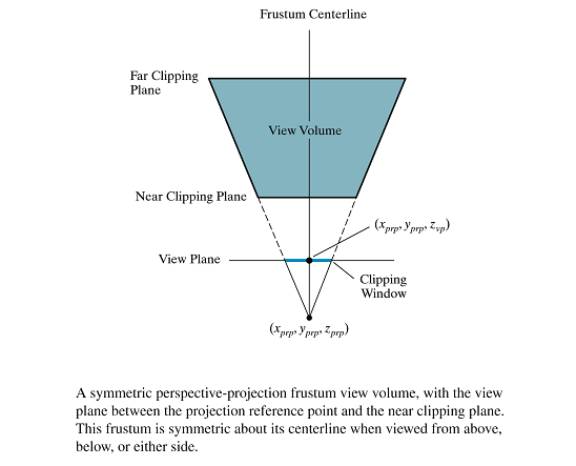
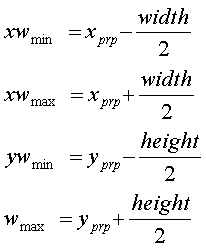
Window dimensions specify
field of view
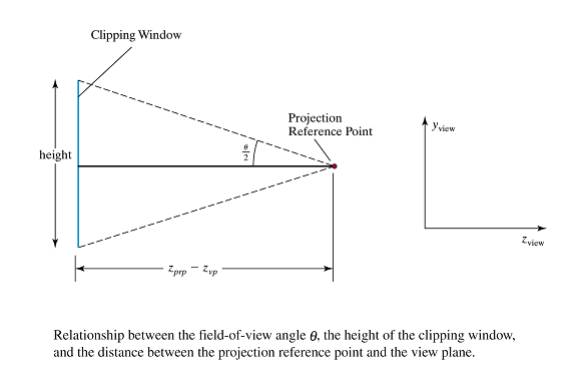
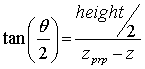
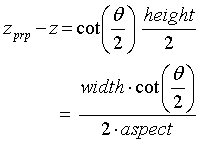
- Second equation used by graphics libraries (eg
OpenGL)
- These formulas are substituted into the
perspective projection formulas above.
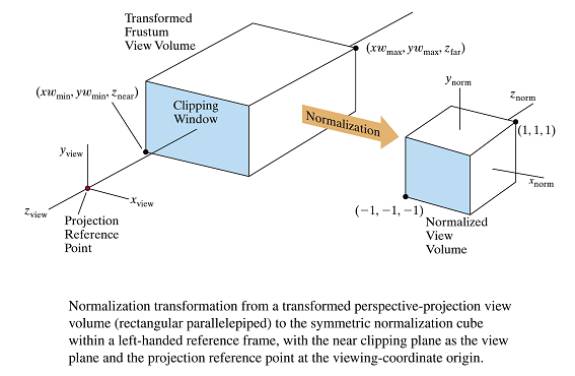
- The perspective equations map the symmetric
frustum into a parallelepiped view volume
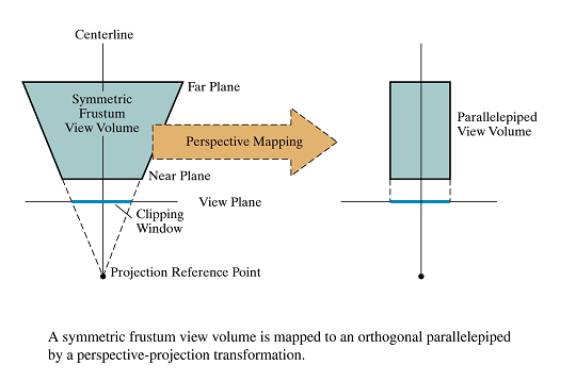
Normalized Perspective Projection View Coordfinates
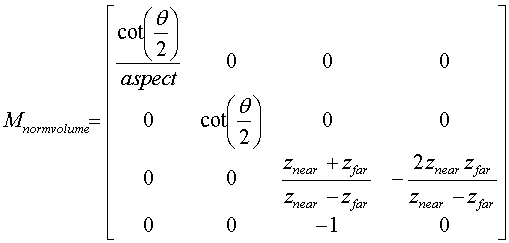
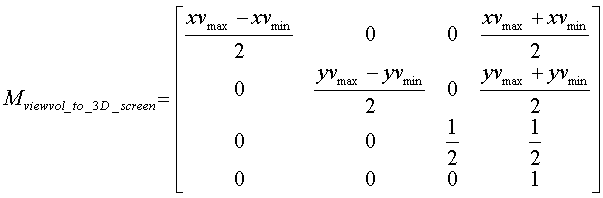
Three Dimensional Clipping
3D Clipping Planes for Symmetric Cube :