Computer Graphics
|
H&B Chapter 9 –
Visible-Surface Detection Methods
|
9.1 Classification of Visible-Surface Detection Algorithms
- Object-space methods
- Image-space methods
9.2 Back-Face Detection
·
Object space algorithm:
Back-Face removal
·
No faces on the back of
the object are displayed.
·
In general - about half
of objects faces are back faces
·
Algorithm will remove
about half of the total polygons in the image.
NOTE: Right Handed coordinate System
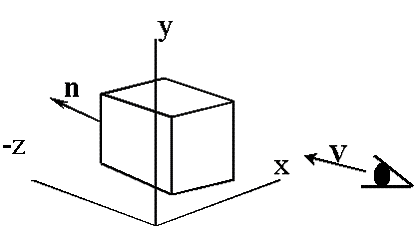
If
n·V > 0 then
polygon is backface
n·V
= |n| |V| cos q
cos
q =
n·V /
(|n| |V|)
where
|n| and |V| are the magnitudes of the vector
|V|
= sqrt( Vx2
+ Vy2
+ Vz2
)
|
Determining Surface Normal |
|||
|
|
x |
y |
z |
|
1 |
0.750 |
0.250 |
0.000 |
|
2 |
0.250 |
0.750 |
0.000 |
|
3 |
0.125 |
0.750 |
0.217 |
|
4 |
0.375 |
0.250 |
0.650 |
|
|
center |
0.438 |
0.500 |
0.108 |
|
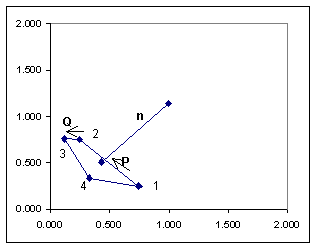
Point 2 - 1 |
P |
-0.500 |
0.500 |
0.000 |
|
Point 3 - 2 |
Q |
-0.125 |
0.000 |
0.217 |
|
Magnitude of P |
|P| |
0.7071 |
|
|
|
Magnitude of Q |
|Q| |
0.2500 |
|
|
|
|
P(Norm) |
-0.7071 |
0.7071 |
0.0000 |
|
|
Q(Norm) |
-0.5000 |
0.0000 |
0.8660 |
|
|
Normal Vector |
nx |
ny |
nz |
|
|
CrossProd (PxQ) |
0.1083 |
0.1083 |
0.0625 |
|
|
n(Norm) |
0.6547 |
0.6547 |
0.3780 |
|
cos RQ |
0.00 |
cos RP |
0.00 |
|
|n| |
0.165359 |
L(n) |
1 |
|
RlS = (RxSx+RySy+RzSz)=|R||S|cosθ |
|||
|
|
|
|
|
|
R=PxQ |
|
|
|
Rx = PyQz - PzQy
|
|
|
|
|
Ry
= PzQx -PxQz |
|
|
|
|
Rz
= PxQy - PyQx |
|
|
|
|
Standard equation of a
plane in 3 space : Ax + By + Cz + D =
0 Normal to the plane is the vector (A,B,C). |
|
Given three points in space (x1,y1,z1), (x2,y2,z2), (x3,y3,z3) the equation of the plane through these points is given by
Ax1 + By1 + Cz1 + D =
0
Ax2 + By2 + Cz2 + D =
0
Ax3 + By3 + Cz3 + D =
0
in
counter-clockwise order, and solving for
A’xk
+ B’yk + C’zk = 1
where
k = 1,2.3
A’ = -(A/D),
B’ = -(B/D), and C’ = -(C/D)
Use Cramer’s rule for solving simultaneous equations:
Begin with a system of linear equations, for example, a system involving three variables -
A’x1 + B’y1 + C’z1 = 1
A’x2 + B’y2 + C’z2 = 1
A’x3 + B’y3 + C’z3 = 1
that may be expressed in matrix form as
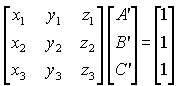
Here the coordinates constitute a coefficient matrix (A) and the vector components (A’,B’,C’) are the unknowns.
Generally, this is written as
a11x + a12 y = c1
a21x + a22 y = c2
for the 2D case and expressed in matrix form

the square matrix A, with real number entries,

can be expressed by a real number called the determinant of the matrix.
The determinant is written as -
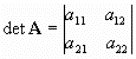 and is defined by det A = a11a22 -
a12a22
and is defined by det A = a11a22 -
a12a22
There are two other matrices obtained by replacing the coefficients in each column by the constants c1 and c2 respectively
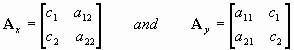
Their determinants are det Ax and det Ay respectively.
For a 3 x 3 matrix of coefficients the determinant may be expressed as either:
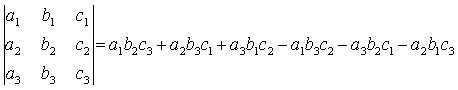
or as a cofactor expansion
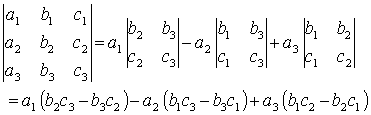
Cramer's Rule states that
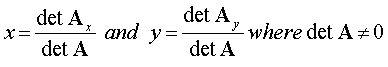
For our system, the result
is
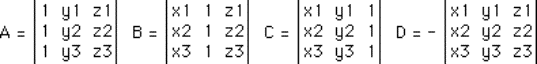
Expanding the above gives
A
= y1 (z2 - z3) + y2 (z3 - z1) + y3 (z1 - z2)
B = z1 (x2 - x3) + z2 (x3 - x1) + z3 (x1 - x2)
C = x1 (y2 - y3) + x2 (y3 - y1) + x3 (y1 - y2)
D = -x1 (y2 z3 - y3 z2) - x2 (y3 z1 - y1 z3) - x3 (y1 z2 - y2 z1)
If the 3 points are collinear then the normal (A,B,C) will be (0,0,0).
The sign of S = Ax + By + Cz + D determines which side the point (x,y,z) lies with respect to the plane.
· If s > 0 then the point lies on the same side as the normal (A,B,C).
· If s < 0 then it lies on the opposite side
· If s = 0 then the point (x,y,z) lies on the plane.
|
Calculating Normal using plane equations |
||||
|
|
|
X |
y |
z |
|
Original Data |
1 |
0.750 |
0.250 |
0.000 |
|
|
2 |
0.250 |
0.750 |
0.000 |
|
|
3 |
0.125 |
0.750 |
0.217 |
|
|
4 |
0.375 |
0.250 |
0.650 |
|
|
|
|
|
|
|
use 3 points in succession |
|
|
||
|
|
A |
0.1083 |
|
|
|
|
B |
0.1083 |
|
|
|
|
C |
0.0625 |
|
|
|
|
D |
-0.1083 |
|
|
|
|
S |
0.171 |
|
|
Same as with normal vector
Back-Face detection Procedure
![]()
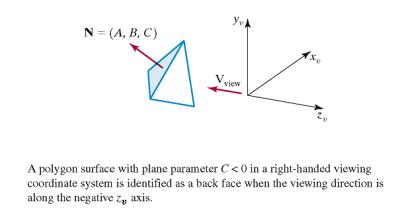
Limitations:
- Used only for solid objects modeled as a polygon mesh.
- Problematic for concave polyhedra.
e.g. partially
hidden face will not be eliminated by Back-face removal.

9.3 Depth-Buffer Method
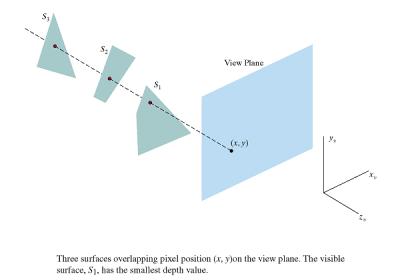
·
Image-Space Algorithm
also known as z-buffer method
· Test z - depth of each surface to determine the
surface closest to observer.
o Declare an array z buffer(x, y) with one entry for
each pixel position.
o Initialize array to the maximum depth.
o The algorithm is:
for each polygon P for each pixel (x, y) in P compute z_depth at x, y if z_depth < z_buffer (x, y) then set_pixel (x, y, color) z_buffer (x, y) <= z_depth
·
Polygon scan-conversion
procedure is modified to add the z-buffer test.
- At a surface position (x,y) the depth is calculated
from the plane equation:
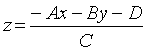
-
the depth of the next
position z’ becomes, for each successive position along scanline:
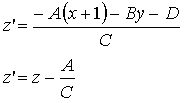
note: A/C is a constant, so successive z values are
only an addition
Possible algorithm:
1.
Begin at top vertex of
polygon
2.
Recursively calculate
x-coordinate values down left edge of polygon
3.
Subsequent x-values for
each scanline calculated from starting x-value

and depth values become
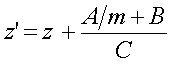
·
Advantage
Always works and is simple to implement => used in
hardware
· Disadvantages
o
Large
memory requirements
o
E.g. (640 x
480 )
§
real (4 bytes):
4bytes/pixel = 1,228,000 bytes.
§
usually use
a 24-bit z-buffer = 900,000 bytes
§
may need
additional z - buffers for special effects, e.g. shadows.
9.4 A-Buffer Method
·
Extension of z-buffer
-> accumulation buffer
·
Each buffer position
can reference a linked-list of surfaces
·
Allows pixel color to
be computed as combination of surface colors for transparency, anti-aliasing,
etc.
·
Each position has 2
fields:
1.
depth field – real
number
2.
surface data field
If depth field >= 0
depth at pixel location stored
Surface color and pixel coverage
else
(multiple
surface contributions to pixel color)
surface
color filed contains pointer to linked list of surface data comprising:
·
RGB intensity
components
·
Opacity parameter
·
Depth
·
Percent of area
coverage
·
Surface identifier
·
Other surface rendering
parameters
9.6 Depth Sorting Methods
Painter's Algorithm
·
Based on depth sorting
·
Object space algorithm
- Sort all polygons according to z value
Simplest to use maximum z value
- Draw polygons from back (maximum z) to front
(minimum z)
·
Problems with simple
Painter's algorithm:
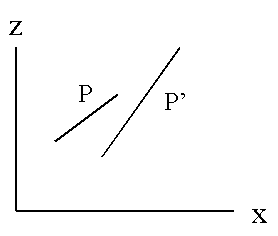
·
P’ has a
greater depth than P
·
P’ will be
drawn first.
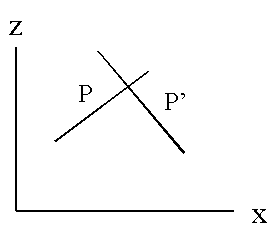
·
P’ and P
intersect
9.7 BSP-Tree Method
·
A binary space partitioning tree (bsp–tree) is a binary tree whose nodes contain
polygons.
·
Binary space
partitioning, or BSP, divides space into distinct sections by building a tree
representing that space.
·
Used to sort polygons.
·
A BSP takes the
polygons and divides them into two groups bychoosing a plane, usually taken
from the set of polygons, and divides the world into two spaces.
·
It decides which side
of the plane each polygon is on, or it may also be on the plane.
·
If a polygon intersects
the splitting plane it must be split into two separate polygons, one on each
side of the plane.
·
The tree is built by
choosing a partitioning plane and dividing the remaining polygons into two or
three lists: Front, Back and On lists – done by comparing the normal vector of
the plane with that of each polygon.
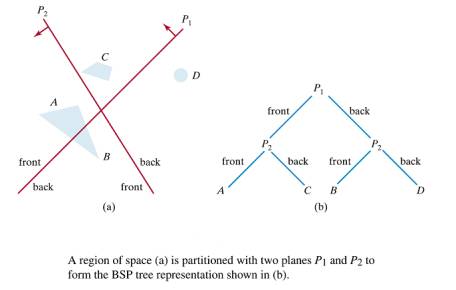
·
For each node in
a bsp-tree the polygons in the left subtree lie behind the polygon at the node
while the polygons in the right subtree lie in front of the polygon at the
node.
·
Each polygon has
a fixed normal vector, and front and back are measured relative to this fixed
normal.
·
Once a bsp-tree
is constructed for a scene, the polygons are rendered by an in order traversal
of the bsp-tree.
·
Recursive
algorithms for generating a bsp-tree and then using the bsp-tree to render a
scene are presented below.
Algorithm for Generating a BSP–Tree
- Select any polygon (plane) in the scene for the root.
- Partition all the other polygons in the scene to the back
(left subtree) or the front (right subtree).
- Split any polygons lying on both sides of the root (see
below).
- Build the left and right subtrees recursively.
BSP-Tree Rendering Algorithm (In order tree traversal)
If
the eye is in front of the root, then
Display
the left subtree (behind)
Display
the root
Display
the right subtree (front)
If
eye is in back of the root, then
Display
the right subtree (front)
Display
the root
Display
the left subtree (back)
9.10 Ray Casting Method
·
The ray casting
algorithm for hidden surfaces employs no special data structures.
·
A ray is fired
from the eye through each pixel on the screen in order to locate the polygon in
the scene closest to the eye.
·
The color and
intensity of this polygon is displayed at the pixel.
Ray
casting is easy to implement for polygonal models because the only calculation
required is the intersection of a line with a plane.

Ray Casting Algorithm
- Through each pixel, fire a ray to the eye:
- Intersect the ray with each polygonal plane.
- Reject intersections that lie outside the polygon.
- Accept the closest remaining intersection -- that is, the
intersection with the smallest value of the parameter along the line.
- The main advantage of the ray casting algorithm for hidden
surfaces is that ray casting can be used even with non-polygonal surfaces.
- All that is needed to implement the ray casting algorithm for
hidden surfaces is a line/surface intersection algorithm for each distinct
surface type.
- The main disadvantage of ray casting is that the method is
slow. Ray casting is a brute force technique that makes no use of pixel
coherence.