|
Image Creation and Graphic Primitives |
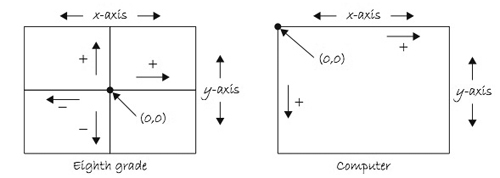
Coordinate Systems
· Object Space Coordinates given in units that define an object in its environmen t(e.g. feet, inches, angstroms, nanometers, parsecs)
· Image Space Coordinates given in pixel positions
· Normalized
· Absolute
· Relative
Processing Image Space
Coordinates.
· All shapes drawn to the screen have a position that is specified as a coordinate.
· All coordinates are measured as the distance from the origin in units of pixels.
· The origin [0, 0] is the coordinate is in the upper left of the window and the coordinate in the lower right is [width-1, height-1].
Points and Lines
Processing.org Points and Lines
|
|
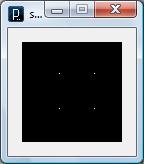
/** * Points and
Lines. * * Constructing a
simple dimensional form with lines and rectangles. * Changing the
value of the variable 'd' scales the image. * The four
variables set the positions based on the value of 'd'.
*/ int d = 40; int p1 = d; int p2 = p1+d; int p3 = p2+d; int p4 = p3+d; size(200, 200); background(0); // Draw gray box stroke(153); line(p3, p3, p2,
p3); line(p2, p3, p2,
p2); line(p2, p2, p3,
p2); line(p3, p2, p3,
p3); // Draw white points stroke(255); point(p1, p1); point(p1, p3); point(p2, p4); point(p3, p1); point(p4, p2); point(p4, p4); |
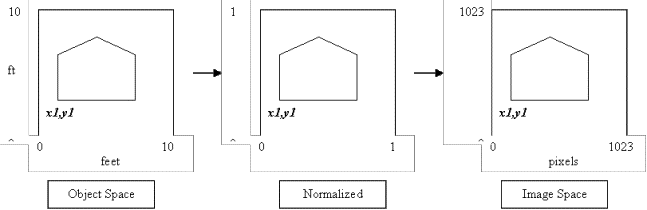
Object Space to Image Space Transformations
1. Set up coordinate system and frame of reference in object space (the space in which the real data is found)
2. Get the x,y coordinates of each point
3. Normalize each coordinate to between 0 and 1 by dividing the coordinate by the width or height of the reference frame
4. Scale the normalized value by the width or height of the drawing area.
e.g.
Line Drawing Algorithms
· Slope-intercept equation -> y = mx + b
· Use line segments -> (x1,y1) (x2,y2)
Slope = m = (y2 y1)/(x2 x1)
y= [(y2-y1)/(x2-x1)]m +b
· solve for b assuming x1,y1
b = y1 m x1
· Straight line algorithms based on line equation
o For every interval in x -> Dx, we can compute Dy
o Slope = m = Dy / Dx to give
Dy = m Dx
Dx = Dy / m
· For vector displays Dx, Dy can be set to deflection voltages
o For | m | < 1 set Dx to constant
Dy = m Dx
o For | m | > 1 set Dy to constant
Dx = Dy / m
Processing Example
|
|
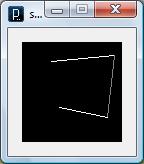
void setup() { size(200, 200); background(0); stroke(255); noFill(); noLoop(); } int x0 = 20; int y0
= 40; int x1=150; int
y1=175; void draw() { int dx = x1 - x0; int dy = y1 - y0; point(x0, y0); if (abs(dx) > abs(dy)) { // slope
< 1 float m = (float) dy
/ (float) dx; // compute slope float b = y0 - m*x0; dx
= (dx < 0) ? -1 : 1; while (x0 != x1) { x0 += dx; point(x0, round(m*x0 + b)); } } else if (dy != 0) { // slope >= 1 float m = float(dx)/float(dy); // compute slope float b = x0 - m*y0; dy
= (dy < 0) ? -1 : 1; while (y0 != y1) { y0 += dy; point(round(m*y0 + b), y0); } } } |
DDA Line drawing Algorithm
· General scan conversion problem: which pixels to turn on
o
Assume a line with positive slope in the first
octant, i.e., 0.0 <= m <= 1.0.
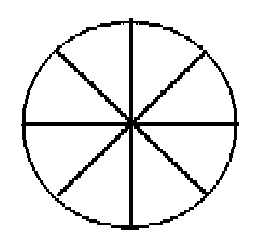
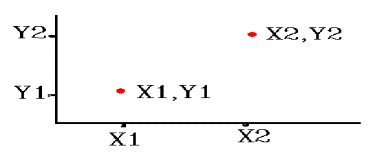
o
Drawn from left to right: (X1, Y1) to (X2, Y2):
o Problem: as xi is incremented to xi+1, which pixel gets turned on - xi+1, yi or xi+1, yi+1?
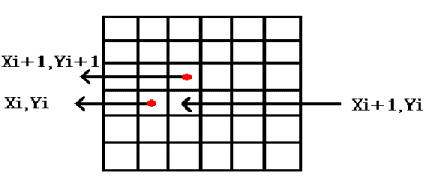
Digital Differential Analyzer
· Based on calculating Dx or Dy
· Sample line in unit intervals in one direction and calculate increment in other
o Unit steps are always along the coordinate of greatest change
§ e.g. if Dx = 10 and Dy = 5, then take unit steps along x and compute steps along y.
§ Assume a line of positive slope from x1, y1 to x2, y2.
if m <= 1.0 then
let x_step = 1 {dx = 1, dy = 0 or 1}
else {m > 1.0}
let y_step = 1 {dy = 1, x_step = 0 or 1 }
Note: {slope = m = dy/dx}
{m <= 1.0} for x_step = 1, dy = m = yi+1 - yi -> yi+1 = yi + m
{m > 1} for y_step = 1 m = 1/dx => dx = 1/m => xi+1 = xi + 1/m
If, instead, we draw from x2 ,y2 to x1,y1 then:
a.) dx = -1 yi+1 = yi -m or
b.) dy = -1 xi+1 = xi - 1/m
§ For a line with slope < 0.0 and drawing from x1,y1 to x2,y2, i.e., left to right then:
if |m| < 1 then
let dx = 1 and yi+1 = yi + m
else {|m| ³ 1}
let dy = -1 and xi+1 = xi -1/m
if draw from x2, y2 to x1, y1 (right to left) then:
if |m| < 1 then let dx = -1 yi+1 = yi -m
else {|m| ³ 1} dy = 1 xi+1 = xi + 1/m
§ Complete DDA Algorithm
procedure DDA( x1, y1, x2, y2: integer);
var
dx, dy, steps: integer;
x_inc, y_inc, x, y: real;
begindx := x2 - x1; dy := y2 - y1;
if abs(dx) > abs(dy) then
steps := abs(dx); {steps is larger of dx, dy}
elsesteps := abs(dy);
x_inc := dx/steps; y_inc := dy/steps;
{either x_inc or y_inc = 1.0, the other is the slope}x:=x1; y:=y1;
set_pixel(round(x), round(y));
for i := 1 to steps do
beginx := x + x_inc;
y := y + y_inc;
set_pixel(round(x), round(y));
end;
end; {DDA}
§ Example
|
DDA algorithm calculation |
|
|
|
|
|
|
|
|
|
|
|
||||
|
xa |
ya |
xb |
yb |
dx |
dy |
step |
xinc |
yinc |
|
|
|
|
|
|
|
|
2 |
0 |
10 |
5 |
8 |
5 |
8 |
1.000 |
0.625 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
step |
x |
y |
xs |
ys |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
0 |
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3.000 |
0.63 |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4.000 |
1.25 |
4 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
5.000 |
1.88 |
5 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
6.000 |
2.5 |
6 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
7.000 |
3.13 |
7 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
8.000 |
3.75 |
8 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
9.000 |
4.38 |
9 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
10.000 |
5 |
10 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§ Problems / Concerns:
o Round-off error
o FP calculation time
Processing
DDA Algorithm
|
|
void setup() { size(200, 200); background(0); stroke(255); noFill(); noLoop(); } int x0 = 0; int y0 =
0; int x1=150; int
y1=175; void draw() { int dx = x1 - x0; int dy = y1 - y0; float t = 0.5; point(x0, y0); if (abs(dx) > abs(dy)) { // slope
< 1 float m = (float) dy
/ (float) dx; // compute slope t+= y0; dx
= (dx < 0) ? -1 : 1; m*=dx; while (x0 != x1) { x0 += dx; t +=m; point(x0, int(t)); } } else if (dy != 0) { //
slope >= 1 float m = float(dx)/float(dy); // compute slope t += x0; dy
= (dy < 0) ? -1 : 1; m *=dy; while (y0 != y1) { y0 += dy; t+= m; point(int(t),
y0); } } } |
Bresenham (Decision Variable) Method
§ Use incremental integer calculations
§ Makes decision of which is next pixel to turn on
§ Look at the center of the pixels
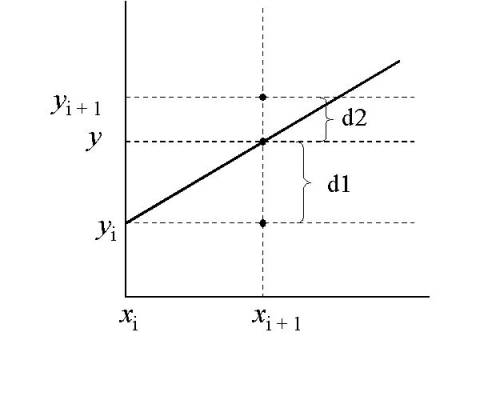
§ Determine d1 and d2 -> the "error", i.e., the difference from the " true line."
§ d1 and d2 specify an integer parameter whose value is proportional to separation of two pixels
§ Steps in the Bresenham algorithm:
1. Determine the error terms
2. Define a relative error term such that the sign of this term tells which pixel to choose
3. Derive equation to compute successive error terms from first
4. Compute first error term
§ Example | m| < 1
o Sample x at unit intervals
o Start at (x0,y0) and move to (x1, ?)
o Must find y closest to line path
o y is coordinate of true line at xi+1
y = m(xi+1) + b
d1 = y - yi = m(xi+1) + b yi
d2 = (yi+1) - y = yi+1 -m(xi+1) - b
then d1 - d2 = 2m(xi+1) - 2y + 2b -1
§ now define pi = dx(d1 - d2) = relative error of the two pixels.
§ note: pi < 0 if yi pixel is closer
pi >= 0 if yi+1 pixel is closer
( = 0 is our choice).
§ Therefore we only need to know the sign of pi .
§ With m = dy/dx and substituting in for (d1 - d2) we get
(1) pi = 2 * dy * xi - 2 * dx * yi + 2 * dy + dx * (2 * b - 1)
§ let C = 2 * dy + dx * (2 * b - 1)
· Now look at the relation of p's for successive x terms.
o pi+1 = 2dy
* xi+1 - 2 * dx * y i+1 + C
o pi+1 - pi = 2 * dy * (xi+1 - xi) - 2 * dx * ( yi+1 - yi)
with xi+1 = xi + 1 and yi+1= yi + 1 or yi
(2) pi+1 = pi + 2 * dy - 2 * dx(yi+1 -yi)
Note: b = y - dy / dx * x
· Now compute p1 (x1,y1) from (1)
p1 = 2dy * x1 - 2dx * y1 + 2dy + dx(2y1 - 2dy / dx * x1 - 1)
= 2dy * x1 - 2dx * y1 + 2dy + 2dx * y1 -
2dyx1 - dx
= 2dy - dx
· if pi < 0 choose yi and pi+1 = pi + 2dy
· else {pi >= 0} and choose yi+1 so pi+1 = pi + 2dy - 2dx
Bresenham Algorithm for 1st octant:
1. Enter endpoints (x1, y1) and (x2, y2).
2. Display x1, y1.
3. Compute dx = x2 - x1 ; dy = y2 - y1 ; p1 = 2dy - dx.
4. If p1 < 0.0, display (x1 + 1, y1), else display(x1+1, y1 + 1)
5. if p1 < 0.0, p2 = p1 + 2dy else p2 = p1 + 2dy - 2dx
6. Repeat steps 4, 5 until reach (x2, y2).
Note: Only integer Addition and Multiplication by 2. Notice we always increment x by 1.

For a generalized Bresenham Algorithm must look at behavior in different octants.
Worked Example
|
Bresenham |
|
|
|
|
|
|
|
|
||
|
xa |
ya |
xb |
yb |
dx |
dy |
2dx |
2dy |
2dy-2dx |
|
|
|
20 |
10 |
30 |
18 |
10 |
8 |
20 |
16 |
-4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
pi |
xi+1 |
yi+1 |
|
|
|
|
|
|
|
|
|
|
20 |
10 |
|
|
|
|
|
|
|
|
0 |
6 |
21 |
11 |
|
|
|
|
|
|
|
|
1 |
2 |
22 |
12 |
|
|
|
|
|
|
|
|
2 |
-2 |
23 |
12 |
|
|
|
|
|
|
|
|
3 |
14 |
24 |
13 |
|
|
|
|
|
|
|
|
4 |
10 |
25 |
14 |
|
|
|
|
|
|
|
|
5 |
6 |
26 |
15 |
|
|
|
|
|
|
|
|
6 |
2 |
27 |
16 |
|
|
|
|
|
|
|
|
7 |
-2 |
28 |
16 |
|
|
|
|
|
|
|
|
8 |
14 |
29 |
17 |
|
|
|
|
|
|
|
|
9 |
10 |
30 |
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Applet example of DDA and Bresenham
Geometric Primitives
Points
P1 (x1, y1, z1)
Processing Example
point(x, y)
point(x, y, z)
Parameters
|
x |
int or float: x-coordinate of the point |
|
y |
int or float: y-coordinate of the point |
|
z |
int or float: z-coordinate of the point |
|
|
size(100, 100,
P3D); background(0); stroke(255); point(30, 20,
-50); point(85, 20,
-50); point(85, 75,
-50); point(30, 75, -50); |
Line Segments: Two endpoints
P1 (x1, y1, z1) -> P2 (x2, y2, z2)
Processing Example
Syntax
line(x1, y1, x2, y2)
line(x1, y1, z1, x2, y2, z2)
|
x1 |
int or float: x-coordinate of the first point |
|
y1 |
int or float: y-coordinate of the first point |
|
z1 |
int or float: z-coordinate of the first point |
|
x2 |
int or float: x-coordinate of the second point |
|
y2 |
int or float: y-coordinate of the second point |
|
z2 |
int or float: z-coordinate of the second point |
|
|
size(100, 100,
P3D); background(0); stroke(255); line(30, 20, 0,
85, 20, 15); stroke(126); line(85, 20, 15,
85, 75, 0); stroke(255); line(85, 75, 0, 30, 75, -50); |
Polyline
Connected line segments
Processing Example
There is no formal Polyline function in Processing. Can use Shape primitive
· beginShape() and endShape() functions allow creating more complex forms.
· beginShape() begins recording vertices for a shape and endShape() stops recording.
· The value of the MODE parameter tells it which types of shapes to create from the provided vertices.
· With no mode specified, the shape can be any irregular polygon.
·
Complex
shapes may be created by including programming logic within functions
|
|
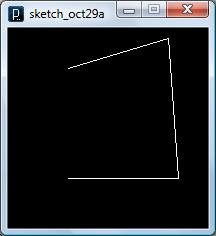
size(200, 200); background(0); stroke(255); noFill(); beginShape(); vertex(60, 40); vertex(160, 10); vertex(170, 150); vertex(60, 150); endShape(); |
Polygons
Closed polyline where initial and terminal points coincide.
Processing Example Uses Shape()
function
|
|
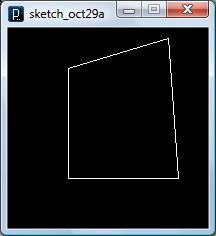
size(200, 200); background(0); stroke(255); noFill(); beginShape(); vertex(60, 40); vertex(160, 10); vertex(170, 150); vertex(60, 150); endShape(CLOSE); |
Wireframe models
· Consist of vertices, edges, and polygons (e.g. cube)
· Stored as vertex list, edge listing, polygon listing
Polyhedron
· Closed polygon net
· Encloses a definite volume
· Polygons are faces of volume
· e.g. Platonic solids
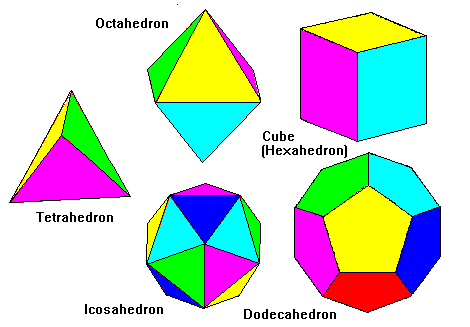
Name |
n |
m |
f |
v |
e |
|
tetrahedron |
3 |
3 |
4 |
4 |
6 |
|
hexahedron |
4 |
3 |
6 |
8 |
12 |
|
octahedron |
3 |
4 |
8 |
6 |
12 |
|
dodecahedron |
5 |
3 |
12 |
20 |
30 |
|
icosahedron |
3 |
5 |
20 |
12 |
30 |
|
f,v,e: Faces, Vertices, Edges |
|||||
See Also Visual Geometry Pages
· Problem with polyhedra takes many polyhedra to approximate smooth surface
Curved Surfaces
· Used for realistic models
· Uses small surface patches instead of polyhedra
·
Uses
solid modeling from prototype sphere, cone, cylinder, polyhedra
=> Constructive Solid Geometry (
Parametric Curves
· A point P(u) on a curve depends on a parameter u.
· Since P(u) also depends on an x coordinate and y coordinate, x and y are functions of u with
P(u) = [ x(u) y(u) ]
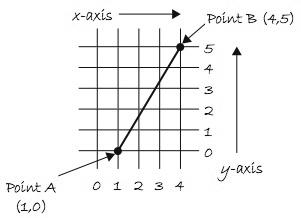
· A parametric representation of a straight line is then
P(u) = P1 + ( P2 - P1 ) u where
x(u) = x1 + ( x2 - x1 ) u 0 <= u <= 1
y(u) = y1 + ( y2 - y1 ) u 0 <= u <= 1
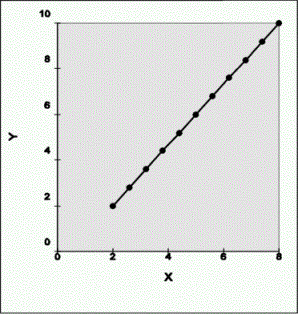
· e.g. line from P1 (2,2) to P2 (8, 10)
Parametric Equation For Straight Line
from P1 (2,2) to P2(8,10)
|
u |
x(u) |
y(u) |
|
0.0 |
2.0 |
2.0 |
|
0.1 |
2.6 |
2.8 |
|
0.2 |
3.2 |
3.6 |
|
0.3 |
3.8 |
4.4 |
|
0.4 |
4.4 |
5.2 |
|
0.5 |
5.0 |
6.0 |
|
0.6 |
5.6 |
6.8 |
|
0.7 |
6.2 |
7.6 |
|
0.8 |
6.8 |
8.4 |
|
0.9 |
7.4 |
9.2 |
|
1.0 |
8.0 |
10.0 |
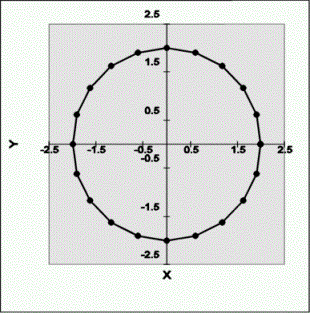
· e.g. Circle
x(u) = r cos (2 p u)
y(u) = r sin (2 p u)
o Unit circle varying u in increments of 0.05 from 0 to 1.
o Beginning with P1 (1,0) on the x axis, the circle is built by counterclockwise rotation of point P1 in 2pu (360 degrees u) increments
Parametric Equation For Circle of Radius 2.0
|
u |
x(u) |
y(u) |
|
0.00 |
2.00 |
0.00 |
|
0.05 |
1.90 |
0.62 |
|
0.10 |
1.62 |
1.18 |
|
0.15 |
1.18 |
1.62 |
|
0.20 |
0.62 |
1.90 |
|
0.25 |
0.00 |
2.00 |
|
0.30 |
-0.62 |
1.90 |
|
0.35 |
-1.18 |
1.62 |
|
0.40 |
-1.62 |
1.18 |
|
0.45 |
-1.90 |
0.62 |
|
0.50 |
-2.00 |
0.00 |
|
0.55 |
-1.90 |
-0.62 |
|
0.60 |
-1.62 |
-1.18 |
|
0.65 |
-1.18 |
-1.62 |
|
0.70 |
-0.62 |
-1.90 |
|
0.75 |
0.00 |
-2.00 |
|
0.80 |
0.62 |
-1.90 |
|
0.85 |
1.18 |
-1.62 |
|
0.90 |
1.62 |
-1.18 |
|
0.95 |
1.90 |
-0.62 |
|
1.00 |
2.00 |
0.00 |
|
|
|
|
Curve Design
· Given n + 1 points => find curve which fits shape
· Interpolation
· Approximation
· Try modeling curves using segments
+> use linear combination of basis functions
![]()
· Usually use polynomials => easy to use
· Polynomials of degree n
![]()
· Continuous piecewise polynomial Q(x) of degree n is a set of k polynomials q(x), each of degree n and k+1 knots (nodes) t0, , tk ,such that
Q(x) = qi(x) for all ti <=
x <= ti+1 for i = 0,
, k-1
· Polynomials must match or piece together at knots, so
qi-1(tI ) = qi-1(ti),
i = 0,
, k-1
· Most useful polynomials are cubic (n =3)
Common Basis Functions
· e.g. Bezier Curve
· Bιzier curve is a polynomial curve the shape of which is determined by the placement of a series of control points.
· Figure displays a series of Bιzier
curves with four control points.
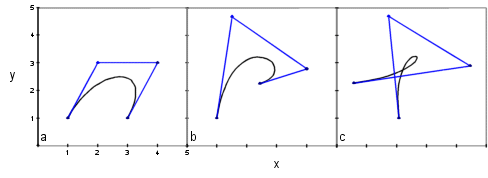
· Curves begin with a definition of P(u) as
![]() 0 <= u = 1
0 <= u = 1


· Bi are the control points
· Jn,i are the basis or blending functions which assure the curve travels smoothly from B0 to B3 .
· Four vertices define a cubic equation with four blending functions.
· This gives
J3,0 (u) = ( 1 - u )3
J3,1 (u) = 3 u ( 1 - u )2
J3,2 (u) = 3 u2 ( 1 - u )
J3,3 (u) = u3
· P(u) becomes
P(u) = B0 ( 1 - u )3 + B1 (3 u ( 1 - u )2 ) + B2 (3 u2 ( 1 - u )) + B3 u3
· x(u) and y(u) are calculated by substituting in the x and y coordinates of B0 through B3, respectively.
· Values for u are selected in a uniform way.
· Figure was calculated with B0 = (1,1), B1 = (2,3), B2 = (4,3), and B3 = (3,1) and varying u from 0 to 1 in 0.05 increments
Bιzier Curve for
B0(1,1), B1(2,3), B2(4,3), B3(3,1)
|
u |
P(x) |
P(y) |
|
0.00 |
1.00 |
1.00 |
|
0.05 |
1.16 |
1.29 |
|
0.10 |
1.33 |
1.54 |
|
0.15 |
1.50 |
1.77 |
|
0.20 |
1.69 |
1.96 |
|
0.25 |
1.88 |
2.13 |
|
0.30 |
2.06 |
2.26 |
|
0.35 |
2.25 |
2.37 |
|
0.40 |
2.42 |
2.44 |
|
0.45 |
2.59 |
2.49 |
|
0.50 |
2.75 |
2.50 |
|
0.55 |
2.89 |
2.49 |
|
0.60 |
3.02 |
2.44 |
|
0.65 |
3.12 |
2.37 |
|
0.70 |
3.20 |
2.26 |
|
0.75 |
3.25 |
2.13 |
|
0.80 |
3.27 |
1.96 |
|
0.85 |
3.26 |
1.77 |
|
0.90 |
3.21 |
1.54 |
|
0.95 |
3.13 |
1.29 |
|
1.00 |
3.00 |
1.00 |
Processing Bezier Curves
· Curves are defined by a series of anchor and control points.
· The first two parameters specify the first anchor point and the last two parameters specify the other anchor point.
·
The
middle parameters specify the control points which define the shape of the
curve.
|
|
size(200, 200); background(0); noFill(); stroke(255, 255,
0); line(30, 20, 160,
5); line(80, 150, 30,
75); stroke(255); bezier(30, 20, 160, 5, 80, 150, 30, 75); |
Quadric Surfaces
· Sphere
![]()
Parametric form:

· Ellipsoid
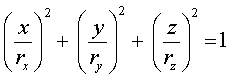
Parametric form:

See also Visual Geometry pages
· Torus

See also Visual Geometry page
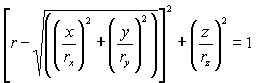
Parametric Form:
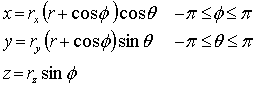
· Superquadrics
o
Super ellipse

o s = parameter
o Parametric
equations:
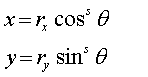

o
Super ellipsoid
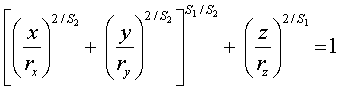
Parametric equation:
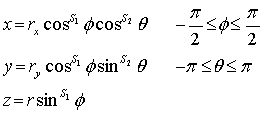

Pixel Addressing and Object Geometry
Object Description:
o World description
o precise coordinate positions
o infinitesimally small mathematical points
o Pixel Coordinates
o Finite screen areas
Aligning Approaches
1. Adjust dimensions of displayed objects to account for amount of overlap of pixel areas with object boundaries
2. Map world coordinates onto screen positions between pixels to align object boundaries with pixel boundaries instead of centers
Screen Grid Coordinates
o Use horizontal/vertical pixel boundary lines instead of centers
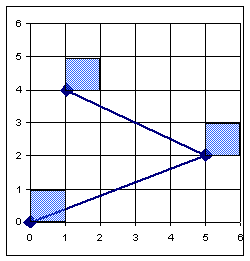
Old Way -Pixels are line intersections New Way -Pixels are areas
Maintaining Geometric Properties of Displayed Objects
· Geometric objects are transformed into pixels
· Must account for finite size when transformed to screen
· Say, we have a line from (20,10)
to (30,18)

· Line precisely ends in real world at (30,18)
· Pixel extends beyond line
· Must plot pixels from (20,10) to (29,17) to remain on interior
· Same is true for Rectangle
· Vertices at (0,0), (4,0),
(4,3), (0,3)
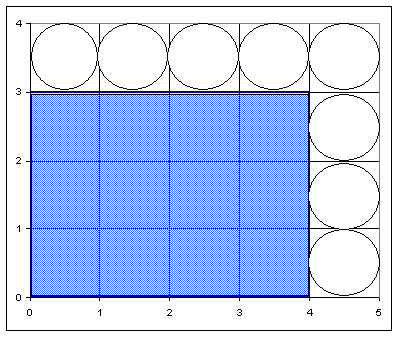
Polygon
· A plane figure specified by a set of three or more coordinate positions, called vertices, that are connected in sequence by straight-line segments called the edges or sides of the polygon.
· In basic geometry, the polygon edges must have no common point other than their endpoints.
· A polygon must have all its vertices within a single plane and there can be no edge crossings.
·
Convex polygon all interior angles of a polygon are less than or equal to 180 degrees.
Concave polygon
· at least one interior angles of a polygon is greater than 180 degrees.
· extension of some edges of a concave polygon will intersect other edges
· somepair of interior points will produce a line segment that intersects the polygon boundary
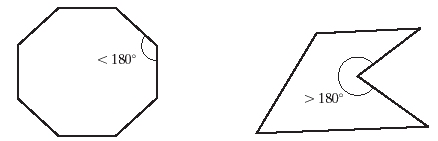
Concave Polygon identification algorithm
· Set up a vector for each polygon edge
· Use the cross product of adjacent edges to test for concavity.
o All vector products will be of the same sign (positive or negative) for a convex polygon.
o If z value of some cross products is positive while others are negative, concave polygon exits.
(assume no three successive vertices are collinear => gives 0 crossproduct)
Example:
z-component processing

(E1 X E2) > 0
(E2 X E3) > 0
(E3 X E4) < 0
(E4 X E5) > 0
(E5 X E6) > 0
(E6 X E7) > 0
§ Cross product:
V1 X V2 = u |V1||V2| sinq
where u is unit vector perpendicular to V1 and V2
V1 X V2 = ( V1y V2z V1z V2y, V1z V2x V1x V2z, V1x V2y V1y V2x )
Splitting Concave Polygons
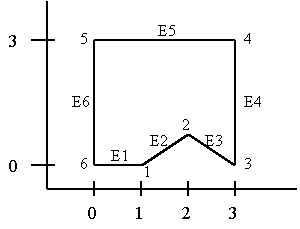
E1 = (1, 0, 0)
E2 = (1, 1, 0)
E3 = (1, -1, 0)
E4 = (0, 3, 0)
E5 = (-3, 0, 0)
E6 = (0, -3, 0)
(E1 X E2) = (0, 0,
1)
(E2 X E3) = (0, 0,
-2)
(E3 X E4) = (0, 0,
3)
(E4 X E5) = (0, 0,
9)
(E5 X E6) = (0, 0,
9)
(E6 X E1) = (0, 0,
3)
Since E2 X E3 z-value < 0 must split polygon along line E2
Must determine intersection of line with edge E4
Use slope-intercept form of line:
y = max + ba y = mbx + bb
max + ba = mbx + bb
x = ( bb - ba ) / (ma - mb )
and
x = ( y - ba ) / ma x = ( y bb ) / mb
( y - ba ) / ma = ( y bb ) / mb
y = (ma bb mb ba ) / (ma - mb )
§ Alternative method for splitting concave polygons
1. Rotational Method:
2. Proceed counterclockwise
3. Translate each polygon vertex Vk in sequence to origin
4. Rotate cloackwise so next vertex is on x axis
5. If next vector Vk+2 is below axis, polygon is concave
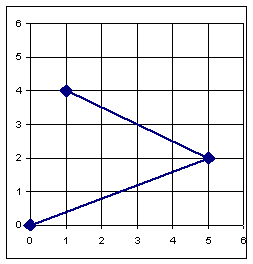
e.g.
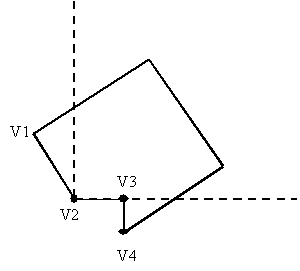
§ can fined, since (x, y=0), substitute into
x = x1 + ( y y1 ) / m
so
x = x1 - y1 / m
Polygon Tables
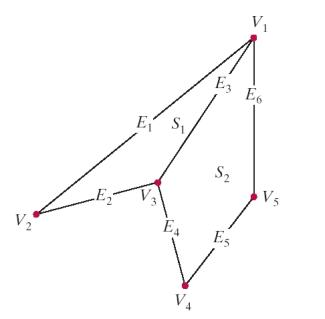
|
VERTEX TABLE |
|
V1 : x1 , y1 , z1 |
|
V2 : x2 , y2 , z2 |
|
V3 : x3 , y3 , z3 |
|
V4 : x4 , y4 , z4 |
|
V5 : x5 , y5 , z5 |
|
|
|
1 : 1 , 2 |
|
2 : 2 , 3 |
|
3 : 3 , 1 |
|
4 : 3 , 4 |
|
5 : 4 , 5 |
|
6 : 5 , 1 |
|
SURFACE-FACET TABLE |
|
S 1 : 1 , 2 , 3 |
|
S 2 : 3 , 4 , 5 , 6 |
Processing Polygon Fill-Area Functions
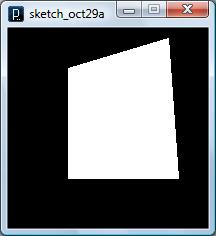
Basic Polygons: Triangle ( 2D & 3D), Rectangle (2D), and Quad(rilateral) (2D)
Use Shape() function with noFill() flag turned off for any shapes
|
size(200, 200); background(0); stroke(255); // noFill(); beginShape(); vertex(60, 40); vertex(160, 10); vertex(170, 150); vertex(60, 150); endShape(CLOSE); |
|