Computer Graphics
|
|
Illumination Models
and Surface Rendering |
Light Sources
- Point
· Infinitely Distant
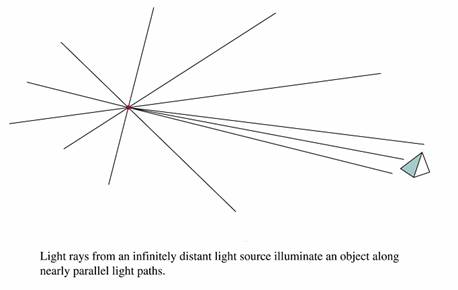
- Radial Intensity Attenuation
– (1/d2)
· Problems: Point Source with 1/d2 attenuation does not always produce realistic results.
· Produces too much intensity variation for near objects and not enough for distant.
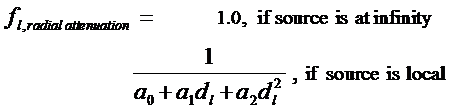
· Directional Light Sources and Spotlight effects

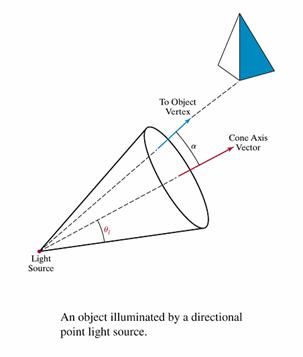
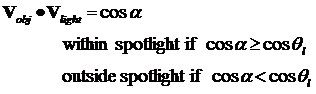
Angular Intensity Attenuation
![]()
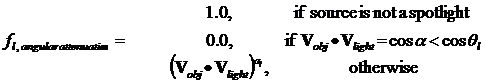
Surface Lighting Effects
· Diffuse Reflection
· Specular Reflection
· Ambient
Simple Illumination Model
Surfaces
in real world environments receive light in 3 ways:
1.
Directly from existing light
sources such as the sun or a lit candle
2.
Light that passes and refracts
through transparent objects such as water or a glass vase
3.
Light reflected, bounced, or
diffused from other exisiting surfaces in the
environment
Local Illumination
·
Material Models
- Diffuse illumination
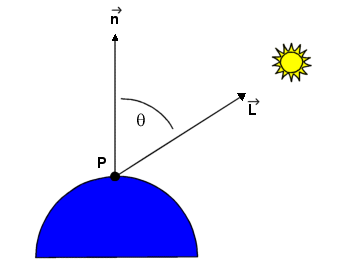
Lambert's
cosine law of reflection as shown in the above diagram:
1.
n; a normal vector to the
surface to be illuminated.
2.
L, a vector from the surface position that points
towards the light source.
3.
Il, an
intensity for a point light source.
4.
kd , a diffuse
reflection constant.
Equation gives
the brightness of a surface point in terms of the brightness of a light source
and its orientation relative to the surface normal vector, n,
![]()
·
I is the reflected intensity
Measures how bright the surface is
at that point.
·
Surface brightness varies as a
function of the angle between n and L
When n and L coincide, the
light source is directly overhead.
·
I is at a maximum and cosq = 1.
As the angle increases to 90o,
the cosine decreases the intensity to 0.
·
All the quantities in the equation
are normalized between 0 and 1.
·
I is converted
into frame buffer intensity values by multiplying by the number of shades
available.
·
With 28 = 256 possible
shades, we have 1 * 255, the brightest frame buffer intensity.
·
For n and L at an angle of
45 o, I = cos 45 o * 256 = 181.

- An
image rendered with a Lambertian shader exhibits a dull, matte finish.
- It
appears as if it has been viewed by a coal miner with a lantern attached
to his helmet.
- In
reality, an object is not only subjected to direct illumination from the
primary light source Il , but
secondary scattered light from all remaining surfaces.
- Ambient illumination
·
Simple illuminated model is unable
to directly accommodate all scattered light
·
It is grouped together as independent
intensity,
·
The formula becomes
![]()
·
Iaka is the
ambient illumination term, taking into account the additional environmental
illumination, Ia, and the
ability of the object to absorb it, ka.
·
Below Figure: Only ambient illumination

- Below Figure: Diffuse + ambient illumination

- Illumination
decreases from the light source by I/d2.
- Objects
at a greater distance from the light source receive less illumination and
appear darker.
- Above
equation is distance independent.
- Dividing
the Lambertian term by d2 would seem
to get the physics right, but it makes the intensity vary sharply over
short distance.
- Modified
distance dependence is employed, giving

·
d is the distance from the light
source to the object
- Specular
Highlights – (Phong Reflection Model)
·
Regions of significant brightness,
exhibited as spots or bands, characterize objects that specularly
reflect light.
·
Specular
highlights originate from smooth, sometimes mirrorlike
surfaces
·
Fresnel equation is
used to simulate this effect.
·
The Fresnel
equation states that for a perfectly reflecting surface the angle of incidence
equals the angle of reflection.
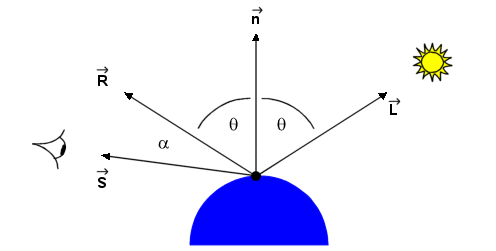
·
Most objects are not perfect
mirrors.
o some angular scattering of light.
o If the viewer increases the angle (a ) between
himself, the line of sight vector (S),
and the reflectance vector (R), the
bright spot gradually disappears.
o Smooth surfaces scatter light less then rough surfaces.
o This produces more localized highlights.
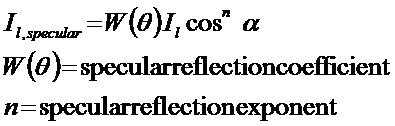

o Building this effect into the lighting model gives
![]()
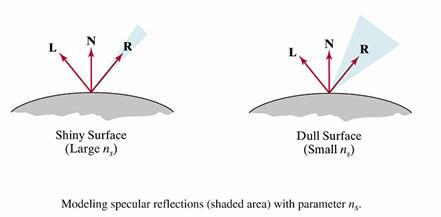
·
Specular
reflectance term possesses a specular
reflectance constant, ks.
·
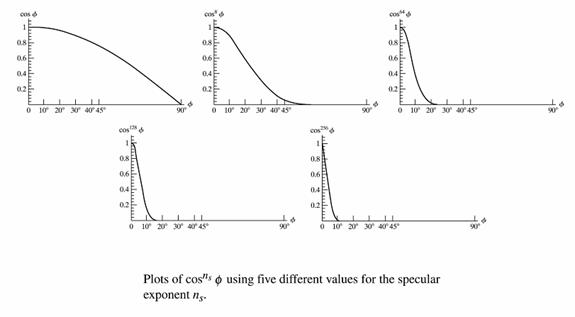
The cosine term is raised to the nth power.
o Small values of n (e.g. 5) distribute the specular
highlights, characteristic of glossy paper.
o High values of n (e.g. 50) are characteristic of metals.

1.
Simple Illumination Model
- Deficiencies
- point
light source
- no
interaction between objects
- ad
hoc, not based on model of light propagation
- Benefits
- fast
- acceptable
results
- hardware
support
How to Implement
Use the
following formula for diffuse + ambient illumination
![]() 0
£ q £ p/2
0
£ q £ p/2
1.
Determine polygon’s surface normal
2.
Calculate cosine of angle between
surface normal and illumination vector
3.
Scale to frame buffer values
between 0 and 255
1.
Determine polygon’s surface normal

i.
Begin with polygon vertices
|
|
x |
y |
z |
|
1 |
0.750 |
0.250 |
0.000 |
|
2 |
0.250 |
0.750 |
0.000 |
|
3 |
0.125 |
0.750 |
0.217 |
|
4 |
0.375 |
0.250 |
0.650 |
ii.
Create vectors P and Q
P = [ P2 – P1] = [ Px Py Pz ] = [ x2 –
x1 y2 – y1 z2 – z1 ]
= [ -0.500 0.500 0.000
]
Q = [ P3 – P2] = [ Qx Qy Qz ] = [ x2 –
x2 y3 – y2 z3 – z2 ]
= [ -0.125 0.000 0.217 ]
iii.
Determine length of P and Q
|P| = sqrt( Px2 + Py2 + Pz2 ) =
0.7071
|Q| = sqrt( Qx2 + Qy2 + Qz2 ) =
0.2500
iv.
Normalize P and Q
P(norm) = P
/ |P| = [ Px
/ |P| Py /
|P| Pz /
|P| ]
= [ -0.7071 0.7071 0.0000 ]
Q(norm) = Q
/ |Q| = [ Qx / |Q| Qy / |Q| Qz / |Q| ]
= [ -0.5000 0.0000 0.8660
]
v.
Calculate normal vector using
cross product:
|
n = PxQ |
|
|
nx = PyQz - PzQy |
|
|
ny = PzQx -PxQz |
|
|
nz = PxQy - PyQx |
|
n = [nx nx nx] = [0.1083 0.1083 0.0625]
vi.
Normalize n
|
|n| = |
0.165359 |
|
||||
|
n(Norm) = |
[0.6547 |
0.6547 |
0.3780 ] |
||
vii.
Create a light vector
·
Select a point on the polygon
surface and position for the light source
o
A polygon vertex may be selected or
a position inside the polygon.
o
Here we select a position inside
the polygon by calculating the midpoint between the 1st and 3rd
vertices
(xmid, ymid, zmid) =
( (x1 + x3)/2 , (y1 + y3)/2 , (z1 + z3)/2 )
|
= (0.438 |
0.500 |
0.108) |
o
A position for the light source is
give as
|
x |
y |
z |
|
10 |
10 |
-5 |
Note: If observer is in –z direction than z value of light is also –z.
·
Compute light vector L
|
|
|
Lx |
Ly |
Lz |
|
|
Light
Vector (L) |
9.563 |
9.500 |
-5.108 |
|
|
|L| |
14.415 |
|
|
|
|
L(Norm) |
0.66338 |
0.65905 |
-0.35438 |
2.
Calculate cosine of angle between
surface normal and illumination vector
i.
Use dot product formula:
|
nlL = (nxLx+nyLy+nzLz)=|n||L|cosq |
Since n and L are already
normalized the formula reduces to
|
nlL = (nxLx+nyLy+nzLz) = cosq |
||
|
= 0.7318 |
|
3.
Scale to frame buffer values
between 0 and 255
0.7318 * 255 = int(186.6) = 186
Polygon Rendering Methods
Flat Shading (also known as faceted shading)
Shades each polygon of an object based on the angle between
the polygon's surface normal and the direction of the light source.
Disadvantage - it gives low-polygon models a
faceted look. Sometimes this look can be advantageous though, such as in
modeling boxy objects. Artists sometimes use flat shading to look at the
polygons of a solid model they are creating.

Gouraud Shading
Gouraud shading (Henri Gouraud, 1971) is used to achieve smooth lighting on
low-polygon surfaces using the Lambertian diffuse lighting
model.
1. Calculates the surface normals for the polygons.
2. Normals are then averaged for all the polygons that meet at
each vertex to produce a vertex normal.
3. Lighting computations are then
performed to produce intensities at vertices.
4. These intensities are interpolated
along the edges of the polygons.
5. The polygon is filled by lines drawn
across it that interpolate between the previously calculated edge
intensities.
Advantage - Gouraud
shading is superior to flat shading which requires significantly less
processing than Gouraud, but gives low-polygon models
a sharp, faceted look.


Phong Shading (Phong
Interpolation Model)
·
An
improved version of Gouraud shading that provides a
better approximation to the Phong shading model.
·
Main
problem with Gouraud shading - when a specular highlight occurs near the center of a large
triangle, it will usually be missed entirely. Phong
shading fixes the problem.
1. Calculate the surface normals at the vertices of polygons in a 3D computer model.
2. Normals are then averaged for all the polygons that meet at
each vertex.
3. These normals
are interpolated along the edges of the polygons.
4. Lighting computations are then
performed to produce intensities at positions along scanlines.
