Artificial Life: The Coming Evolution

An Overview

Artificial Life

Definition:

The Study Of Man-Made Systems That Exhibit Behaviors Characteristic of Natural Living Systems

Implications:

– Study of life as it could be

– Formal basis for life

– Bottom-up synthesis

– Emergent behavior

– No global controller

Essential Point:

Artificial life studies natural life by attempting to capture the behavioral essence of a living organism

Essential Tool: Computer

(Models on-going behavior not final result)

Essential Features: Computer Based Alife Models

Consist of population of simple programs or specifications

– No single program that directs all other programs

– Each program controls simple entity in environment

– No global rules

– Any behavior at levels higher than program is emergent

Essential Insight: Nature is fundamentally parallel

Historical Roots of Alife

History of Machines

Rendering in hardware actions previously carried out solely by muscle and brain

Early Models: Reflect technology of era

Earliest: Statues/Paintings -- Captured static forms

1st C: Hero of Alexandria -- Treatise on pneumatics (Brief Bio)

· Invented automated theatres that used analogue programming to control the puppets, doors, lights, and sound effects.

· Performed a play lasting 10 minutes and was operated by a complex system of ropes and drums that might be considered to be a means of deciding which parts of the mechanism performed which actions and when

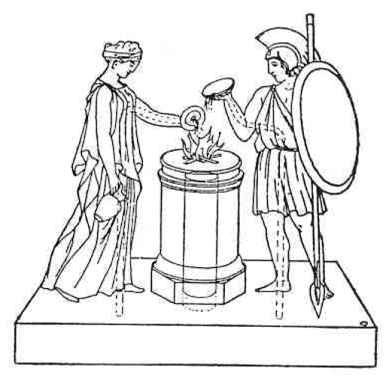
When a fire is lit, the air in the hollow altar expands and drives out the liquid contained in the altar’s pedestal. Then, the liquid passes through tubes in the figure bodies and appears to be poured by the figures.

14th C: Clockwork regulation schemes

17th-18th C: Clockwork mechanisms for mechanical figures

Peak: Mechanical duck of Vaucanson -- gilded copper duck that ate, splashed about and digested food

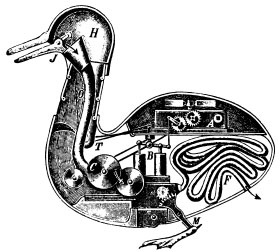
Results: Programmed control

Abstraction of Logical Form of Machine

Formal Application of Logic to Mechanical Process of Arithmetic

Church, Kleene, Godel, Turing, Post -- Logical Sequence of Steps

Realization: An objects dynamical behavior is governed by an abstract control structure -- a program

Implication: Logical form separate from material of construction (e.g. electronic vs mechanical watch)

And: Aliveness is property of logical form

Today: Algorithm is formal equivalent of machine

Formal Limits of Machine Behavior

Computability in Principle

Certain behaviors are uncomputable (i.e. behaviors for which no formal specification exists)

e.g.  Turing's Halting Problem

• Formally specify a machine

• Feed machine a description of another machine,and its initial state

• Ask first machine, by inspection, to determine whether or not second machine will stop

Computability in Practice

A formal specification may exist in principle, but we do not know how to specify in practice

In General

Can not derive behavior from specification nor specification from behavior

Generation of Lifelike Behavior

John Von Neumann- First Computer Approach

· Thought Experiment:  Kinematic Model

§ Machine on surface of pond with machine parts

§ Given description of any machine, it will construct it

§ Given design of self, will copy self

Question: Is this self-replication?

Answer: No!

Fix: Machine must copy description of self into offspring

Note: Constitutes true self-reproduction

Problem: Does not separate logic from material of process

Solution: Cellular Automata (CA)

Cellular Automata Model -- Regular lattice of finite automata

Characteristics:

– Automata can be in only one of a finite number of states

– Transitions from one state to another is governed by state transition tables

– Input derived from states of automata and neighboring sites

– All automata in lattice obey same rules

e.g. Conway's Game of Life

Rules:

– If a cell is dead and has three neighbors at time t, it will become alive at time t+1

– If an alive cell has only one neighbor or more than three neighbors at time t, then at t+1 it will die

Example: http://psoup.math.wisc.edu/mcell/mjcell/mjcell.html

Results of CA Work

– Embedded logical equivalent of his kinematic model within CA using 29 states/cell

– Constructed proof that self-reproduction was achievable by machines

– Showed that information contained in design of machineis used in two different ways

• Interpreted -- As instructions to be executed in the construction of offspring

• Uninterpreted -- As passive data to be duplicated to form a description given to the offspring

Langton Self-Reproducing Cellular Automata (e.g. http://necsi.org/postdocs/sayama/sdsr/java/)

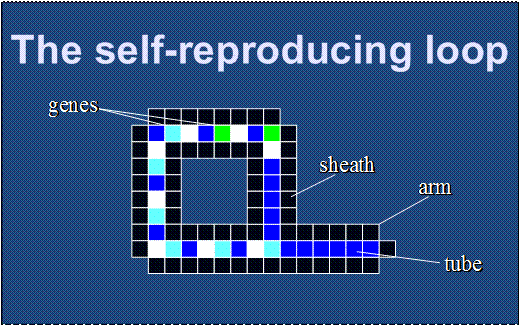
n     Sheath: Outer shell housing gene sequence.

n     Genes: 7s (straight growth) and 4s (turning).

n     Tube: core (1) states within sheath.

n     Arm: extensible loop structure for replication.

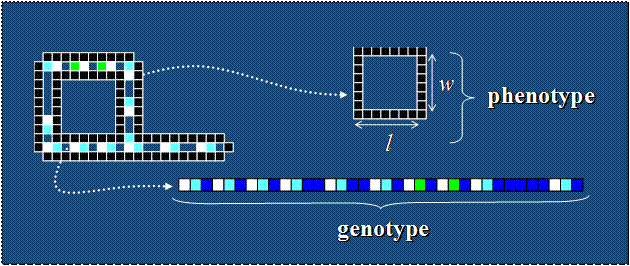
n     Loops composed of phenotype and genotype:

-Phenotype: inner and outer sheath of loop

-Genotype: gene sequence within loop

n     Define loop species by phenotype + genotype.

n     Sufficient information for loop reconstruction.

For details : See http://necsi.org/postdocs/sayama/sdsr/

And http://artis.phenome.org/

Other Work

Weiner -- Feedback control

Walter -- Electronic Turtles

– Small simple three-wheeled autonomous mobile robot whose "brain" consisted of a valve, a relay, and a capacitor

– Capable of apparently complex lifelike behavior, including feeding (charging) when "hungry", pursuing lights, and flocking behaviour in groups.

– Walter called his robot a turtle because it had a turtle-like "shell" on top to protect its electronics.

Stahl  -- Models of Cellular Activity/Metabolism/Reproduction

Lindenmayer -- Models of Cellular Activity and Development

Biological Automata

Question:

Is it possible to abstract logical form of an organism from it's biological wetware?

Definitions:

Genotype -- Specification of machinery  (complete set of low level rules)

Phenotype -- Behavior of machinery  (structure/behavior that emerges in space and time as a  result of the interpretation of the genotype in context of particular environment

Morphogenesis -- Process by which phenotype develops through time under direction of phenotype

Genes -- individual genetic instructions

Problem: Unpredictability of Phenotype From Genotype

General Case:

Cannot determine by inspection alone any non-trivial feature of phenotype that will emerge from a given genotype in context of particular initial configuration

Why? - Non-linear interactions

Solution: Trail-and-error or Natural Selection

General Approach To Building Genotype/Phenotype Systems

(Recursive Generated Objects)

Appeal:

– Arises naturally from Gtype/Ptype distinction

– local development rules - recursively defined - Gtype

– developing structure - recursively generated - Ptype

Under This Method:

– Object is structure that has subparts

– System rules specify how to modify parts and are usually sensitive to context

Lindenmayer Systems (Wikipedia)

(Example)

·Set of rules for recursively rewriting symbols

·E.G. Simple Linear Growth

·Rules for Gtype:

1.  A ->  CB
2.  B ->  A
3.  C ->  DA
4.  D ->  C

Time          Structure
0                A  (Seed)
 1               CB
 2               DAA
 3               CCBCB
 4               etc.

See http://algorithmicbotany.org/papers/

 A forest scene by Reeves,1984 Pixar

A mint Apple twig

From The Algorithmic Beauty of Plants, P. Prusinkiewicz (Book download)

(Properties)

• Can construct branching patterns
• Can be context free or context sensitive
• Context sensitive rules provide for possibility of nonlinear  interactions among parts (feedback control)

Genuine Life In Artificial Life Systems

• Constituent Parts of Alife System Are Different Kinds Of Things From Their Natural Counterparts

But

· Emergence Behavior They Support is Same Kind of Thing

E.G. Boids (Craig Reynold’s examples)

Local Rules:

– Maintain minimum distance from other objects in environment
– Match velocity of Boids in neighborhood
– Move toward perceived center of mass of boids in neighborhood

Result: True Flocking Behavior

Artificial in Alife Refers to Component Parts Not Emergent Processes

Big Claim:

· Properly Organized Sets of Artificial Primitives Carrying Out Same Functional Roles As The Biomolecules in Natural Systems

· Will Support A Process That is "Alive" in The Same Way That Natural Organisms Are Alive

Therefore: Artificial Life Is Genuine Life -- Only Different!

What Are Properties of Life?

1. Pattern in space-time

2. Self-reproduction

3. Information Storage of a Self-representation

4. Metabolism Which Converts Matter And Energy From Environment To Pattern of Activity of The Organism

5. Functions Interactively With Environment

6. Interdependence of Parts

7. Stability Under Perturbations

8. Ability To Evolve

Are Computer Viruses Life Forms?

Biological	Computer
Length of Genetic Material  Injects Code Into Cell Cell Becomes Factory Replicating the Virus	Length of Machine Code Copies Code Into Program When Code Is Executed, Infected Program Spreads Virus Further

Are Viruses Real Life Forms?

1. Viruses are Pattern in Space-time

2. Viruses Self-reproduce

3. Information Storage of a Self-representation is Used For Virus Self-replication

4. Virus Metabolism -- Uses Electricity of Computer

5. Functions Interactively With Environment By Examining Computer Resources

6. Interdependence of Parts -- Can't Divide Virus Into Pieces

7. Stability Under Perturbations -- Virus Can Defeat Anti-Virus and Copy Protection Schemes; Virus Can Adjust to insufficient Memory

8. Ability To Evolve

9. Growth -- Viruses Exhibit Growth By Filling Up Disk Space

Other :

• Can Exist In Well Defined Ecological Niches
• Some Exhibit Predatory Behavior
• Some Exhibit Territorial Behavior

Evolution And Self-Organization

Biological Evolution Is Just One Example of The Tendency of Matter To Organize Itself As Long As Proper Conditions Prevail

Middle 1800's -- H. Spenser

• Evolution Is A Change From Incoherent Homogeneity to Coherent Heterogeneity
• Evolution Gives Rise To:
• Increasing Differentiation (Specialization of Functions)
• Integration (Mutual Interdependence and Coordination of Functions of The Structurally Differentiated Parts)

Self-Organization Simulation by Cellular Automata

(Greenberg-Hastings Model)

· A classical model of excitable media was introduced 1978 by Greenberg and Hastings.

· Two-dimensional square grid G=Z².

· Three Indices:

R, range of interaction

T, Threshold needed for excitation

K, Number of available states

· Rules:

o Each cell on lattice Painted One of K colors arranged in color wheel, 0 -> K-1

o Colors advance in only one direction around color wheel

o Color either advance automatically or by contact

o Advance by color k at site x means that k -> k + 1 IFF at least T neighboring sites within range R of x have values K+1 mod k

o For GH model, only state 0 advances by contact, all other advance automatically

· Neighbors are the five nearest cells, including the cell itself.

Random Seed Converged Dynamics

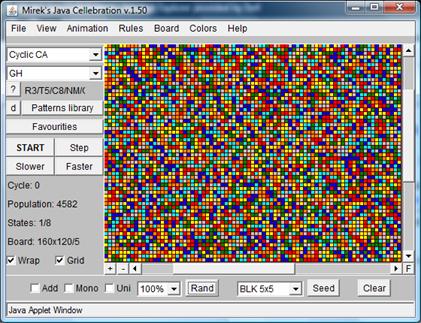
Example: http://psoup.math.wisc.edu/mcell/mjcell/mjcell.html

Reaction-diffusion systems and Morphogenesis

From: Visualization of solid reaction-diffusion systems, Chambers, P.; Rockwood, A., IEEE Computer Graphics and Applications, Volume 15, Issue 5, Sep 1995 Page(s):7 - 11

To explain biological morphogenesis, Alan Turing proposed a system of chemical substances, morphogens, that react together and diffuse throughout the developing tissue.

· The cells within the tissue act as sites for this diffusion and reaction.

· The initial state of the morphogen concentrations may be random or homogeneous.

· However, after the system has evolved, macroscopic concentration patterns appear in the reacting chemicals.

· Local concentration gradients modify the diffusion rates of the morphogens, which react to increase or decrease the amount within individual cells.

The equations describing the two-morphogen reaction-diffusion model are

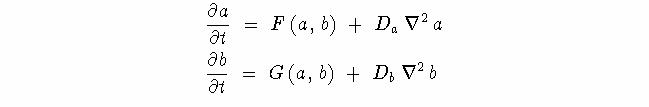
where:

a and b are the concentrations of two diffusing morphogens;

F and G are functions determining the production rate of a and b;

D_a and D_b are diffusion rate constants;

and are the Laplacians of a and b.

• A system to approximate the model is built upon an array of cells through which morphogens a and b may diffuse.
• Within each cell, a and b are created or destroyed according to F and G.

Discretization of Laplace Operator:

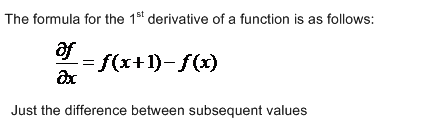
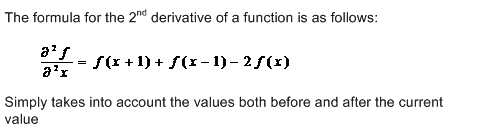
• Turing proposed a discrete system to solve the above equations:

where:

a_i and b_i are morphogen concentrations in a one-dimensional array of cells;

β_i represents the natural variation between individual cells;

s is the reaction rate constant.

1D reaction-diffusion systems

When a 1D reaction-diffusion system evolves, the result is a set of cells whose morphogen concentrations exhibit a large-scale pattern with respect to the dimensions of an individual cell.

The morphogen concentrations, with different colors for different morphogens, are plotted along the y-axis and the cell positions along the x-axis.

• Figure shows the morphogen concentrations for the 1D reaction-diffusion system.
• Morphogen a is plotted in red and morphogen b in green. The zero-morphogen baseline is blue.

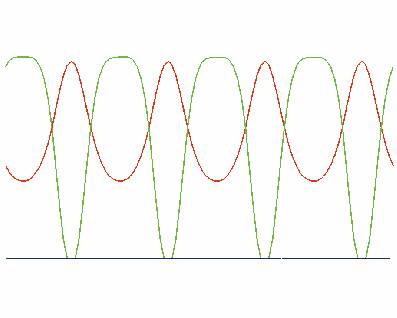
· Simulation uses the following values: D_a = 0.25, D_b = 0.0625, a_i = 4.0, b_i = 4.0, β_i = 12.0 ? 0.05 (randomly selected for each i), s = 0.00625, number of cells = 100, iterations = 60,000.

· This defines a homogeneous starting condition.

· After 60,000 iterations, the system acquires a macroscopic organization with symmetric highs and lows of morphogen concentration.

· The peaks of morphogen a’s concentration match the lows of morphogen b’s concentration, and vice-versa.

· This is characteristic of a two-morphogen system; high concentrations of morphogen a inhibit further similar regions from forming close by.

2D reaction-diffusion systems

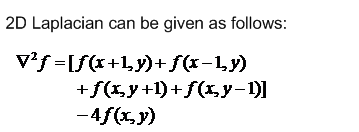
In Matrix form:

The discrete reaction-diffusion equations extend to two dimensions:

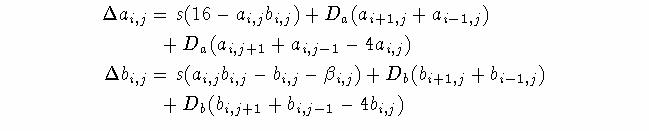
• Cells are arranged on a square grid.
• Each cell diffuses to and from its four neighbors, with periodic boundary conditions.
• Visualizing 2D systems uses morphogen intensity mapping
• 2D grid is shaded according to the amount of a particular morphogen contained in the corresponding cell.
• Dark areas are regions of low morphogen concentration, while lighter areas represent higher concentrations.
• The choice of color is arbitrary.
• Initial conditions of a 2D reaction-diffusion system are the same as the 1D case, except s = 0.03125.
• The system consists of 80 by 80 cells and runs for 20,000 iterations.

• Intensity map visualization of the reaction-diffusion data.
• The areas of minimum concentration form clearly defined regions with smooth transitions to adjacent cells.
• Patterns such as this underlie much of the work on mammalian coat patterns.

Imposition of external control upon the diffusion parameters Da and Db.

The anisotropy biases the system to form stable domains parallel to the direction of the greatest b morphogen diffusion rate. Note the resemblance to zebra stripes.

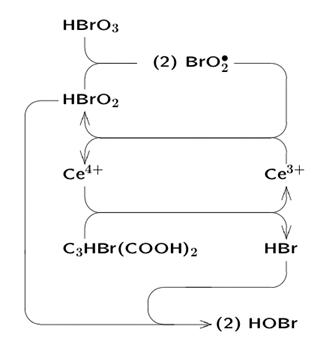
Belousov-Zhabotinsky reaction – Oscillatory Reactions

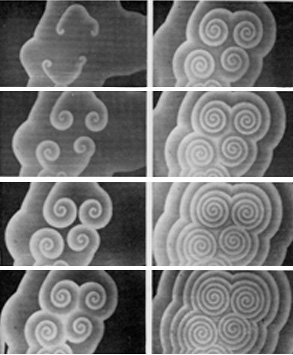
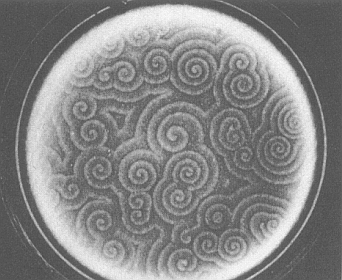
Slime Mold

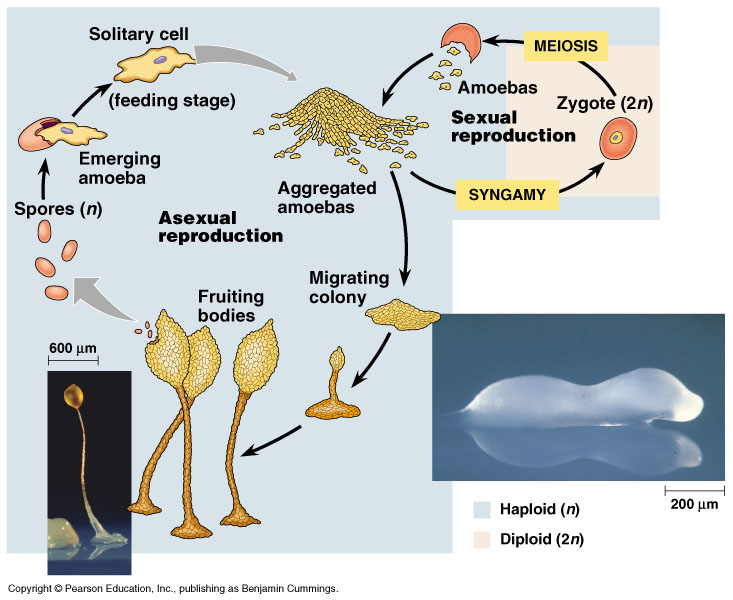
What’s Next?