|
Computing
with DNA |
Invented
(discovered?) by Dr. Leonard M. Adleman of USC in
1994, a computer scientist and mathematician
Basic
Idea: Perform
molecular biology experiment to find solution to math problem.
“DNA Computer”
“Biological Computation” vs “computational biology”
“Molecular Computer”
Why DNA Computing?
o
Radically different computational paradigm
o
Observe that DNA is just another ‘code’ that can be manipulated.
o
Computation is typically viewed as ‘string processing’ of some
form.
o
Computation is implemented by biological molecules and manipulation
mechanisms – e.g. usual DNA reproductive mechanisms, enzymes catalyse particular joining, shortening, extension
manipulations etc.
o
Fundamental is the notion of Crick Watson complementarity
Still: Why DNA Computing?
o
Support
for standard computation
o
Better
understanding of how nature computes
o
New
data structures (molecules)
o
New
operations - l cut, paste, adjoin, insert, delete, ...
o
New
computability models.
Key Features of DNA Computing
·
Massive
parallelism of DNA strands high density of information storage ease of
constructing many copies
·
Watson-Crick
complementarity – yields universality, in the Turing sense
o
feature
provided „for free“
o
universal
twin shuffle language
Twin-shuffle language
TS consists of all words over the alphabet
{0,1,0’,1’} obtained thus –
o
Take
an arbitrary word w over {0,1} and its complement w’
and shuffle the letters, keeping the order of letters from each word the same.
o
Twin-shuffle
languages are universal: for every recursively enumerable language L, there is
a mapping g such that L=g(TS)
o
e.g. Consider set of all possible words (sequences) that can be obtained
from two given words by shuffling them without changing the order of letters.
§
For
instance, shuffling AG and TC we get AGTC, ATCG, TCAG and TAGC.
§
Then
collect all shufflings of all pairs of complementary
words into the so-called twin-shuffle language.
§
There
is a simple way to go from a DNA double strand to a word in the twin-shuffle language
and back.
§
Universality
follows from the fact that any Turing computation can be performed by using an
appropriate finite automaton to filter the (fixed) twin-shuffle language.
§
So
DNA computers could in theory perform any operation that digital computers can.
|
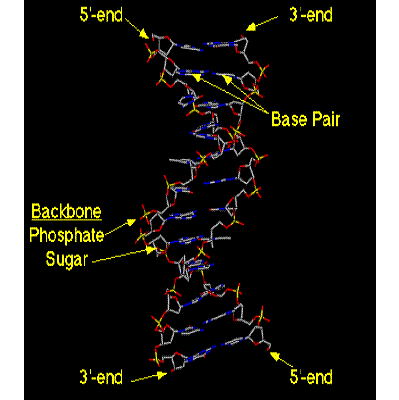
The double helix Two DNA strands, each a
right-handed helix Strands are anti-parallel - the
chains run from 3’ to 5’ in opposite directions The primary sugarphosphate
structure of the two DNA strands wind around the helix axis with the bases of
the individual nucleotides on the inside of the helix. |
|
(image from http://www.blc.arizona.edu/Molecular_Graphics/DNA_Structure/DNA_Tutorial.HTML
)
Base Pairing in DNA
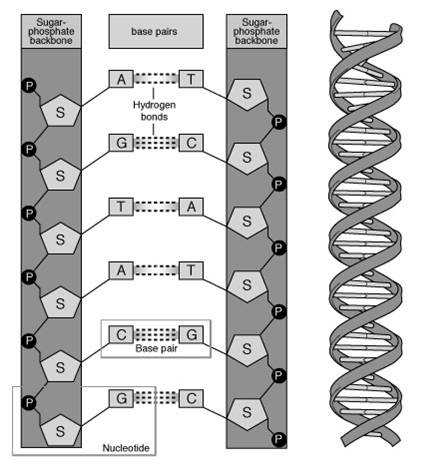
( from http://www.accessexcellence.org/RC/VL/GG/dna2.php
)
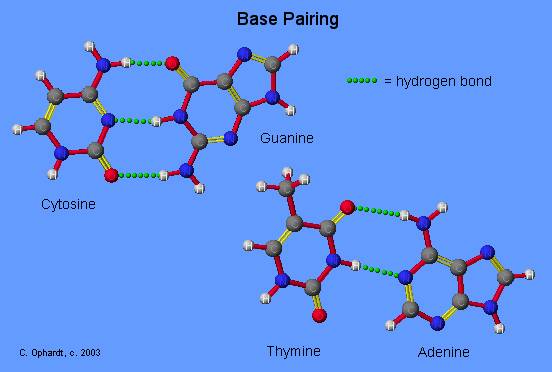
Watson-Crick Complementarity:
AT and CG
DNA Synthesis
·
Getting
bits of DNA with specified sequences is really not a problem
·
Oligonucleotides (short strands of DNA) can be made in the lab with a
synthesizer
– Supply
bottled of A, C, G and T in solution to the synthesizer
–
Specify the sequence
– Turn
it on!
·
Millions
of copies of the required sequence are produced and placed in solution
·
…or
just buy them by mail order!
Denaturing, annealing and ligation
Denaturing =
melting = separation of dsDNS (double stranded) into
two complementary ssDNA (single stranded)
–
Achieved
by heating the solution to ~90-95deg
Annealing
is the reverse of denaturing
–
Solution
of ssDNA is cooled, allows strands to join together again
Ligation is the joining of two nucleotides together
–
For
example, join two strands ssDNA end to end
–
Ligase is the enzyme that does this
–
Can
also repair breaks in one strand of dsDNA
Cutting DNA - Restriction
Enzymes (molecular machines) are
used to cut DNA sugar-phosphate backbone
–
Enzymes look for a specific sequence of bases
– Cuts
may be asymmetric – “sticky ends”
– Cuts may be within or outside the
enzyme’s recognition site
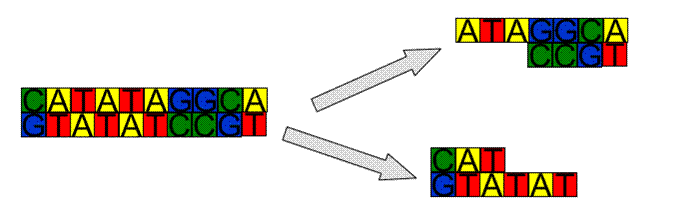
Joining DNA – Ligation
·
Reverse
of cutting is also accomplished by enzymes
·
Where
we have “sticky” ends (one strand longer than the other) we must have the exact
complement for it to work.
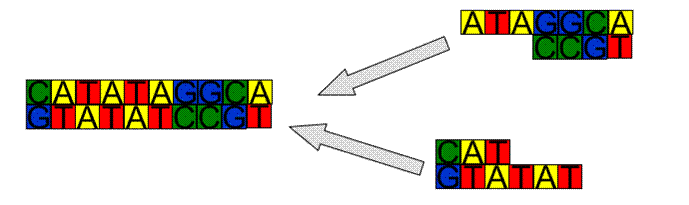
Copying DNA - Polymerisation
·
At
some stage we are going to need to make copies of DNA sequences
·
Assume
the molecule has ends γ and β, denote the WC complement of a sequence
of bases by h(.)

·
Heat
the dsDNA up to split it into two ssDNA

· Primers h(γ) and h(β) in
the mixture that bind to the ends of the ssDNA

·
Once
this is done, a DNA polymerase fills in the rest of the missing bases to
complete the dsDNA.
·
The
same is done for the complementary strand, so we end up with two strands the
same.
Amplifying DNA - PCR
The
polymerase chain reaction can be used to amplify DNA.
– Template (strand to copy) is denatured at
high temp. (~ 95oC)
– It is cooled to a temperature that
will allow optimal primer binding.
– The reaction temperature is then
raised to that optimal for the DNA polymerase (~ 72oC) so the primers are
extended along the template.
– This series of steps is carried out 20
- 30 times leading to exponential amplification of the target template.
Separating DNA – Hybridization
·
Allows
us to separate out molecules with a known DNA sequence from a mix of different
sequences
·
To
detect a particular sequence of bases, we generate many copies of a probe – single strand of DNA bases that is WC
complement of the target
·
Attach
these probes to biotin molecule
·
Bind
biotin to a fixed matrix or magnetic beads
·
Pour
the mix of sequences over the probes
·
When
target meets the probe they bind
·
Non-binding
strands can be washed away
·
Targets
then removed from matrix back into solution
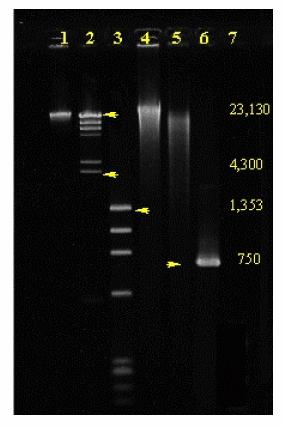
Separating DNA - Electrophoresis
|
• Separation is based on size = length of
strands • DNA mixture loaded onto one edge of gel • An electric field is applied across the gel • How far a strand moves depends on its mass – Logarithmic separation with length |
|
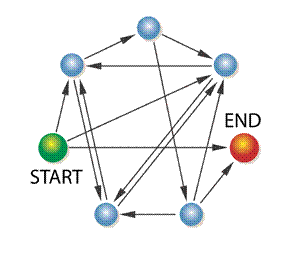
First DNA Computing Problem
HAMILTONIAN
PATH PROBLEM (Posed
by William Hamilton)
Given a
network of nodes and directed connections between them, is there a path through
the network that begins with the start node and concludes with the end node
visiting each node only once (“Hamiltonian path")?
Adleman, L.M. “Molecular Computation of
Solutions to Combinatorial Problems.” Science. 266: 1021-1024
(Nov. 11, 1994). (PDF)
Adelman’s
Scientific American paper (PDF)
·
Hamiltonian
path problem with 7 cities and 14 connections.
·
With
DNA, the initial state is created by synthesizing DNA molecules with a certain
sequence and after some reactions, a new molecule is
produced with the answer.
·
It
took one second for the DNA to come up with answers, but it took him a week to
dig out the answer from the DNA soup
“Does a Hamiltonian
path exist, or not?”
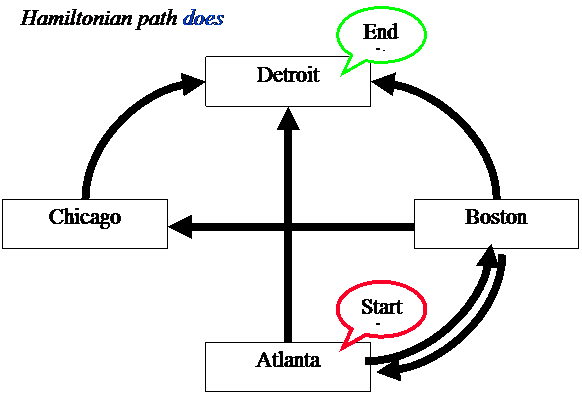

Problems that are NP Complete (Nondeterministic Polynomial time)
·
Hard NP problem - the time required for algorithms
to find a solution increases exponentially with the number of variables
involved.
·
Easy NP problem - the algorithm running time
increases in proportion to the number of variables.)
·
A
hard NP problem can eat up a lot of computer cycles if carried out by brute
force.
o
e.g. the
§
for N cities, there are N!/2 possible paths.
§
As
the number of cities grows, the number of possible path combinations soars.
§
9
cities - 180,000 possible paths.
§
11
cities - 19.8 million paths,
§
13
cities - 3 billion paths,
§
17
cities - 200 trillion paths.
Solving the Hamiltonian Problem
Typical Algorithm - Generation-&-Test:
Step 1: Generate random paths on the network.
Step 2: Keep only those paths that begin with
start city and conclude with end city.
Step 3: If there are N cities, keep only those
paths of length N.
Step 4: Keep only those that enter all cities
at least once.
Step 5. Any remaining
paths are solutions (i.e., Hamiltonian paths).
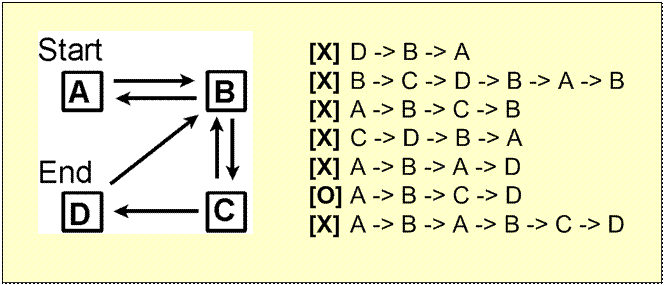
Does
a Hamiltonian path exist for the following network?
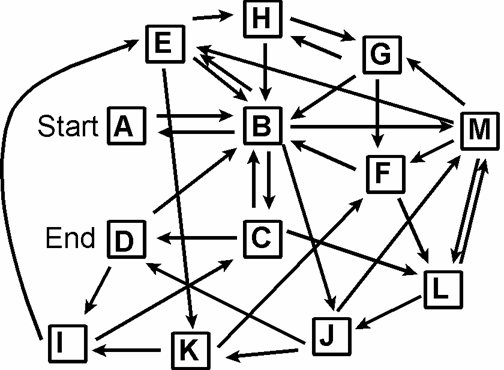
Combinatorial Explosion
The total
number of paths grows exponentially as the network size increases:
(e.g.) 106
paths for N=10 cities, 1012 paths (N=20), 10100 paths!! (N =100)
·
The
Generation-&-Test algorithm takes “forever”.
·
Some
sort of smart algorithm must be devised; none has been found so far (NP-hard).
DNA for Hamiltonian Problem
The key to
solving the problem is using DNA to perform the five steps of the
Generation-&-Test algorithm in parallel search, instead of serial
search.
Adelman’s algorithm
1. Produce strands corresponding to vertices and
edges
2. Generate many paths in the graph, randomly
3. Remove all paths that do not start at vertex vi
or end on
vertex vo
4. Remove all paths that do not involve exactly n
vertices
5. For each of the n vertices v, remove all
paths that do not involve v.
• Steps 2,3, 4 are
constant time, 1,5 are polynomial in n
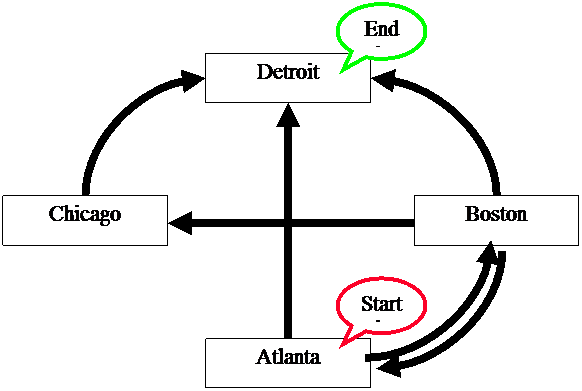
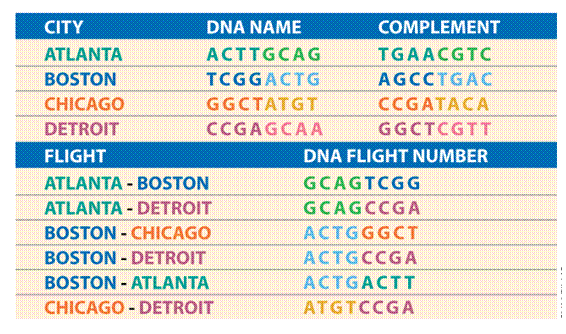
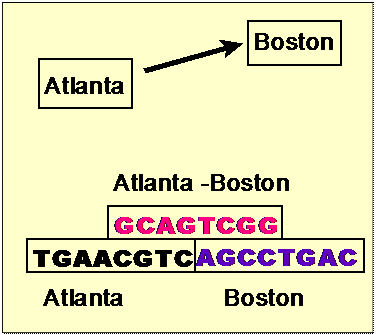
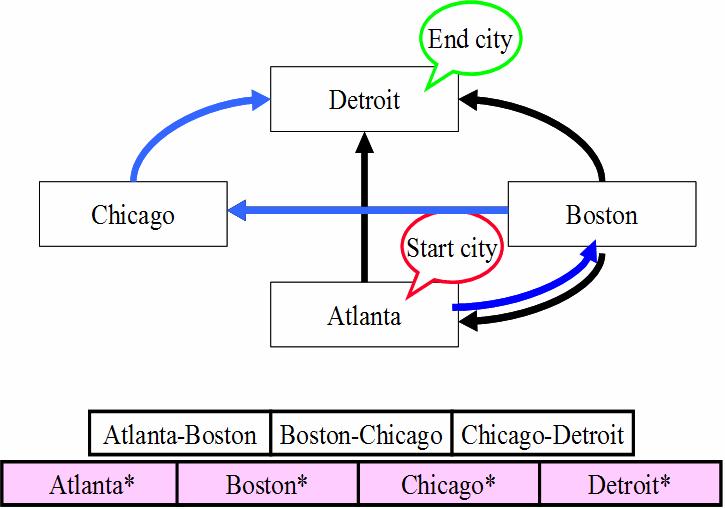
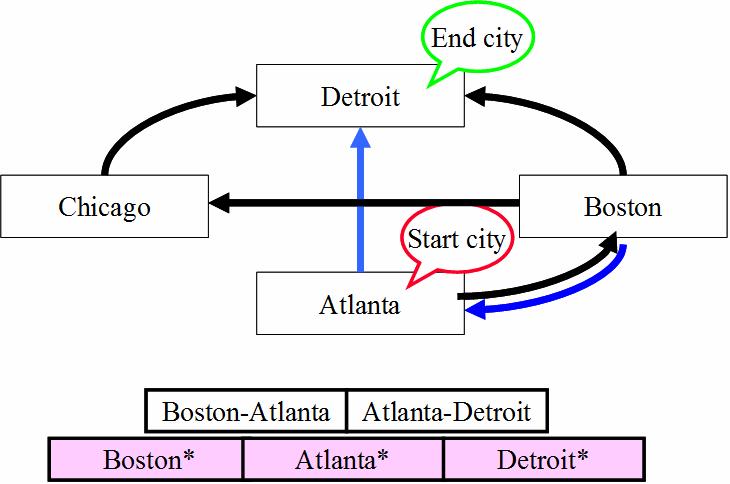
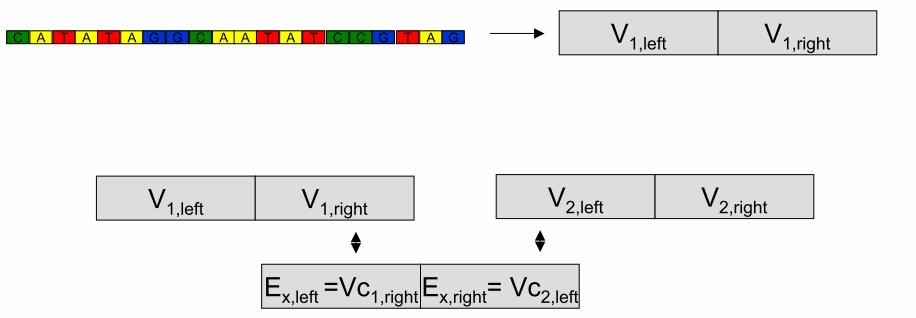
DNA encoding of city-network
Vertex and Edge Encodings
Each city vi
is encoded by two sub-sequences:
vi = vi´ vi´´ the base complements.
Each flight eik
from vi to vk is encoded by:
eik =vi´´vk´
Aldleman’s Data Representation
7 Cities
• Each node represented by a 20-mer
strand
• Each possible edge represented by a
complementary 20-mer
DNA Experiment
|
1. In a
test tube, mix the prepared DNA pieces together (which will randomly link with each other, forming all different
paths). 2.
Perform PCR with two ‘start’ and ‘end’ DNA pieces as primers (which creates
millions’ copies of DNA strands with the right start and end). 3.
Perform gel electrophoresis to identify only those pieces of right length
(e.g., N=4). 4. Use
DNA ‘probe’ molecules to check whether their paths pass through all
intermediate cities. 5. All
DNA pieces that are left in the tube should be precisely those representing
Hamiltonian paths. - If the
tube contains any DNA at all, then conclude that a Hamiltonian path exists,
and otherwise not. - When
it does, the DNA sequence represents the specific path of the solution. |
DNA Experiment Set-up
Ingredients
and tools needed:
- DNA strands that encode city names and
connections between them
- Polymerases, ligase,
water, salt, other ingredients
- Polymerase chain reaction (PCR) set
- Gel electrophoresis tool (that filters
out non-solution strands)
Gel Electrophoresis

o
DNA
molecules are negatively charged.
o
Placed
in an electric field, they will move towards the positive electrode.
o
The
negative charge is proportional to the length of the DNA molecule.
o
The
force needed to move the molecule is proportional to its length.
o
A
gel makes the molecules move at different speeds.
o
DNA
molecules are invisible, and must be marked (ethidium
bromide, radioactive)
SUMMARY
& CONCLUSION
o
Why
does it work?
Enormous parallelism, with 1023 DNA
pieces working in parallel to find solution simultaneously.
Takes less than a week (vs.
thousands yrs for supercomputer)
o
Massively
parallel information processing:
o
106
ops / sec for PCs
o
1012
ops / sec for supercomputers
o
1020
ops / sec possible for DNA
o DNA computers would be >
1,000,000 times faster than any computer today.
o
Extraordinary
energy efficient (10-10 of
supercomputer energy use)