CS865 – Distributed Software Development

Tannenbaum and Van Steen – Chapter 8

Fault Tolerance

A characteristic feature of distributed systems that distinguishes them from single-machine systems is the notion of partial failure. A partial failure may happen when one component in a distributed system fails. This failure may affect the proper operation of other components, while at the same time leaving yet other components totally unaffected. In contrast, a failure in nondistributed systems is often total in the sense that it affects all components, and may easily bring down the entire system.

An important goal in distributed systems design is to construct the system in such a way that it can automatically recover from partial failures without seriously affecting the overall performance. In particular, whenever a failure occurs, the distributed system should continue to operate in an acceptable way while repairs are being made, that is, it should tolerate faults and continue to operate to some extent even in their presence.

In this chapter, we take a closer look at techniques for making distributed systems fault tolerant. After providing some general background on fault tolerance, we will look at process resilience and reliable multicasting. Process resilience incorporates techniques by which one or more processes can fail without seriously disturbing the rest of the system. Related to this issue is reliable multicasting, by which message transmission to a collection of processes is guaranteed to succeed. Reliable multicasting is often necessary to keep processes synchronized.

Atomicity is a property that is important in many applications. For example, in distributed transactions, it is necessary to guarantee that every operation in a transaction is carried out or none of them are. Fundamental to atomicity in distributed systems is the notion of distributed commit protocols, which are discussed in a separate section in this chapter.

[Page 322]

Finally, we will examine how to recover from a failure. In particular, we consider when and how the state of a distributed system should be saved to allow recovery to that state later on.

8.1. Introduction to Fault Tolerance

Fault tolerance has been subject to much research in computer science. In this section, we start with presenting the basic concepts related to processing failures, followed by a discussion of failure models. The key technique for handling failures is redundancy, which is also discussed. For more general information on fault tolerance in distributed systems, see, for example Jalote (1994) or (Shooman, 2002).

8.1.1. Basic Concepts

To understand the role of fault tolerance in distributed systems we first need to take a closer look at what it actually means for a distributed system to tolerate faults. Being fault tolerant is strongly related to what are called dependable systems. Dependability is a term that covers a number of useful requirements for distributed systems including the following (Kopetz and Verissimo, 1993):

1. Availability

2. Reliability

3. Safety

4. Maintainability

Availability is defined as the property that a system is ready to be used immediately. In general, it refers to the probability that the system is operating correctly at any given moment and is available to perform its functions on behalf of its users. In other words, a highly available system is one that will most likely be working at a given instant in time.

Reliability refers to the property that a system can run continuously without failure. In contrast to availability, reliability is defined in terms of a time interval instead of an instant in time. A highly-reliable system is one that will most likely continue to work without interruption during a relatively long period of time. This is a subtle but important difference when compared to availability. If a system goes down for one millisecond every hour, it has an availability of over 99.9999 percent, but is still highly unreliable. Similarly, a system that never crashes but is shut down for two weeks every August has high reliability but only 96 percent availability. The two are not the same.

[Page 323]

Safety refers to the situation that when a system temporarily fails to operate correctly, nothing catastrophic happens. For example, many process control systems, such as those used for controlling nuclear power plants or sending people into space, are required to provide a high degree of safety. If such control systems temporarily fail for only a very brief moment, the effects could be disastrous. Many examples from the past (and probably many more yet to come) show how hard it is to build safe systems.

Finally, maintainability refers to how easy a failed system can be repaired. A highly maintainable system may also show a high degree of availability, especially if failures can be detected and repaired automatically. However, as we shall see later in this chapter, automatically recovering from failures is easier said than done.

Often, dependable systems are also required to provide a high degree of security, especially when it comes to issues such as integrity. We will discuss security in the next chapter.

A system is said to fail when it cannot meet its promises. In particular, if a distributed system is designed to provide its users with a number of services, the system has failed when one or more of those services cannot be (completely) provided. An error is a part of a system's state that may lead to a failure. For example, when transmitting packets across a network, it is to be expected that some packets have been damaged when they arrive at the receiver. Damaged in this context means that the receiver may incorrectly sense a bit value (e.g., reading a 1 instead of a 0), or may even be unable to detect that something has arrived.

The cause of an error is called a fault. Clearly, finding out what caused an error is important. For example, a wrong or bad transmission medium may easily cause packets to be damaged. In this case, it is relatively easy to remove the fault. However, transmission errors may also be caused by bad weather conditions such as in wireless networks. Changing the weather to reduce or prevent errors is a bit trickier.

Building dependable systems closely relates to controlling faults. A distinction can be made between preventing, removing, and forecasting faults (Avizienis et al., 2004). For our purposes, the most important issue is fault tolerance, meaning that a system can provide its services even in the presence of faults. In other words, the system can tolerate faults and continue to operate normally.

Faults are generally classified as transient, intermittent, or permanent. Transient faults occur once and then disappear. If the operation is repeated, the fault goes away. A bird flying through the beam of a microwave transmitter may cause lost bits on some network (not to mention a roasted bird). If the transmission times out and is retried, it will probably work the second time.

An intermittent fault occurs, then vanishes of its own accord, then reappears, and so on. A loose contact on a connector will often cause an intermittent fault. Intermittent faults cause a great deal of aggravation because they are difficult to diagnose. Typically, when the fault doctor shows up, the system works fine.

[Page 324]

A permanent fault is one that continues to exist until the faulty component is replaced. Burnt-out chips, software bugs, and disk head crashes are examples of permanent faults.

8.1.2. Failure Models

A system that fails is not adequately providing the services it was designed for. If we consider a distributed system as a collection of servers that communicate with one another and with their clients, not adequately providing services means that servers, communication channels, or possibly both, are not doing what they are supposed to do. However, a malfunctioning server itself may not always be the fault we are looking for. If such a server depends on other servers to adequately provide its services, the cause of an error may need to be searched for somewhere else.

Such dependency relations appear in abundance in distributed systems. A failing disk may make life difficult for a file server that is designed to provide a highly available file system. If such a file server is part of a distributed database, the proper working of the entire database may be at stake, as only part of its data may be accessible.

To get a better grasp on how serious a failure actually is, several classification schemes have been developed. One such scheme is shown in Fig. 8-1, and is based on schemes described in Cristian (1991) and Hadzilacos and Toueg (1993).

Figure 8-1. Different types of failures.

A crash failure occurs when a server prematurely halts, but was working correctly until it stopped. An important aspect of crash failures is that once the server has halted, nothing is heard from it anymore. A typical example of a crash failure is an operating system that comes to a grinding halt, and for which there is only one solution: reboot it. Many personal computer systems suffer from crash failures so often that people have come to expect them to be normal. Consequently, moving the reset button from the back of a cabinet to the front was done for good reason. Perhaps one day it can be moved to the back again, or even removed altogether.

[Page 325]

An omission failure occurs when a server fails to respond to a request. Several things might go wrong. In the case of a receive omission failure, possibly the server never got the request in the first place. Note that it may well be the case that the connection between a client and a server has been correctly established, but that there was no thread listening to incoming requests. Also, a receive omission failure will generally not affect the current state of the server, as the server is unaware of any message sent to it.

Likewise, a send omission failure happens when the server has done its work, but somehow fails in sending a response. Such a failure may happen, for example, when a send buffer overflows while the server was not prepared for such a situation. Note that, in contrast to a receive omission failure, the server may now be in a state reflecting that it has just completed a service for the client. As a consequence, if the sending of its response fails, the server has to be prepared for the client to reissue its previous request.

Other types of omission failures not related to communication may be caused by software errors such as infinite loops or improper memory management by which the server is said to "hang."

Another class of failures is related to timing. Timing failures occur when the response lies outside a specified real-time interval. As we saw with isochronous data streams in Chap. 4, providing data too soon may easily cause trouble for a recipient if there is not enough buffer space to hold all the incoming data. More common, however, is that a server responds too late, in which case a performance failure is said to occur.

A serious type of failure is a response failure, by which the server's response is simply incorrect. Two kinds of response failures may happen. In the case of a value failure, a server simply provides the wrong reply to a request. For example, a search engine that systematically returns Web pages not related to any of the search terms used, has failed.

The other type of response failure is known as a state transition failure. This kind of failure happens when the server reacts unexpectedly to an incoming request. For example, if a server receives a message it cannot recognize, a state transition failure happens if no measures have been taken to handle such messages. In particular, a faulty server may incorrectly take default actions it should never have initiated.

The most serious are arbitrary failures, also known as Byzantine failures. In effect, when arbitrary failures occur, clients should be prepared for the worst. In particular, it may happen that a server is producing output it should never have produced, but which cannot be detected as being incorrect Worse yet a faulty server may even be maliciously working together with other servers to produce intentionally wrong answers. This situation illustrates why security is also considered an important requirement when talking about dependable systems. The term "Byzantine" refers to the Byzantine Empire, a time (330–1453) and place (the Balkans and modern Turkey) in which endless conspiracies, intrigue, and untruthfulness were alleged to be common in ruling circles. Byzantine faults were first analyzed by Pease et al. (1980) and Lamport et al. (1982). We return to such failures below.

[Page 326]

Arbitrary failures are closely related to crash failures. The definition of crash failures as presented above is the most benign way for a server to halt. They are also referred to as fail-stop failures. In effect, a fail-stop server will simply stop producing output in such a way that its halting can be detected by other processes. In the best case, the server may have been so friendly to announce it is about to crash; otherwise it simply stops.

Of course, in real life, servers halt by exhibiting omission or crash failures, and are not so friendly as to announce in advance that they are going to stop. It is up to the other processes to decide that a server has prematurely halted. However, in such fail-silent systems, the other process may incorrectly conclude that a server has halted. Instead, the server may just be unexpectedly slow, that is, it is exhibiting performance failures.

Finally, there are also occasions in which the server is producing random output, but this output can be recognized by other processes as plain junk. The server is then exhibiting arbitrary failures, but in a benign way. These faults are also referred to as being fail-safe.

8.1.3. Failure Masking by Redundancy

If a system is to be fault tolerant, the best it can do is to try to hide the occurrence of failures from other processes. The key technique for masking faults is to use redundancy. Three kinds are possible: information redundancy, time redundancy, and physical redundancy [see also Johnson (1995)]. With information redundancy, extra bits are added to allow recovery from garbled bits. For example, a Hamming code can be added to transmitted data to recover from noise on the transmission line.

With time redundancy, an action is performed, and then, if need be, it is performed again. Transactions (see Chap. 1) use this approach. If a transaction aborts, it can be redone with no harm. Time redundancy is especially helpful when the faults are transient or intermittent.

With physical redundancy, extra equipment or processes are added to make it possible for the system as a whole to tolerate the loss or malfunctioning of some components. Physical redundancy can thus be done either in hardware or in software. For example, extra processes can be added to the system so that if a small number of them crash, the system can still function correctly. In other words, by replicating processes, a high degree of fault tolerance may be achieved. We return to this type of software redundancy below.

[Page 327]

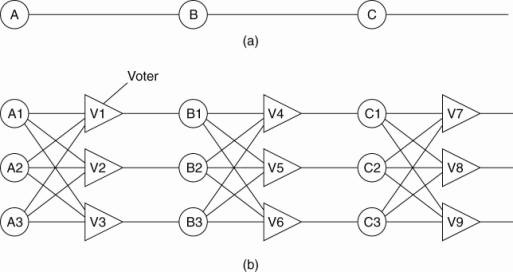
Physical redundancy is a well-known technique for providing fault tolerance. It is used in biology (mammals have two eyes, two ears, two lungs, etc.), aircraft (747s have four engines but can fly on three), and sports (multiple referees in case one misses an event). It has also been used for fault tolerance in electronic circuits for years; it is illustrative to see how it has been applied there. Consider, for example, the circuit of Fig. 8-2(a). Here signals pass through devices A, B, and C, in sequence. If one of them is faulty, the final result will probably be incorrect.

Figure 8-2. Triple modular redundancy.

In Fig. 8-2(b), each device is replicated three times. Following each stage in the circuit is a triplicated voter. Each voter is a circuit that has three inputs and one output. If two or three of the inputs are the same, the output is equal to that input. If all three inputs are different, the output is undefined. This kind of design is known as TMR (Triple Modular Redundancy).

Suppose that element A2 fails. Each of the voters, V1, V2, and V3 gets two good (identical) inputs and one rogue input, and each of them outputs the correct value to the second stage. In essence, the effect of A2 failing is completely masked, so that the inputs to B1, B2, and B3 are exactly the same as they would have been had no fault occurred.

Now consider what happens if B3 and C1 are also faulty, in addition to A2. These effects are also masked, so the three final outputs are still correct.

At first it may not be obvious why three voters are needed at each stage. After all, one voter could also detect and pass though the majority view. However, a voter is also a component and can also be faulty. Suppose, for example, that voter V1 malfunctions. The input to B1 will then be wrong, but as long as everything else works, B2 and B3 will produce the same output and V4, V5, and V6 will all produce the correct result into stage three. A fault in V1 is effectively no different than a fault in B1. In both cases B1 produces incorrect output, but in both cases it is voted down later and the final result is still correct.

[Page 328]

Although not all fault-tolerant distributed systems use TMR, the technique is very general, and should give a clear feeling for what a fault-tolerant system is, as opposed to a system whose individual components are highly reliable but whose organization cannot tolerate faults (i.e., operate correctly even in the presence of faulty components). Of course, TMR can be applied recursively, for example, to make a chip highly reliable by using TMR inside it, unknown to the designers who use the chip, possibly in their own circuit containing multiple copies of the chips along with voters.

8.2. Process Resilience

Now that the basic issues of fault tolerance have been discussed, let us concentrate on how fault tolerance can actually be achieved in distributed systems. The first topic we discuss is protection against process failures, which is achieved by replicating processes into groups. In the following pages, we consider the general design issues of process groups, and discuss what a fault-tolerant group actually is. Also, we look at how to reach agreement within a process group when one or more of its members cannot be trusted to give correct answers.

8.2.1. Design Issues

The key approach to tolerating a faulty process is to organize several identical processes into a group. The key property that all groups have is that when a message is sent to the group itself, all members of the group receive it. In this way, if one process in a group fails, hopefully some other process can take over for it (Guerraoui and Schiper, 1997).

Process groups may be dynamic. New groups can be created and old groups can be destroyed. A process can join a group or leave one during system operation. A process can be a member of several groups at the same time. Consequently, mechanisms are needed for managing groups and group membership.

Groups are roughly analogous to social organizations. Alice might be a member of a book club, a tennis club, and an environmental organization. On a particular day, she might receive mailings (messages) announcing a new birthday cake cookbook from the book club, the annual Mother's Day tennis tournament from the tennis club, and the start of a campaign to save the Southern groundhog from the environmental organization. At any moment, she is free to leave any or all of these groups, and possibly join other groups.

The purpose of introducing groups is to allow processes to deal with collections of processes as a single abstraction. Thus a process can send a message to a group of servers without having to know who they are or how many there are or where they are, which may change from one call to the next.

Flat Groups versus Hierarchical Groups

An important distinction between different groups has to do with their internal structure. In some groups, all the processes are equal. No one is boss and all decisions are made collectively. In other groups, some kind of hierarchy exists. For example, one process is the coordinator and all the others are workers. In this model, when a request for work is generated, either by an external client or by one of the workers, it is sent to the coordinator. The coordinator then decides which worker is best suited to carry it out, and forwards it there. More complex hierarchies are also possible, of course. These communication patterns are illustrated in Fig. 8-3.

Figure 8-3. (a) Communication in a flat group. (b) Communication in a simple hierarchical group.

[

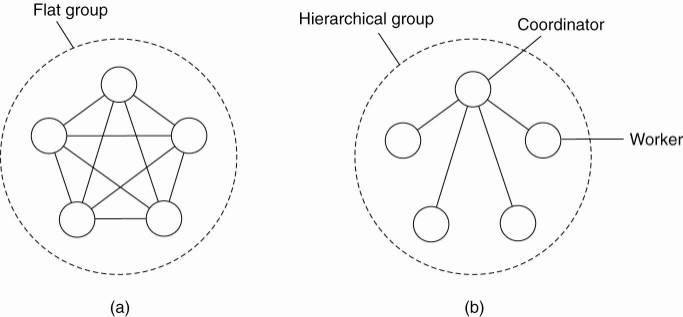
Each of these organizations has its own advantages and disadvantages. The flat group is symmetrical and has no single point of failure. If one of the processes crashes, the group simply becomes smaller, but can otherwise continue. A disadvantage is that decision making is more complicated. For example, to decide anything, a vote often has to be taken, incurring some delay and overhead.

The hierarchical group has the opposite properties. Loss of the coordinator brings the entire group to a grinding halt, but as long as it is running, it can make decisions without bothering everyone else.

Group Membership

When group communication is present, some method is needed for creating and deleting groups, as well as for allowing processes to join and leave groups. One possible approach is to have a group server to which all these requests can be sent. The group server can then maintain a complete data base of all the groups and their exact membership. This method is straightforward, efficient, and fairly easy to implement. Unfortunately, it shares a major disadvantage with all centralized techniques: a single point of failure. If the group server crashes, group management ceases to exist. Probably most or all groups will have to be reconstructed from scratch, possibly terminating whatever work was going on.

[Page 330]

The opposite approach is to manage group membership in a distributed way. For example, if (reliable) multicasting is available, an outsider can send a message to all group members announcing its wish to join the group .

Ideally, to leave a group, a member just sends a goodbye message to everyone. In the context of fault tolerance, assuming fail-stop semantics is generally not appropriate. The trouble is, there is no polite announcement that a process crashes as there is when a process leaves voluntarily. The other members have to discover this experimentally by noticing that the crashed member no longer responds to anything. Once it is certain that the crashed member is really down (and not just slow), it can be removed from the group.

Another knotty issue is that leaving and joining have to be synchronous with data messages being sent. In other words, starting at the instant that a process has joined a group, it must receive all messages sent to that group. Similarly, as soon as a process has left a group, it must not receive any more messages from the group, and the other members must not receive any more messages from it. One way of making sure that a join or leave is integrated into the message stream at the right place is to convert this operation into a sequence of messages sent to the whole group.

One final issue relating to group membership is what to do if so many machines go down that the group can no longer function at all. Some protocol is needed to rebuild the group. Invariably, some process will have to take the initiative to start the ball rolling, but what happens if two or three try at the same time? The protocol must to be able to withstand this.

8.2.2. Failure Masking and Replication

Process groups are part of the solution for building fault-tolerant systems. In particular, having a group of identical processes allows us to mask one or more faulty processes in that group. In other words, we can replicate processes and organize them into a group to replace a single (vulnerable) process with a (fault tolerant) group. As discussed in the previous chapter, there are two ways to approach such replication: by means of primary-based protocols, or through replicated-write protocols.

Primary-based replication in the case of fault tolerance generally appears in the form of a primary-backup protocol. In this case, a group of processes is organized in a hierarchical fashion in which a primary coordinates all write operations. In practice, the primary is fixed, although its role can be taken over by one of the backups, if need be. In effect, when the primary crashes, the backups execute some election algorithm to choose a new primary.

[Page 331]

As we explained in the previous chapter, replicated-write protocols are used in the form of active replication, as well as by means of quorum-based protocols. These solutions correspond to organizing a collection of identical processes into a flat group. The main advantage is that such groups have no single point of failure, at the cost of distributed coordination.

An important issue with using process groups to tolerate faults is how much replication is needed. To simplify our discussion, let us consider only replicated-write systems. A system is said to be k fault tolerant if it can survive faults in k components and still meet its specifications. If the components, say processes, fail silently, then having k + 1 of them is enough to provide k fault tolerance. If k of them simply stop, then the answer from the other one can be used.

On the other hand, if processes exhibit Byzantine failures, continuing to run when sick and sending out erroneous or random replies, a minimum of 2k + 1 processors are needed to achieve k fault tolerance. In the worst case, the k failing processes could accidentally (or even intentionally) generate the same reply. However, the remaining k + 1 will also produce the same answer, so the client or voter can just believe the majority.

Of course, in theory it is fine to say that a system is k fault tolerant and just let the k + 1 identical replies outvote the k identical replies, but in practice it is hard to imagine circumstances in which one can say with certainty that k processes can fail but k + 1 processes cannot fail. Thus even in a fault-tolerant system some kind of statistical analysis may be needed.

An implicit precondition for this model to be relevant is that all requests arrive at all servers in the same order, also called the atomic multicast problem. Actually, this condition can be relaxed slightly, since reads do not matter and some writes may commute, but the general problem remains. Atomic multicasting is discussed in detail in a later section.

8.2.3. Agreement in Faulty Systems

Organizing replicated processes into a group helps to increase fault tolerance. As we mentioned, if a client can base its decisions through a voting mechanism, we can even tolerate that k out of 2k + 1 processes are lying about their result. The assumption we are making, however, is that processes do not team up to produce a wrong result.

In general, matters become more intricate if we demand that a process group reaches an agreement, which is needed in many cases. Some examples are: electing a coordinator, deciding whether or not to commit a transaction, dividing up tasks among workers, and synchronization, among numerous other possibilities. When the communication and processes are all perfect, reaching such agreement is often straightforward, but when they are not, problems arise.

[Page 332]

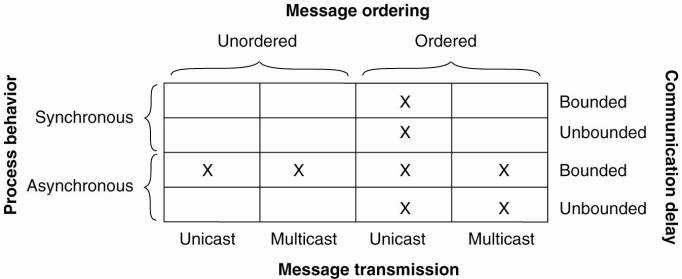
The general goal of distributed agreement algorithms is to have all the nonfaulty processes reach consensus on some issue, and to establish that consensus within a finite number of steps. The problem is complicated by the fact that different assumptions about the underlying system require different solutions, assuming solutions even exist. Turek and Shasha (1992) distinguish the following cases,

1.         Synchronous versus asynchronous systems. A system is synchronous if and only if the processes are known to operate in a lock-step mode. Formally, this means that there should be some constant c  1, such that if any processor has taken c + 1 steps, every other process has taken at least 1 step. A system that is not synchronous is said to be asynchronous.

2.         Communication delay is bounded or not. Delay is bounded if and only if we know that every message is delivered with a globally and predetermined maximum time.

3.         Message delivery is ordered or not. In other words, we distinguish the situation where messages from the same sender are delivered in the order that they were sent, from the situation in which we do not have such guarantees.

4.         Message transmission is done through unicasting or multicasting.

As it turns out, reaching agreement is only possible for the situations shown in Fig. 8-4. In all other cases, it can be shown that no solution exists. Note that most distributed systems in practice assume that processes behave asynchronously, message transmission is unicast, and communication delays are unbounded. As a consequence, we need to make use of ordered (reliable) message delivery, such as provided as by TCP. Fig. 8-4 illustrates the nontrivial nature of distributed agreement when processes may fail.

Figure 8-4. Circumstances under which distributed agreement can be reached.

(This item is displayed on page 333 in the print version)

The problem was originally studied by Lamport et al. (1982) and is also known as the Byzantine agreement problem, referring to the numerous wars in which several armies needed to reach agreement on, for example, troop strengths while being faced with traitorous generals, conniving lieutenants, and so on. Consider the following solution, described in Lamport et al. (1982). In this case, we assume that processes are synchronous, messages are unicast while preserving ordering, and communication delay is bounded. We assume that there are N processes, where each process i will provide a value vi to the others. The goal is let each process construct a vector V of length N, such that if process i is nonfaulty, V [i ] = vi. Otherwise, V [i ] is undefined. We assume that there are at most k faulty processes.

In Fig. 8-5 we illustrate the working of the algorithm for the case of N = 4 and k = 1. For these parameters, the algorithm operates in four steps. In step 1, every nonfaulty process i sends vi to every other process using reliable unicasting. Faulty processes may send anything. Moreover, because we are using multicasting, they may send different values to different processes. Let vi =i. In Fig. 8-5(a) we see that process 1 reports 1, process 2 reports 2, process 3 lies to everyone, giving x, y, and z, respectively, and process 4 reports a value of 4. In step 2, the results of the announcements of step 1 are collected together in the form of the vectors of Fig. 8-5(b).

[Page 333]

Figure 8-5. The Byzantine agreement problem for three nonfaulty and one faulty process. (a) Each process sends their value to the others. (b) The vectors that each process assembles based on (a). (c) The vectors that each process receives in step 3.

[           

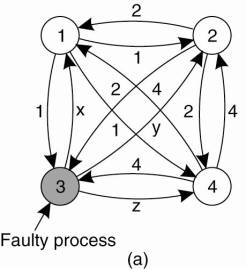
Step 3 consists of every process passing its vector from Fig. 8-5(b) to every other process. In this way, every process gets three vectors, one from every other process. Here, too, process 3 lies, inventing 12 new values, a through l. The results of step 3 are shown in Fig. 8-5(c). Finally, in step 4, each process examines the ith element of each of the newly received vectors. If any value has a majority, that value is put into the result vector. If no value has a majority, the corresponding element of the result vector is marked UNKNOWN. From Fig. 8-5(c) we see that 1, 2, and 4 all come to agreement on the values for v1, v2, and v4, which is the correct result. What these processes conclude regarding v 3 cannot be decided, but is also irrelevant. The goal of Byzantine agreement is that consensus is reached on the value for the nonfaulty processes only.

[Page 334]

Now let us revisit this problem for N = 3 and k = 1, that is, only two nonfaulty process and one faulty one, as illustrated in Fig. 8-6. Here we see that in Fig. 8-6(c) neither of the correctly behaving processes sees a majority for element 1, element 2, or element 3, so all of them are marked UNKNOWN. The algorithm has failed to produce agreement.

Figure 8-6. The same as Fig. 8-5, except now with two correct process and one faulty process.

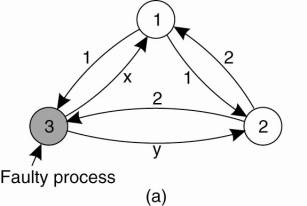
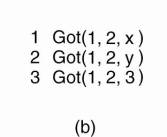
In their paper, Lamport et al. (1982) proved that in a system with k faulty processes, agreement can be achieved only if 2k + 1 correctly functioning processes are present, for a total of 3k + 1. Put in slightly different terms, agreement is possible only if more than two-thirds of the processes are working properly.

Another way of looking at this problem, is as follows. Basically, what we need to achieve is a majority vote among a group of nonfaulty processes regardless of whether there are also faulty ones among their midsts. If there are k faulty processes, we need to ensure that their vote, along with that of any correct process who have been mislead by the faulty ones, still corresponds to the majority vote of the nonfaulty processes. With 2k + 1 nonfaulty processes, this can be achieved by requiring that agreement is reached only if more than two-thirds of the votes are the same. In other words, if more than two-thirds of the processes agree on the same decision, this decision corresponds to the same majority vote by the group of nonfaulty processes.

However, reaching agreement can be even worse. Fischer et al. (1985) proved that in a distributed system in which messages cannot be guaranteed to be delivered within a known, finite time, no agreement is possible if even one process is faulty (albeit if that one process fails silently). The problem with such systems is that arbitrarily slow processes are indistinguishable from crashed ones (i.e., you cannot tell the dead from the living). Many other theoretical results are known about when agreement is possible and when it is not. Surveys of these results are given in Barborak et al. (1993) and Turek and Shasha (1992).

[Page 335]

It should also be noted that the schemes described so far assume that nodes are either Byzantine, or collaborative. The latter cannot always be simply assumed when processes are from different administrative domains. In that case, they will more likely exhibit rational behavior, for example, by reporting timeouts when doing so is cheaper than executing an update operation. How to deal with these cases is not trivial. A first step toward a solution is captured in the form of BAR fault tolerance, which stands for Byzantine, Altruism, and Rationality. BAR fault tolerance is described in Aiyer et al. (2005).

8.2.4. Failure Detection

It may have become clear from our discussions so far that in order to properly mask failures, we generally need to detect them as well. Failure detection is one of the cornerstones of fault tolerance in distributed systems. What it all boils down to is that for a group of processes, nonfaulty members should be able to decide who is still a member, and who is not. In other words, we need to be able to detect when a member has failed.

When it comes to detecting process failures, there are essentially only two mechanisms. Either processes actively send "are you alive?" messages to each other (for which they obviously expect an answer), or passively wait until messages come in from different processes. The latter approach makes sense only when it can be guaranteed that there is enough communication between processes. In practice, actively pinging processes is usually followed.

There has been a huge body of theoretical work on failure detectors. What it all boils down to is that a timeout mechanism is used to check whether a process has failed. In real settings, there are two major problems with this approach. First, due to unreliable networks, simply stating that a process has failed because it does not return an answer to a ping message may be wrong. In other words, it is quite easy to generate false positives. If a false positive has the effect that a perfectly healthy process is removed from a membership list, then clearly we are doing something wrong.

Another serious problem is that timeouts are just plain crude. As noticed by Birman (2005), there is hardly any work on building proper failure detection subsystems that take more into account than only the lack of a reply to a single message. This statement is even more evident when looking at industry-deployed distributed systems.

There are various issues that need to be taken into account when designing a failure detection subsystem [see also Zhuang et al. (2005)]. For example, failure detection can take place through gossiping in which each node regularly announces to its neighbors that it is still up and running. As we mentioned, an alternative is to let nodes actively probe each other.

[Page 336]

Failure detection can also be done as a side-effect of regularly exchanging information with neighbors, as is the case with gossip-based information dissemination (which we discussed in Chap. 4). This approach is essentially also adopted in Obduro (Vogels, 2003): processes periodically gossip their service availability. This information is gradually disseminated through the network by gossiping. Eventually, every process will know about every other process, but more importantly, will have enough information locally available to decide whether a process has failed or not. A member for which the availability information is old, will presumably have failed.

Another important issue is that a failure detection subsystem should ideally be able to distinguish network failures from node failures. One way of dealing with this problem is not to let a single node decide whether one of its neighbors has crashed. Instead, when noticing a timeout on a ping message, a node requests other neighbors to see whether they can reach the presumed failing node. Of course, positive information can also be shared: if a node is still alive, that information can be forwarded to other interested parties (who may be detecting a link failure to the suspected node).

This brings us to another key issue: when a member failure is detected, how should other nonfaulty processes be informed? One simple, and somewhat radical approach is the one followed in FUSE (Dunagan et al., 2004). In FUSE, processes can be joined in a group that spans a wide-area network. The group members create a spanning tree that is used for monitoring member failures. Members send ping messages to their neighbors. When a neighbor does not respond, the pinging node immediately switches to a state in which it will also no longer respond to pings from other nodes. By recursion, it is seen that a single node failure is rapidly promoted to a group failure notification. FUSE does not suffer a lot from link failures for the simple reason that it relies on point-to-point TCP connections between group members.

8.3. Reliable Client-Server Communication

In many cases, fault tolerance in distributed systems concentrates on faulty processes. However, we also need to consider communication failures. Most of the failure models discussed previously apply equally well to communication channels. In particular, a communication channel may exhibit crash, omission, timing, and arbitrary failures. In practice, when building reliable communication channels, the focus is on masking crash and omission failures. Arbitrary failures may occur in the form of duplicate messages, resulting from the fact that in a computer network messages may be buffered for a relatively long time, and are reinjected into the network after the original sender has already issued a retransmission [see, for example, Tanenbaum, 2003)].

8.3.1. Point-to-Point Communication

In many distributed systems, reliable point-to-point communication is established by making use of a reliable transport protocol, such as TCP. TCP masks omission failures, which occur in the form of lost messages, by using acknowledgments and retransmissions. Such failures are completely hidden from a TCP client.

However, crash failures of connections are not masked. A crash failure may occur when (for whatever reason) a TCP connection is abruptly broken so that no more messages can be transmitted through the channel. In most cases, the client is informed that the channel has crashed by raising an exception. The only way to mask such failures is to let the distributed system attempt to automatically set up a new connection, by simply resending a connection request. The underlying assumption is that the other side is still, or again, responsive to such requests.

8.3.2. RPC Semantics in the Presence of Failures

Let us now take a closer look at client-server communication when using high-level communication facilities such as Remote Procedure Calls (RPCs). The goal of RPC is to hide communication by making remote procedure calls look just like local ones. With a few exceptions, so far we have come fairly close. Indeed, as long as both client and server are functioning perfectly, RPC does its job well. The problem comes about when errors occur. It is then that the differences between local and remote calls are not always easy to mask.

To structure our discussion, let us distinguish between five different classes of failures that can occur in RPC systems, as follows:

1. The client is unable to locate the server.

2. The request message from the client to the server is lost.

3. The server crashes after receiving a request.

4. The reply message from the server to the client is lost.

5. The client crashes after sending a request.

Each of these categories poses different problems and requires different solutions.

Client Cannot Locate the Server

To start with, it can happen that the client cannot locate a suitable server. All servers might be down, for example. Alternatively, suppose that the client is compiled using a particular version of the client stub, and the binary is not used for a considerable period of time. In the meantime, the server evolves and a new version of the interface is installed; new stubs are generated and put into use. When the client is eventually run, the binder will be unable to match it up with a server and will report failure. While this mechanism is used to protect the client from accidentally trying to talk to a server that may not agree with it in terms of what parameters are required or what it is supposed to do, the problem remains of how should this failure be dealt with.

[Page 338]

One possible solution is to have the error raise an exception. In some languages, (e.g., Java), programmers can write special procedures that are invoked upon specific errors, such as division by zero. In C, signal handlers can be used for this purpose. In other words, we could define a new signal type SIGNO-SERVER, and allow it to be handled in the same way as other signals.

This approach, too, has drawbacks. To start with, not every language has exceptions or signals. Another point is that having to write an exception or signal handler destroys the transparency we have been trying to achieve. Suppose that you are a programmer and your boss tells you to write the sum procedure. You smile and tell her it will be written, tested, and documented in five minutes. Then she mentions that you also have to write an exception handler as well, just in case the procedure is not there today. At this point it is pretty hard to maintain the illusion that remote procedures are no different from local ones, since writing an exception handler for "Cannot locate server" would be a rather unusual request in a single-processor system. So much for transparency.

Lost Request Messages

The second item on the list is dealing with lost request messages. This is the easiest one to deal with: just have the operating system or client stub start a timer when sending the request. If the timer expires before a reply or acknowledgment comes back, the message is sent again. If the message was truly lost, the server will not be able to tell the difference between the retransmission and the original, and everything will work fine. Unless, of course, so many request messages are lost that the client gives up and falsely concludes that the server is down, in which case we are back to "Cannot locate server." If the request was not lost, the only thing we need to do is let the server be able to detect it is dealing with a retransmission. Unfortunately, doing so is not so simple, as we explain when discussing lost replies.

Server Crashes

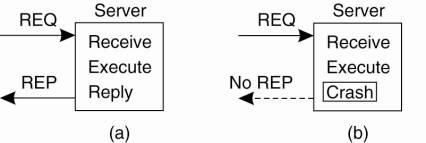
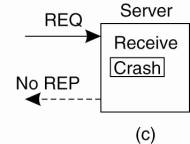
The next failure on the list is a server crash. The normal sequence of events at a server is shown in Fig. 8-7(a). A request arrives, is carried out, and a reply is sent. Now consider Fig. 8-7(b). A request arrives and is carried out, just as before, but the server crashes before it can send the reply. Finally, look at Fig. 8-7(c). Again a request arrives, but this time the server crashes before it can even be carried out. And, of course, no reply is sent back.

Figure 8-7. A server in client-server communication. (a) The normal case. (b) Crash after execution. (c) Crash before execution.

(This item is displayed on page 339 in the print version)

[Page 339]

The annoying part of Fig. 8-7 is that the correct treatment differs for (b) and (c). In (b) the system has to report failure back to the client (e.g., raise an exception), whereas in (c) it can just retransmit the request. The problem is that the client's operating system cannot tell which is which. All it knows is that its timer has expired.

Three schools of thought exist on what to do here (Spector, 1982). One philosophy is to wait until the server reboots (or rebind to a new server) and try the operation again. The idea is to keep trying until a reply has been received, then give it to the client. This technique is called at least once semantics and guarantees that the RPC has been carried out at least one time, but possibly more.

The second philosophy gives up immediately and reports back failure. This way is called at-most-once semantics and guarantees that the RPC has been carried out at most one time, but possibly none at all.

The third philosophy is to guarantee nothing. When a server crashes, the client gets no help and no promises about what happened. The RPC may have been carried out anywhere from zero to a large number of times. The main virtue of this scheme is that it is easy to implement.

None of these are terribly attractive. What one would like is exactly once semantics, but in general, there is no way to arrange this. Imagine that the remote operation consists of printing some text, and that the server sends a completion message to the client when the text is printed. Also assume that when a client issues a request, it receives an acknowledgment that the request has been delivered to the server. There are two strategies the server can follow. It can either send a completion message just before it actually tells the printer to do its work, or after the text has been printed.

Assume that the server crashes and subsequently recovers. It announces to all clients that it has just crashed but is now up and running again. The problem is that the client does not know whether its request to print some text will actually be carried out.

There are four strategies the client can follow. First, the client can decide to never reissue a request, at the risk that the text will not be printed. Second, it can decide to always reissue a request, but this may lead to its text being printed twice. Third, it can decide to reissue a request only if it did not yet receive an acknowledgment that its print request had been delivered to the server. In that case, the client is counting on the fact that the server crashed before the print request could be delivered. The fourth and last strategy is to reissue a request only if it has received an acknowledgment for the print request.

[Page 340]

With two strategies for the server, and four for the client, there are a total of eight combinations to consider. Unfortunately, no combination is satisfactory. To explain, note that there are three events that can happen at the server: send the completion message (M), print the text (P), and crash (C). These events can occur in six different orderings:

1. MPC: A crash occurs after sending the completion message and printing the text.

2. MC (P): A crash happens after sending the completion message, but before the text could be printed.

3. PMC: A crash occurs after sending the completion message and printing the text.

4. PC(M): The text printed, after which a crash occurs before the completion message could be sent.

5. C (PM): A crash happens before the server could do anything.

6. C (MP): A crash happens before the server could do anything.

The parentheses indicate an event that can no longer happen because the server already crashed. Fig. 8-8 shows all possible combinations. As can be readily verified, there is no combination of client strategy and server strategy that will work correctly under all possible event sequences. The bottom line is that the client can never know whether the server crashed just before or after having the text printed.

Figure 8-8. Different combinations of client and server strategies in the presence of server crashes.

[Page 341]

In short, the possibility of server crashes radically changes the nature of RPC and clearly distinguishes single-processor systems from distributed systems. In the former case, a server crash also implies a client crash, so recovery is neither possible nor necessary. In the latter it is both possible and necessary to take action.

Lost Reply Messages

Lost replies can also be difficult to deal with. The obvious solution is just to rely on a timer again that has been set by the client's operating system. If no reply is forthcoming within a reasonable period, just send the request once more. The trouble with this solution is that the client is not really sure why there was no answer. Did the request or reply get lost, or is the server merely slow? It may make a difference.

In particular, some operations can safely be repeated as often as necessary with no damage being done. A request such as asking for the first 1024 bytes of a file has no side effects and can be executed as often as necessary without any harm being done. A request that has this property is said to be idempotent.

Now consider a request to a banking server asking to transfer a million dollars from one account to another. If the request arrives and is carried out, but the reply is lost, the client will not know this and will retransmit the message. The bank server will interpret this request as a new one, and will carry it out too. Two million dollars will be transferred. Heaven forbid that the reply is lost 10 times. Transferring money is not idempotent.

One way of solving this problem is to try to structure all the requests in an idempotent way. In practice, however, many requests (e.g., transferring money) are inherently nonidempotent, so something else is needed. Another method is to have the client assign each request a sequence number. By having the server keep track of the most recently received sequence number from each client that is using it, the server can tell the difference between an original request and a retransmission and can refuse to carry out any request a second time. However, the server will still have to send a response to the client. Note that this approach does require that the server maintains administration on each client. Furthermore, it is not clear how long to maintain this administration. An additional safeguard is to have a bit in the message header that is used to distinguish initial requests from retransmissions (the idea being that it is always safe to perform an original request; retransmissions may require more care).

Client Crashes

The final item on the list of failures is the client crash. What happens if a client sends a request to a server to do some work and crashes before the server replies? At this point a computation is active and no parent is waiting for the result. Such an unwanted computation is called an orphan.

[Page 342]

Orphans can cause a variety of problems that can interfere with normal operation of the system. As a bare minimum, they waste CPU cycles. They can also lock files or otherwise tie up valuable resources. Finally, if the client reboots and does the RPC again, but the reply from the orphan comes back immediately afterward, confusion can result.

What can be done about orphans? Nelson (1981) proposed four solutions. In solution 1, before a client stub sends an RPC message, it makes a log entry telling what it is about to do. The log is kept on disk or some other medium that survives crashes. After a reboot, the log is checked and the orphan is explicitly killed off. This solution is called orphan extermination.

The disadvantage of this scheme is the horrendous expense of writing a disk record for every RPC. Furthermore, it may not even work, since orphans themselves may do RPCs, thus creating grandorphans or further descendants that are difficult or impossible to locate. Finally, the network may be partitioned, due to a failed gateway, making it impossible to kill them, even if they can be located. All in all, this is not a promising approach.

In solution 2, called reincarnation, all these problems can be solved without the need to write disk records. The way it works is to divide time up into sequentially numbered epochs. When a client reboots, it broadcasts a message to all machines declaring the start of a new epoch. When such a broadcast comes in, all remote computations on behalf of that client are killed. Of course, if the network is partitioned, some orphans may survive. Fortunately, however, when they report back, their replies will contain an obsolete epoch number, making them easy to detect.

Solution 3 is a variant on this idea, but somewhat less draconian. It is called gentle reincarnation. When an epoch broadcast comes in, each machine checks to see if it has any remote computations running locally, and if so, tries its best to locate their owners. Only if the owners cannot be located anywhere is the computation killed.

Finally, we have solution 4, expiration, in which each RPC is given a standard amount of time, T, to do the job. If it cannot finish, it must explicitly ask for another quantum, which is a nuisance. On the other hand, if after a crash the client waits a time T before rebooting, all orphans are sure to be gone. The problem to be solved here is choosing a reasonable value of T in the face of RPCs with wildly differing requirements.

In practice, all of these methods are crude and undesirable. Worse yet, killing an orphan may have unforeseen consequences. For example, suppose that an orphan has obtained locks on one or more files or data base records. If the orphan is suddenly killed, these locks may remain forever. Also, an orphan may have already made entries in various remote queues to start up other processes at some future time, so even killing the orphan may not remove all traces of it. Conceivably, it may even started again, with unforeseen consequences. Orphan elimination is discussed in more detail by Panzieri and Shrivastava (1988).

8.4. Reliable Group Communication

Considering how important process resilience by replication is, it is not surprising that reliable multicast services are important as well. Such services guarantee that messages are delivered to all members in a process group. Unfortunately, reliable multicasting turns out to be surprisingly tricky. In this section, we take a closer look at the issues involved in reliably delivering messages to a process group.

8.4.1. Basic Reliable-Multicasting Schemes

Although most transport layers offer reliable point-to-point channels, they rarely offer reliable communication to a collection of processes. The best they can offer is to let each process set up a point-to-point connection to each other process it wants to communicate with. Obviously, such an organization is not very efficient as it may waste network bandwidth. Nevertheless, if the number of processes is small, achieving reliability through multiple reliable point-to-point channels is a simple and often straightforward solution.

To go beyond this simple case, we need to define precisely what reliable multicasting is. Intuitively, it means that a message that is sent to a process group should be delivered to each member of that group. However, what happens if during communication a process joins the group? Should that process also receive the message? Likewise, we should also determine what happens if a (sending) process crashes during communication.

To cover such situations, a distinction should be made between reliable communication in the presence of faulty processes, and reliable communication when processes are assumed to operate correctly. In the first case, multicasting is considered to be reliable when it can be guaranteed that all nonfaulty group members receive the message. The tricky part is that agreement should be reached on what the group actually looks like before a message can be delivered, in addition to various ordering constraints. We return to these matters when we discussw atomic multicasts below.

The situation becomes simpler if we assume agreement exists on who is a member of the group and who is not. In particular, if we assume that processes do not fail, and processes do not join or leave the group while communication is going on, reliable multicasting simply means that every message should be delivered to each current group member. In the simplest case, there is no requirement that all group members receive messages in the same order, but sometimes this feature is needed.

This weaker form of reliable multicasting is relatively easy to implement, again subject to the condition that the number of receivers is limited. Consider the case that a single sender wants to multicast a message to multiple receivers. Assume that the underlying communication system offers only unreliable multicasting, meaning that a multicast message may be lost part way and delivered to some, but not all, of the intended receivers.

[Page 344]

A simple solution is shown in Fig. 8-9. The sending process assigns a sequence number to each message it multicasts. We assume that messages are received in the order they are sent. In this way, it is easy for a receiver to detect it is missing a message. Each multicast message is stored locally in a history buffer at the sender. Assuming the receivers are known to the sender, the sender simply keeps the message in its history buffer until each receiver has returned an acknowledgment. If a receiver detects it is missing a message, it may return a negative acknowledgment, requesting the sender for a retransmission. Alternatively, the sender may automatically retransmit the message when it has not received all acknowledgments within a certain time.

Figure 8-9. A simple solution to reliable multicasting when all receivers are known and are assumed not to fail. (a) Message transmission. (b) Reporting feedback.

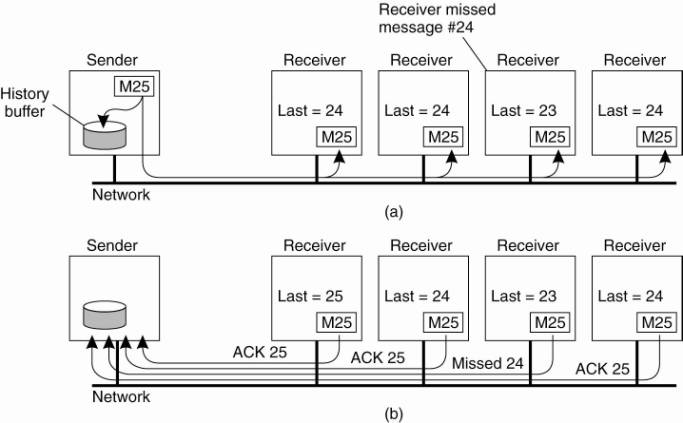
There are various design trade-offs to be made. For example, to reduce the number of messages returned to the sender, acknowledgments could possibly be piggybacked with other messages. Also, retransmitting a message can be done using point-to-point communication to each requesting process, or using a single multicast message sent to all processes. A extensive and detailed survey of total-order broadcasts can be found in Defago et al. (2004).

8.4.2. Scalability in Reliable Multicasting

The main problem with the reliable multicast scheme just described is that it cannot support large numbers of receivers. If there are N receivers, the sender must be prepared to accept at least N acknowledgments. With many receivers, the sender may be swamped with such feedback messages, which is also referred to as a feedback implosion. In addition, we may also need to take into account that the receivers are spread across a wide-area network.

One solution to this problem is not to have receivers acknowledge the receipt of a message. Instead, a receiver returns a feedback message only to inform the sender it is missing a message. Returning only such negative acknowledgments can be shown to generally scale better [see, for example, Towsley et al. (1997)], but no hard guarantees can be given that feedback implosions will never happen.

Another problem with returning only negative acknowledgments is that the sender will, in theory, be forced to keep a message in its history buffer forever. Because the sender can never know if a message has been correctly delivered to all receivers, it should always be prepared for a receiver requesting the retransmission of an old message. In practice, the sender will remove a message from its history buffer after some time has elapsed to prevent the buffer from overflowing. However, removing a message is done at the risk of a request for a retransmission not being honored.

Several proposals for scalable reliable multicasting exist. A comparison between different schemes can be found in Levine and Garcia-Luna-Aceves (1998). We now briefly discuss two very different approaches that are representative of many existing solutions.

Nonhierarchical Feedback Control

The key issue to scalable solutions for reliable multicasting is to reduce the number of feedback messages that are returned to the sender. A popular model that has been applied to several wide-area applications is feedback suppression. This scheme underlies the Scalable Reliable Multicasting (SRM) protocol developed by Floyd et al. (1997) and works as follows.

First, in SRM, receivers never acknowledge the successful delivery of a multicast message, but instead, report only when they are missing a message. How message loss is detected is left to the application. Only negative acknowledgments are returned as feedback. Whenever a receiver notices that it missed a message, it multicasts its feedback to the rest of the group.

Multicasting feedback allows another group member to suppress its own feed-back. Suppose several receivers missed message m. Each of them will need to return a negative acknowledgment to the sender, S, so that m can be retransmitted. However, if we assume that retransmissions are always multicast to the entire group, it is sufficient that only a single request for retransmission reaches S.

[Page 346]

For this reason, a receiver R that did not receive message m schedules a feed-back message with some random delay. That is, the request for retransmission is not sent until some random time has elapsed. If, in the meantime, another request for retransmission for m reaches R, R will suppress its own feedback, knowing that m will be retransmitted shortly. In this way, ideally, only a single feedback message will reach S, which in turn subsequently retransmits m. This scheme is shown in Fig. 8-10.

Figure 8-10. Several receivers have scheduled a request for retransmission, but the first retransmission request leads to the suppression of others.

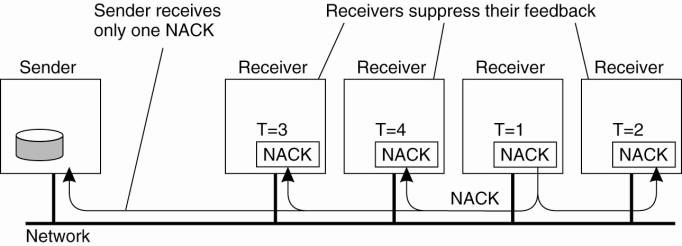
Feedback suppression has shown to scale reasonably well, and has been used as the underlying mechanism for a number of collaborative Internet applications, such as a shared whiteboard. However, the approach also introduces a number of serious problems. First, ensuring that only one request for retransmission is returned to the sender requires a reasonably accurate scheduling of feedback messages at each receiver. Otherwise, many receivers will still return their feedback at the same time. Setting timers accordingly in a group of processes that is dispersed across a wide-area network is not that easy.

Another problem is that multicasting feedback also interrupts those processes to which the message has been successfully delivered. In other words, other receivers are forced to receive and process messages that are useless to them. The only solution to this problem is to let receivers that have not received message m join a separate multicast group for m, as explained in Kasera et al. (1997). Unfortunately, this solution requires that groups can be managed in a highly efficient manner, which is hard to accomplish in a wide-area system. A better approach is therefore to let receivers that tend to miss the same messages team up and share the same multicast channel for feedback messages and retransmissions. Details on this approach are found in Liu et al. (1998).

To enhance the scalability of SRM, it is useful to let receivers assist in local recovery. In particular, if a receiver to which message m has been successfully delivered, receives a request for retransmission, it can decide to multicast m even before the retransmission request reaches the original sender. Further details can be found in Floyd et al. (1997) and Liu et al. (1998).

Hierarchical Feedback Control

Feedback suppression as just described is basically a nonhierarchical solution. However, achieving scalability for very large groups of receivers requires that hierarchical approaches are adopted. In essence, a hierarchical solution to reliable multicasting works as shown in Fig. 8-11.

Figure 8-11. The essence of hierarchical reliable multicasting. Each local coordinator forwards the message to its children and later handles retransmission requests.

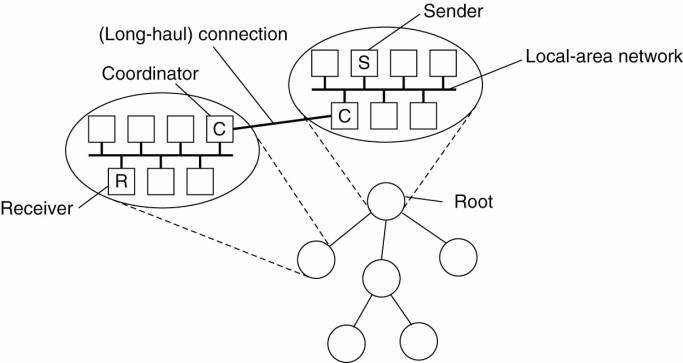
To simplify matters, assume there is only a single sender that needs to multicast messages to a very large group of receivers. The group of receivers is partitioned into a number of subgroups, which are subsequently organized into a tree. The subgroup containing the sender forms the root of the tree. Within each subgroup, any reliable multicasting scheme that works for small groups can be used.

Each subgroup appoints a local coordinator, which is responsible for handling retransmission requests of receivers contained in its subgroup. The local coordinator will thus have its own history buffer. If the coordinator itself has missed a message m, it asks the coordinator of the parent subgroup to retransmit m. In a scheme based on acknowledgments, a local coordinator sends an acknowledgment to its parent if it has received the message. If a coordinator has received acknowledgments for message m from all members in its subgroup, as well as from its children, it can remove m from its history buffer.

The main problem with hierarchical solutions is the construction of the tree. In many cases, a tree needs to be constructed dynamically. One approach is to make use of the multicast tree in the underlying network, if there is one. In principle, the approach is then to enhance each multicast router in the network layer in such a way that it can act as a local coordinator in the way just described. Unfortunately, as a practical matter, such adaptations to existing computer networks are not easy to do. For these reasons, application-level multicasting solutions as we discussed in Chap. 4 have gained popularity.

[Page 348]

In conclusion, building reliable multicast schemes that can scale to a large number of receivers spread across a wide-area network, is a difficult problem. No single best solution exists, and each solution introduces new problems.

8.4.3. Atomic Multicast

Let us now return to the situation in which we need to achieve reliable multicasting in the presence of process failures. In particular, what is often needed in a distributed system is the guarantee that a message is delivered to either all processes or to none at all. In addition, it is generally also required that all messages are delivered in the same order to all processes. This is also known as the atomic multicast problem.

To see why atomicity is so important, consider a replicated database constructed as an application on top of a distributed system. The distributed system offers reliable multicasting facilities. In particular, it allows the construction of process groups to which messages can be reliably sent. The replicated database is therefore constructed as a group of processes, one process for each replica. Update operations are always multicast to all replicas and subsequently performed locally. In other words, we assume that an active-replication protocol is used.

Suppose that now that a series of updates is to be performed, but that during the execution of one of the updates, a replica crashes. Consequently, that update is lost for that replica but on the other hand, it is correctly performed at the other replicas.

When the replica that just crashed recovers, at best it can recover to the same state it had before the crash; however, it may have missed several updates. At that point, it is essential that it is brought up to date with the other replicas. Bringing the replica into the same state as the others requires that we know exactly which operations it missed, and in which order these operations are to be performed.

Now suppose that the underlying distributed system supported atomic multicasting. In that case, the update operation that was sent to all replicas just before one of them crashed is either performed at all nonfaulty replicas, or by none at all. In particular, with atomic multicasting, the operation can be performed by all correctly operating replicas only if they have reached agreement on the group membership. In other words, the update is performed if the remaining replicas have agreed that the crashed replica no longer belongs to the group.

When the crashed replica recovers, it is now forced to join the group once more. No update operations will be forwarded until it is registered as being a member again. Joining the group requires that its state is brought up to date with the rest of the group members. Consequently, atomic multicasting ensures that nonfaulty processes maintain a consistent view of the database, and forces reconciliation when a replica recovers and rejoins the group.

Virtual Synchrony

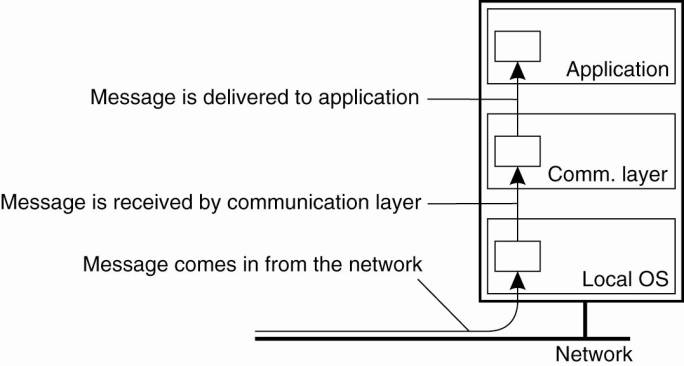
Reliable multicast in the presence of process failures can be accurately defined in terms of process groups and changes to group membership. As we did earlier, we make a distinction between receiving and delivering a message. In particular, we again adopt a model in which the distributed system consists of a communication layer, as shown in Fig. 8-12. Within this communication layer, messages are sent and received. A received message is locally buffered in the communication layer until it can be delivered to the application that is logically placed at a higher layer.

Figure 8-12. The logical organization of a distributed system to distinguish between message receipt and message delivery.

The whole idea of atomic multicasting is that a multicast message m is uniquely associated with a list of processes to which it should be delivered. This delivery list corresponds to a group view, namely, the view on the set of processes contained in the group, which the sender had at the time message m was multicast. An important observation is that each process on that list has the same view. In other words, they should all agree that m should be delivered to each one of them and to no other process.

Now suppose that the message m is multicast at the time its sender has group view G. Furthermore, assume that while the multicast is taking place, another process joins or leaves the group. This change in group membership is naturally announced to all processes in G. Stated somewhat differently, a view change takes place by multicasting a message vc announcing the joining or leaving of a process. We now have two multicast messages simultaneously in transit: m and vc. What we need to guarantee is that m is either delivered to all processes in G before each one of them is delivered message vc, or m is not delivered at all. Note that this requirement is somewhat comparable to totally-ordered multicasting, which we discussed in Chap. 6.

[Page 350]

A question that quickly comes to mind is that if m is not delivered to any process, how can we speak of a reliable multicast protocol? In principle, there is only one case in which delivery of m is allowed to fail: when the group membership change is the result of the sender of m crashing. In that case, either all members of G should hear the abort of the new member, or none. Alternatively, m may be ignored by each member, which corresponds to the situation that the sender crashed before m was sent.

This stronger form of reliable multicast guarantees that a message multicast to group view G is delivered to each nonfaulty process in G. If the sender of the message crashes during the multicast, the message may either be delivered to all remaining processes, or ignored by each of them. A reliable multicast with this property is said to be virtually synchronous (Birman and Joseph, 1987).

Consider the four processes shown in Fig. 8-13. At a certain point in time, process P1 joins the group, which then consists of P1, P2, P3, and P4. After some messages have been multicast, P3 crashes. However, before crashing, it succeeded in multicasting a message to process P2 and P4, but not to P1. However, virtual synchrony guarantees that the message is not delivered at all, effectively establishing the situation that the message was never sent before P3 crashed.

Figure 8-13. The principle of virtual synchronous multicast.

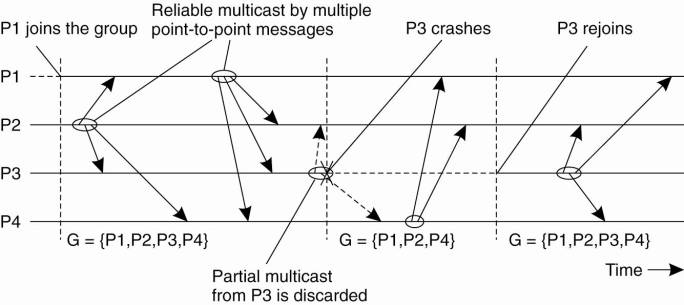
After P3 has been removed from the group, communication proceeds between the remaining group members. Later, when P3 recovers, it can join the group again, after its state has been brought up to date.

The principle of virtual synchrony comes from the fact that all multicasts take place between view changes. Put somewhat differently, a view change acts as a barrier across which no multicast can pass. In a sense, it is comparable to the use of a synchronization variable in distributed data stores as discussed in the previous chapter. All multicasts that are in transit while a view change takes place are completed before the view change comes into effect. The implementation of virtual synchrony is not trivial as we will discuss in detail below.

Message Ordering

Virtual synchrony allows an application developer to think about multicasts as taking place in epochs that are separated by group membership changes. However, nothing has yet been said concerning the ordering of multicasts. In general, four different orderings are distinguished:

1. Unordered multicasts

2. FIFO-ordered multicasts

3. Causally-ordered multicasts

4. Totally-ordered multicasts

A reliable, unordered multicast is a virtually synchronous multicast in which no guarantees are given concerning the order in which received messages are delivered by different processes. To explain, assume that reliable multicasting is supported by a library providing a send and a receive primitive. The receive operation blocks the calling process until a message is delivered to it.

Now suppose a sender P1 multicasts two messages to a group while two other processes in that group are waiting for messages to arrive, as shown in Fig. 8-14. Assuming that processes do not crash or leave the group during these multicasts, it is possible that the communication layer at P2 first receives message m1 and then m 2. Because there are no message-ordering constraints, the messages may be delivered to P2 in the order that they are received. In contrast, the communication layer at P3 may first receive message m 2 followed by m 1, and delivers these two in this same order to P3.

Figure 8-14. Three communicating processes in the same group. The ordering of events per process is shown along the vertical axis.Process

In the case of reliable FIFO-ordered multicasts, the communication layer is forced to deliver incoming messages from the same process in the same order as they have been sent. Consider the communication within a group of four processes, as shown in Fig. 8-15. With FIFO ordering, the only thing that matters is that message m 1 is always delivered before m 2, and, likewise, that message m 3 is always delivered before m 4 . This rule has to be obeyed by all processes in the group. In other words, when the communication layer at P3 receives m 2 first, it will wait with delivery to P3 until it has received and delivered m 1.

[Page 352]

Figure 8-15. Four processes in the same group with two different senders, and a possible delivery order of messages under FIFO-ordered multicasting.

However, there is no constraint regarding the delivery of messages sent by different processes. In other words, if process P2 receives m 1 before m 3, it may deliver the two messages in that order. Meanwhile, process P3 may have received m 3 before receiving m 1. FIFO ordering states that P3 may deliver m 3 before m 1, although this delivery order is different from that of P2.

Finally, reliable causally-ordered multicast delivers messages so that potential causality between different messages is preserved. In other words, if a message m 1 causally precedes another message m 2, regardless of whether they were multicast by the same sender, then the communication layer at each receiver will always deliver m 2 after it has received and delivered m 1. Note that causally-ordered multicasts can be implemented using vector timestamps as discussed in Chap. 6.

Besides these three orderings, there may be the additional constraint that message delivery is to be totally ordered as well. Total-ordered delivery means that regardless of whether message delivery is unordered, FIFO ordered, or causally ordered, it is required additionally that when messages are delivered, they are delivered in the same order to all group members.

For example, with the combination of FIFO and totally-ordered multicast, processes P2 and P3 in Fig. 8-15 may both first deliver message m 3 and then message m 1. However, if P2 delivers m 1 before m 3, while P3 delivers m 3 before delivering m 1, they would violate the total-ordering constraint. Note that FIFO ordering should still be respected. In other words, m 2 should be delivered after m 1 and, accordingly, m 4 should be delivered after m 3.

Virtually synchronous reliable multicasting offering totally-ordered delivery of messages is called atomic multicasting. With the three different message ordering constraints discussed above, this leads to six forms of reliable multicasting as shown in Fig. 8-16 (Hadzilacos and Toueg, 1993).

Figure 8-16. Six different versions of virtually synchronous reliable multicasting.

(This item is displayed on page 353 in the print version)

Implementing Virtual Synchrony

Let us now consider a possible implementation of a virtually synchronous reliable multicast. An example of such an implementation appears in Isis, a fault-tolerant distributed system that has been in practical use in industry for several years. We will focus on some of the implementation issues of this technique as described in Birman et al. (1991).

[Page 353]

Reliable multicasting in Isis makes use of available reliable point-to-point communication facilities of the underlying network, in particular, TCP. Multicasting a message m to a group of processes is implemented by reliably sending m to each group member. As a consequence, although each transmission is guaranteed to succeed, there are no guarantees that all group members receive m. In particular, the sender may fail before having transmitted m to each member.

Besides reliable point-to-point communication, Isis also assumes that messages from the same source are received by a communication layer in the order they were sent by that source. In practice, this requirement is solved by using TCP connections for point-to-point communication.

The main problem that needs to be solved is to guarantee that all messages sent to view G are delivered to all nonfaulty processes in G before the next group membership change takes place. The first issue that needs to be taken care of is making sure that each process in G has received all messages that were sent to G. Note that because the sender of a message m to G may have failed before completing its multicast, there may indeed be processes in G that will never receive m. Because the sender has crashed, these processes should get m from somewhere else. How a process detects it is missing a message is explained next.

The solution to this problem is to let every process in G keep m until it knows for sure that all members in G have received it. If m has been received by all members in G, m is said to be stable. Only stable messages are allowed to be delivered. To ensure stability, it is sufficient to select an arbitrary (operational) process in G and request it to send m to all other processes.

To be more specific, assume the current view is Gi, but that it is necessary to install the next view Gi+1 . Without loss of generality, we may assume that Gi and Gi+1 differ by at most one process. A process P notices the view change when it receives a view-change message. Such a message may come from the process wanting to join or leave the group, or from a process that had detected the failure of a process in Gi that is now to be removed, as shown in Fig. 8-17(a).

Figure 8-17. (a) Process 4 notices that process 7 has crashed and sends a view change. (b) Process 6 sends out all its unstable messages, followed by a flush message. (c) Process 6 installs the new view when it has received a flush message from everyone else.

(This item is displayed on page 354 in the print version)

[Page 354]

When a process P receives the view-change message for Gi+1, it first forwards a copy of any unstable message from Gi it still has to every process in Gi+1, and subsequently marks it as being stable. Recall that Isis assumes point-to-point communication is reliable, so that forwarded messages are never lost. Such forwarding guarantees that all messages in Gi that have been received by at least one process are received by all nonfaulty processes in Gi. Note that it would also have been sufficient to elect a single coordinator to forward unstable messages.

To indicate that P no longer has any unstable messages and that it is prepared to install Gi+1 as soon as the other processes can do that as well, it multicasts a flush message for Gi+1, as shown in Fig. 8-17(b). After P has received a flush message for Gi+1 from each other process, it can safely install the new view [shown in Fig. 8-17(c)].

When a process Q receives a message m that was sent in Gi, and Q still believes the current view is Gi, it delivers m taking any additional message-ordering constraints into account. If it had already received m, it considers the message to be a duplicate and further discards it.

Because process Q will eventually receive the view-change message for Gi+1, it will also first forward any of its unstable messages and subsequently wrap things up by sending a flush message for Gi+1. Note that due to the message ordering underlying the communication layer, a flush message from a process is always received after the receipt of an unstable message from that same process.

The major flaw in the protocol described so far is that it cannot deal with process failures while a new view change is being announced. In particular, it assumes that until the new view Gi+1 has been installed by each member in Gi+1, no process in Gi+1 will fail (which would lead to a next view Gi+2 ). This problem is solved by announcing view changes for any view Gi+k even while previous changes have not yet been installed by all processes. The details are left as an exercise for the reader.

8.5. Distributed Commit

The atomic multicasting problem discussed in the previous section is an example of a more general problem, known as distributed commit. The distributed commit problem involves having an operation being performed by each member of a process group, or none at all. In the case of reliable multicasting, the operation is the delivery of a message. With distributed transactions, the operation may be the commit of a transaction at a single site that takes part in the transaction. Other examples of distributed commit, and how it can be solved are discussed in Tanisch (2000).

Distributed commit is often established by means of a coordinator. In a simple scheme, this coordinator tells all other processes that are also involved, called participants, whether or not to (locally) perform the operation in question. This scheme is referred to as a one-phase commit protocol. It has the obvious drawback that if one of the participants cannot actually perform the operation, there is no way to tell the coordinator. For example, in the case of distributed transactions, a local commit may not be possible because this would violate concurrency control constraints.

In practice, more sophisticated schemes are needed, the most common one being the two-phase commit protocol, which is discussed in detail below. The main drawback of this protocol is that it cannot efficiently handle the failure of the coordinator. To that end, a three-phase protocol has been developed, which we also discuss.

8.5.1. Two-Phase Commit

The original two-phase commit protocol (2PC) is due to Gray (1978) Without loss of generality, consider a distributed transaction involving the participation of a number of processes each running on a different machine. Assuming that no failures occur, the protocol consists of the following two phases, each consisting of two steps [see also Bernstein et al. (1987)]:

1.         The coordinator sends a VOTE_REQUEST message to all participants.

2.         When a participant receives a VOTE_REQUEST message, it returns either a VOTE_COMMIT message to the coordinator telling the coordinator that it is prepared to locally commit its part of the transaction, or otherwise a VOTE_ABORT message.

3.         The coordinator collects all votes from the participants. If all participants have voted to commit the transaction, then so will the coordinator. In that case, it sends a GLOBAL_COMMIT message to all participants. However, if one participant had voted to abort the transaction, the coordinator will also decide to abort the transaction and multicasts a GLOBAL_ABORT message.

4.         Each participant that voted for a commit waits for the final reaction by the coordinator. If a participant receives a GLOBAL_COMMIT message, it locally commits the transaction. Otherwise, when receiving a GLOBAL_ABORT message, the transaction is locally aborted as well.

The first phase is the voting phase, and consists of steps 1 and 2. The second phase is the decision phase, and consists of steps 3 and 4. These four steps are shown as finite state diagrams in Fig. 8-18.

Figure 8-18. (a) The finite state machine for the coordinator in 2PC. (b) The finite state machine for a participant.

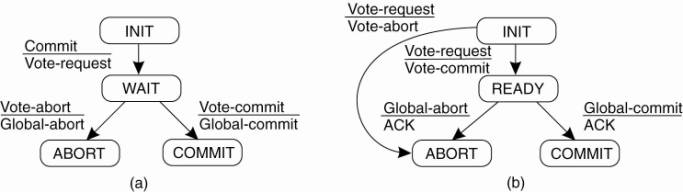
Several problems arise when this basic 2PC protocol is used in a system where failures occur. First, note that the coordinator as well as the participants have states in which they block waiting for incoming messages. Consequently, the protocol can easily fail when a process crashes for other processes may be indefinitely waiting for a message from that process. For this reason, timeout mechanism are used. These mechanisms are explained in the following pages.

When taking a look at the finite state machines in Fig. 8-18, it can be seen that there are a total of three states in which either a coordinator or participant is blocked waiting for an incoming message. First, a participant may be waiting in its INIT state for a VOTE_REQUEST message from the coordinator. If that message is not received after some time, the participant will simply decide to locally abort the transaction, and thus send a VOTE_ABORT message to the coordinator.

Likewise, the coordinator can be blocked in state WAIT, waiting for the votes of each participant. If not all votes have been collected after a certain period of time, the coordinator should vote for an abort as well, and subsequently send GLOBAL_ABORT to all participants.

[Page 357]

Finally, a participant can be blocked in state READY, waiting for the global vote as sent by the coordinator. If that message is not received within a given time, the participant cannot simply decide to abort the transaction. Instead, it must find out which message the coordinator actually sent. The simplest solution to this problem is to let each participant block until the coordinator recovers again.

A better solution is to let a participant P contact another participant Q to see if it can decide from Q's current state what it should do. For example, suppose that Q had reached state COMMIT. This is possible only if the coordinator had sent a GLOBAL_COMMIT message to Q just before crashing. Apparently, this message had not yet been sent to P. Consequently, P may now also decide to locally commit. Likewise, if Q is in state ABORT, P can safely abort as well.

Now suppose that Q is still in state INIT. This situation can occur when the coordinator has sent a VOTE_REQUEST to all participants, but this message has reached P (which subsequently responded with a VOTE_COMMIT message), but has not reached Q. In other words, the coordinator had crashed while multicasting VOTE_REQUEST. In this case, it is safe to abort the transaction: both P and Q can make a transition to state ABORT.

The most difficult situation occurs when Q is also in state READY, waiting for a response from the coordinator. In particular, if it turns out that all participants are in state READY, no decision can be taken. The problem is that although all participants are willing to commit, they still need the coordinator's vote to reach the final decision. Consequently, the protocol blocks until the coordinator recovers.

The various options are summarized in Fig. 8-19.

Figure 8-19. Actions taken by a participant P when residing in state READY and having contacted another participant Q.

To ensure that a process can actually recover, it is necessary that it saves its state to persistent storage. (How saving data can be done in a fault-tolerant way is discussed later in this chapter.) For example, if a participant was in state INIT, it can safely decide to locally abort the transaction when it recovers, and then inform the coordinator. Likewise, when it had already taken a decision such as when it crashed while being in either state COMMIT or ABORT, it is in order to recover to that state again, and retransmit its decision to the coordinator.

[Page 358]

Problems arise when a participant crashed while residing in state READY. In that case, when recovering, it cannot decide on its own what it should do next, that is, commit or abort the transaction. Consequently, it is forced to contact other participants to find what it should do, analogous to the situation when it times out while residing in state READY as described above.

The coordinator has only two critical states it needs to keep track of. When it starts the 2PC protocol, it should record that it is entering state WAIT so that it can possibly retransmit the VOTE_REQUEST message to all participants after recovering. Likewise, if it had come to a decision in the second phase, it is sufficient if that decision has been recorded so that it can be retransmitted when recovering.

An outline of the actions that are executed by the coordinator is given in Fig. 8-20. The coordinator starts by multicasting a VOTE_REQUEST to all participants in order to collect their votes. It subsequently records that it is entering the WAIT state, after which it waits for incoming votes from participants.

Figure 8-20. Outline of the steps taken by the coordinator in a two-phase commit protocol.

If not all votes have been collected but no more votes are received within a given time interval prescribed in advance, the coordinator assumes that one or more participants have failed. Consequently, it should abort the transaction and multicasts a GLOBAL_ABORT to the (remaining) participants.

[Page 359]

If no failures occur, the coordinator will eventually have collected all votes. If all participants as well as the coordinator vote to commit, GLOBAL_COMMIT is first logged and subsequently sent to all processes. Otherwise, the coordinator multicasts a GLOBAL_ABORT (after recording it in the local log).

Fig. 8-21(a) shows the steps taken by a participant. First, the process waits for a vote request from the coordinator. Note that this waiting can be done by a separate thread running in the process's address space. If no message comes in, the transaction is simply aborted. Apparently, the coordinator had failed.

After receiving a vote request, the participant may decide to vote for committing the transaction for which it first records its decision in a local log, and then informs the coordinator by sending a VOTE_COMMIT message. The participant must then wait for the global decision. Assuming this decision (which again should come from the coordinator) comes in on time, it is simply written to the local log, after which it can be carried out.

However, if the participant times out while waiting for the coordinator's decision to come in, it executes a termination protocol by first multicasting a DECISION_REQUEST message to the other processes, after which it subsequently blocks while waiting for a response. When a response comes in (possibly from the coordinator, which is assumed to eventually recover), the participant writes the decision to its local log and handles it accordingly.

Each participant should be prepared to accept requests for a global decision from other participants. To that end, assume each participant starts a separate thread, executing concurrently with the main thread of the participant as shown in Fig. 8-21(b). This thread blocks until it receives a decision request. It can only be of help to anther process if its associated participant has already reached a final decision. In other words, if GLOBAL_COMMIT or GLOBAL_ABORT had been written to the local log, it is certain that the coordinator had at least sent its decision to this process. In addition, the thread may also decide to send a GLOBAL_ABORT when its associated participant is still in state INIT, as discussed previously. In all other cases, the receiving thread cannot help, and the requesting participant will not be responded to.

What is seen is that it may be possible that a participant will need to block until the coordinator recovers. This situation occurs when all participants have received and processed the VOTE_REQUEST from the coordinator, while in the meantime, the coordinator crashed. In that case, participants cannot cooperatively decide on the final action to take. For this reason, 2PC is also referred to as a blocking commit protocol.

There are several solutions to avoid blocking. One solution, described by Babaoglu and Toueg (1993), is to use a multicast primitive by which a receiver immediately multicasts a received message to all other processes. It can be shown that this approach allows a participant to reach a final decision, even if the coordinator has not yet recovered. Another solution is the three-phase commit protocol, which is the last topic of this section and is discussed next.

[Page 360]

Figure 8-21. (a) The steps taken by a participant process in 2PC. (b) The steps for handling incoming decision requests.

8.5.2. Three-Phase Commit

A problem with the two-phase commit protocol is that when the coordinator has crashed, participants may not be able to reach a final decision. Consequently, participants may need to remain blocked until the coordinator recovers. Skeen (1981) developed a variant of 2PC, called the three-phase commit protocol (3PC), that avoids blocking processes in the presence of fail-stop crashes. Although 3PC is widely referred to in the literature, it is not applied often in practice as the conditions under which 2PC blocks rarely occur. We discuss the protocol, as it provides further insight into solving fault-tolerance problems in distributed systems.

Like 2PC, 3PC is also formulated in terms of a coordinator and a number of participants. Their respective finite state machines are shown in Fig. 8-22. The essence of the protocol is that the states of the coordinator and each participant satisfy the following two conditions:

There is no single state from which it is possible to make a transition directly to either a COMMIT or an ABORT state.

There is no state in which it is not possible to make a final decision, and from which a transition to a COMMIT state can be made.

Figure 8-22. (a) The finite state machine for the coordinator in 3PC. (b) The finite state machine for a participant.

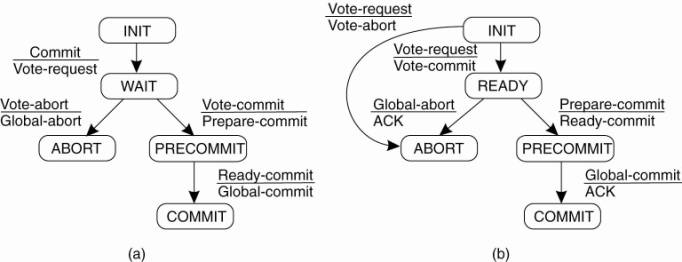
It can be shown that these two conditions are necessary and sufficient for a commit protocol to be nonblocking (Skeen and Stonebraker, 1983).

The coordinator in 3PC starts with sending a VOTE_REQUEST message to all participants, after which it waits for incoming responses. If any participant votes to abort the transaction, the final decision will be to abort as well, so the coordinator sends GLOBAL_ABORT. However, when the transaction can be committed, a PREPARE_COMMIT message is sent. Only after each participant has acknowledged it is now prepared to commit, will the coordinator send the final GLOBAL_COMMIT message by which the transaction is actually committed.

[Page 362]

Again, there are only a few situations in which a process is blocked while waiting for incoming messages. First, if a participant is waiting for a vote request from the coordinator while residing in state INIT, it will eventually make a transition to state ABORT, thereby assuming that the coordinator has crashed. This situation is identical to that in 2PC. Analogously, the coordinator may be in state WAIT, waiting for the votes from participants. On a timeout, the coordinator will conclude that a participant crashed, and will thus abort the transaction by multicasting a GLOBAL_ABORT message.

Now suppose the coordinator is blocked in state PRECOMMIT. On a timeout, it will conclude that one of the participants had crashed, but that participant is known to have voted for committing the transaction. Consequently, the coordinator can safely instruct the operational participants to commit by multicasting a GLOBAL_COMMIT message. In addition, it relies on a recovery protocol for the crashed participant to eventually commit its part of the transaction when it comes up again.

A participant P may block in the READY state or in the PRECOMMIT state. On a timeout, P can conclude only that the coordinator has failed, so that it now needs to find out what to do next. As in 2PC, if P contacts any other participant that is in state COMMIT (or ABORT), P should move to that state as well. In addition, if all participants are in state PRECOMMIT, the transaction can be safely committed.

Again analogous to 2PC, if another participant Q is still in the INIT state, the transaction can safely be aborted. It is important to note that Q can be in state INIT only if no other participant is in state PRECOMMIT. A participant can reach PRECOMMIT only if the coordinator had reached state PRECOMMIT before crashing, and has thus received a vote to commit from each participant. In other words, no participant can reside in state INIT while another participant is in state PRECOMMIT.

If each of the participants that P can contact is in state READY (and they together form a majority), the transaction should be aborted. The point to note is that another participant may have crashed and will later recover. However, neither P, nor any other of the operational participants knows what the state of the crashed participant will be when it recovers. If the process recovers to state INIT, then deciding to abort the transaction is the only correct decision. At worst, the process may recover to state PRECOMMIT, but in that case, it cannot do any harm to still abort the transaction.

This situation is the major difference with 2PC, where a crashed participant could recover to a COMMIT state while all the others were still in state READY. In that case, the remaining operational processes could not reach a final decision and would have to wait until the crashed process recovered. With 3PC, if any operational process is in its READY state, no crashed process will recover to a state other than INIT, ABORT, or PRECOMMIT. For this reason, surviving processes can always come to a final decision.

[Page 363]

Finally, if the processes that P can reach are in state PRECOMMIT (and they form a majority), then it is safe to commit the transaction. Again, it can be shown that in this case, all other processes will either be in state READY or at least, will recover to state READY, PRECOMMIT, or COMMIT when they had crashed.

Further details on 3PC can be found in Bernstein et al. (1987) and Chow and Johnson (1997).

8.6. Recovery

So far, we have mainly concentrated on algorithms that allow us to tolerate faults. However, once a failure has occurred, it is essential that the process where the failure happened can recover to a correct state. In what follows, we first concentrate on what it actually means to recover to a correct state, and subsequently when and how the state of a distributed system can be recorded and recovered to, by means of checkpointing and message logging.

8.6.1. Introduction

Fundamental to fault tolerance is the recovery from an error. Recall that an error is that part of a system that may lead to a failure. The whole idea of error recovery is to replace an erroneous state with an error-free state. There are essentially two forms of error recovery.

In backward recovery, the main issue is to bring the system from its present erroneous state back into a previously correct state. To do so, it will be necessary to record the system's state from time to time, and to restore such a recorded state when things go wrong. Each time (part of) the system's present state is recorded, a checkpoint is said to be made.

Another form of error recovery is forward recovery. In this case, when the system has entered an erroneous state, instead of moving back to a previous, checkpointed state, an attempt is made to bring the system in a correct new state from which it can continue to execute. The main problem with forward error recovery mechanisms is that it has to be known in advance which errors may occur. Only in that case is it possible to correct those errors and move to a new state.

The distinction between backward and forward error recovery is easily explained when considering the implementation of reliable communication. The common approach to recover from a lost packet is to let the sender retransmit that packet. In effect, packet retransmission establishes that we attempt to go back to a previous, correct state, namely the one in which the packet that was lost is being sent. Reliable communication through packet retransmission is therefore an example of applying backward error recovery techniques.

[Page 364]

An alternative approach is to use a method known as erasure correction. In this approach, a missing packet is constructed from other, successfully delivered packets. For example, in an (n,k) block erasure code, a set of k source packets is encoded into a set of n encoded packets, such that any set of k encoded packets is enough to reconstruct the original k source packets. Typical values are k=16 or k = 32, and k<n2k [see, for example, Rizzo (1997)]. If not enough packets have yet been delivered, the sender will have to continue transmitting packets until a previously lost packet can be constructed. Erasure correction is a typical example of a forward error recovery approach.

By and large, backward error recovery techniques are widely applied as a general mechanism for recovering from failures in distributed systems. The major benefit of backward error recovery is that it is a generally applicable method independent of any specific system or process. In other words, it can be integrated into (the middleware layer) of a distributed system as a general-purpose service.

However, backward error recovery also introduces some problems (Singhal and Shivaratri, 1994). First, restoring a system or process to a previous state is generally a relatively costly operation in terms of performance. As will be discussed in succeeding sections, much work generally needs to be done to recover from, for example, a process crash or site failure. A potential way out of this problem, is to devise very cheap mechanisms by which components are simply rebooted. We will return to this approach below.

Second, because backward error recovery mechanisms are independent of the distributed application for which they are actually used, no guarantees can be given that once recovery has taken place, the same or similar failure will not happen again. If such guarantees are needed, handling errors often requires that the application gets into the loop of recovery. In other words, full-fledged failure transparency can generally not be provided by backward error recovery mechanisms.

Finally, although backward error recovery requires checkpointing, some states can simply never be rolled back to. For example, once a (possibly malicious) person has taken the $1,000 that suddenly came rolling out of the incorrectly functioning automated teller machine, there is only a small chance that money will be stuffed back in the machine. Likewise, recovering to a previous state in most UNIX systems after having enthusiastically typed

rm -fr*

but from the wrong working directory, may turn a few people pale. Some things are simply irreversible.

Checkpointing allows the recovery to a previous correct state. However, taking a checkpoint is often a costly operation and may have a severe performance penalty. As a consequence, many fault-tolerant distributed systems combine checkpointing with message logging. In this case, after a checkpoint has been taken, a process logs its messages before sending them off (called sender-based logging). An alternative solution is to let the receiving process first log an incoming message before delivering it to the application it is executing. This scheme is also referred to as receiver-based logging. When a receiving process crashes, it is necessary to restore the most recently checkpointed state, and from there on replay the messages that have been sent. Consequently, combining checkpoints with message logging makes it possible to restore a state that lies beyond the most recent checkpoint without the cost of checkpointing.

[Page 365]

Another important distinction between checkpointing and schemes that additionally use logs follows. In a system where only checkpointing is used, processes will be restored to a checkpointed state. From there on, their behavior may be different than it was before the failure occurred. For example, because communication times are not deterministic, messages may now be delivered in a different order, in turn leading to different reactions by the receivers. However, if message logging takes place, an actual replay of the events that happened since the last checkpoint takes place. Such a replay makes it easier to interact with the outside world.

For example, consider the case that a failure occurred because a user provided erroneous input. If only checkpointing is used, the system would have to take a checkpoint before accepting the user's input in order to recover to exactly the same state. With message logging, an older checkpoint can be used, after which a replay of events can take place up to the point that the user should provide input. In practice, the combination of having fewer checkpoints and message logging is more efficient than having to take many checkpoints.

Stable Storage

To be able to recover to a previous state, it is necessary that information needed to enable recovery is safely stored. Safely in this context means that recovery information survives process crashes and site failures, but possibly also various storage media failures. Stable storage plays an important role when it comes to recovery in distributed systems. We discuss it briefly here.

Storage comes in three categories. First there is ordinary RAM memory, which is wiped out when the power fails or a machine crashes. Next there is disk storage, which survives CPU failures but which can be lost in disk head crashes.

Finally, there is also stable storage, which is designed to survive anything except major calamities such as floods and earthquakes. Stable storage can be implemented with a pair of ordinary disks, as shown in Fig. 8-23(a). Each block on drive 2 is an exact copy of the corresponding block on drive 1. When a block is updated, first the block on drive 1 is updated and verified, then the same block on drive 2 is done.

Figure 8-23. (a) Stable storage. (b) Crash after drive 1 is updated. (c) Bad spot.

(This item is displayed on page 366 in the print version)

Suppose that the system crashes after drive 1 is updated but before the update on drive 2, as shown in Fig. 8-23(b). Upon recovery, the disk can be compared block for block. Whenever two corresponding blocks differ, it can be assumed that drive 1 is the correct one (because drive 1 is always updated before drive 2), so the new block is copied from drive 1 to drive 2. When the recovery process is complete, both drives will again be identical.

[Page 366]

Another potential problem is the spontaneous decay of a block. Dust particles or general wear and tear can give a previously valid block a sudden checksum error, without cause or warning, as shown in Fig. 8-23(c). When such an error is detected, the bad block can be regenerated from the corresponding block on the other drive.

As a consequence of its implementation, stable storage is well suited to applications that require a high degree of fault tolerance, such as atomic transactions. When data are written to stable storage and then read back to check that they have been written correctly, the chance of them subsequently being lost is extremely small.

In the next two sections we go into further details concerning checkpoints and message logging. Elnozahy et al. (2002) provide a survey of checkpointing and logging in distributed systems. Various algorithmic details can be found in Chow and Johnson (1997).

8.6.2. Checkpointing

In a fault-tolerant distributed system, backward error recovery requires that the system regularly saves its state onto stable storage. In particular, we need to record a consistent global state, also called a distributed snapshot. In a distributed snapshot, if a process P has recorded the receipt of a message, then there should also be a process Q that has recorded the sending of that message. After all, it must have come from somewhere.

[Page 367]

In backward error recovery schemes, each process saves its state from time to time to a locally-available stable storage. To recover after a process or system failure requires that we construct a consistent global state from these local states. In particular, it is best to recover to the most recent distributed snapshot, also referred to as a recovery line. In other words, a recovery line corresponds to the most recent consistent collection of checkpoints, as shown in Fig. 8-24.

Figure 8-24. A recovery line.

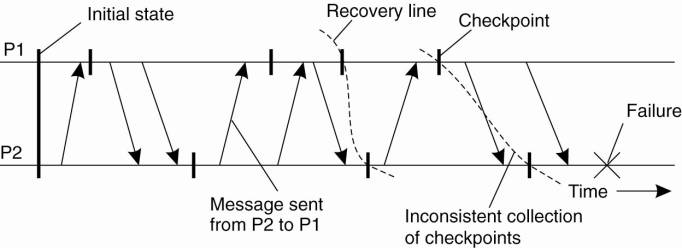
Independent Checkpointing

Unfortunately, the distributed nature of checkpointing (in which each process simply records its local state from time to time in an uncoordinated fashion) may make it difficult to find a recovery line. To discover a recovery line requires that each process is rolled back to its most recently saved state. If these local states jointly do not form a distributed snapshot, further rolling back is necessary. Below, we will describe a way to find a recovery line. This process of a cascaded rollback may lead to what is called the domino effect and is shown in Fig. 8-25.

Figure 8-25. The domino effect.

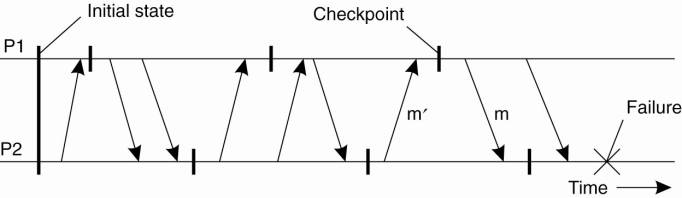
When process P2 crashes, we need to restore its state to the most recently saved checkpoint. As a consequence, process P1 will also need to be rolled back. Unfortunately, the two most recently saved local states do not form a consistent global state: the state saved by P2 indicates the receipt of a message m, but no other process can be identified as its sender. Consequently, P2 needs to be rolled back to an earlier state.

[Page 368]

However, the next state to which P2 is rolled back also cannot be used as part of a distributed snapshot. In this case, P1 will have recorded the receipt of message m', but there is no recorded event of this message being sent. It is therefore necessary to also roll P1 back to a previous state. In this example, it turns out that the recovery line is actually the initial state of the system.

As processes take local checkpoints independent of each other, this method is also referred to as independent checkpointing. An alternative solution is to globally coordinate checkpointing, as we discuss below, but coordination requires global synchronization, which may introduce performance problems. Another disadvantage of independent checkpointing is that each local storage needs to be cleaned up periodically, for example, by running a special distributed garbage collector. However, the main disadvantage lies in computing the recovery line.

Implementing independent checkpointing requires that dependencies are recorded in such a way that processes can jointly roll back to a consistent global state. To that end, let CPi(m) denote the m-th checkpoint taken by process Pi. Also, let INTi(m) denote the interval between checkpoints CPi(m-1) and CPi(m).

When process Pi sends a message in interval INTi(m), it piggybacks the pair (i,m) to the receiving process. When process Pj receives a message in interval INTj(n), along with the pair of indices (i,m), it then records the dependency INTi(m)INTj(n). Whenever Pj takes checkpoint CPj(n), it additionally writes this dependency to its local stable storage, along with the rest of the recovery information that is part of CPj(n).

Now suppose that at a certain moment, process P1 is required to roll back to checkpoint CPi(m-1). To ensure global consistency, we need to ensure that all processes that have received messages from Pi and were sent in interval INTi(m), are rolled back to a checkpointed state preceding the receipt of such messages. In particular, process Pj in our example, will need to be rolled back at least to checkpoint CPj(n-1). If CPj(n-1) does not lead to a globally consistent state, further rolling back may be necessary.

Calculating the recovery line requires an analysis of the interval dependencies recorded by each process when a checkpoint was taken. Without going into any further details, it turns out that such calculations are fairly complex and do not justify the need for independent checkpointing in comparison to coordinated checkpointing. In addition, as it turns out, it is often not the coordination between processes that is the dominating performance factor, but the overhead as the result of having to save the state to local stable storage. Therefore, coordinated checkpointing, which is much simpler than independent checkpointing, is often more popular, and will presumably stay so even when systems grow to much larger sizes (Elnozahy and Planck, 2004).

]

Coordinated Checkpointing

As its name suggests, in coordinated checkpointing all processes synchronize to jointly write their state to local stable storage. The main advantage of coordinated checkpointing is that the saved state is automatically globally consistent, so that cascaded rollbacks leading to the domino effect are avoided. The distributed snapshot algorithm discussed in Chap. 6 can be used to coordinate checkpointing. This algorithm is an example of nonblocking checkpoint coordination.

A simpler solution is to use a two-phase blocking protocol. A coordinator first multicasts a CHECKPOINT_REQUEST message to all processes. When a process receives such a message, it takes a local checkpoint, queues any subsequent message handed to it by the application it is executing, and acknowledges to the coordinator that it is has taken a checkpoint. When the coordinator has received an acknowledgment from all processes, it multicasts a CHECKPOINT_DONE message to allow the (blocked) processes to continue.

It is easy to see that this approach will also lead to a globally consistent state, because no incoming message will ever be registered as part of a checkpoint. The reason for this is that any message that follows a request for taking a checkpoint is not considered to be part of the local checkpoint. At the same time, outgoing messages (as handed to the checkpointing process by the application it is running), are queued locally until the CHECKPOINT_DONE message is received.

An improvement to this algorithm is to multicast a checkpoint request only to those processes that depend on the recovery of the coordinator, and ignore the other processes. A process is dependent on the coordinator if it has received a message that is directly or indirectly causally related to a message that the coordinator had sent since the last checkpoint. This leads to the notion of an incremental snapshot.

To take an incremental snapshot, the coordinator multicasts a checkpoint request only to those processes it had sent a message to since it last took a checkpoint. When a process P receives such a request, it forwards the request to all those processes to which P itself had sent a message since the last checkpoint, and so on. A process forwards the request only once. When all processes have been identified, a second multicast is used to actually trigger checkpointing and to let the processes continue where they had left off.

8.6.3. Message Logging

Considering that checkpointing is an expensive operation, especially concerning the operations involved in writing state to stable storage, techniques have been sought to reduce the number of checkpoints, but still enable recovery. An important technique in distributed systems is logging messages.

The basic idea underlying message logging is that if the transmission of messages can be replayed, we can still reach a globally consistent state but without having to restore that state from stable storage. Instead, a checkpointed state is taken as a starting point, and all messages that have been sent since are simply retransmitted and handled accordingly.

[Page 370]

This approach works fine under the assumption of what is called a piecewise deterministic model. In such a model, the execution of each process is assumed to take place as a series of intervals in which events take place. These events are the same as those discussed in the context of Lamport's happened-before relationship in Chap. 6. For example, an event may be the execution of an instruction, the sending of a message, and so on. Each interval in the piecewise deterministic model is assumed to start with a nondeterministic event, such as the receipt of a message. However, from that moment on, the execution of the process is completely deterministic. An interval ends with the last event before a nondeterministic event occurs.

In effect, an interval can be replayed with a known result, that is, in a completely deterministic way, provided it is replayed starting with the same nondeter-ministic event as before. Consequently, if we record all nondeterministic events in such a model, it becomes possible to completely replay the entire execution of a process in a deterministic way.

Considering that message logs are necessary to recover from a process crash so that a globally consistent state is restored, it becomes important to know precisely when messages are to be logged. Following the approach described by Alvisi and Marzullo (1998), it turns out that many existing message-logging schemes can be easily characterized, if we concentrate on how they deal with orphan processes.

An orphan process is a process that survives the crash of another process, but whose state is inconsistent with the crashed process after its recovery. As an example, consider the situation shown in Fig. 8-26. Process Q receives messages m1 and m2 from process P and R, respectively, and subsequently sends a message m3 to R. However, in contrast to all other messages, message m2 is not logged. If process Q crashes and later recovers again, only the logged messages required for the recovery of Q are replayed, in our example, m1. Because m2 was not logged, its transmission will not be replayed, meaning that the transmission of m3 also may not take place. Fig. 8-26.

Figure 8-26. Incorrect replay of messages after recovery, leading to an orphan process.

(This item is displayed on page 371 in the print version)

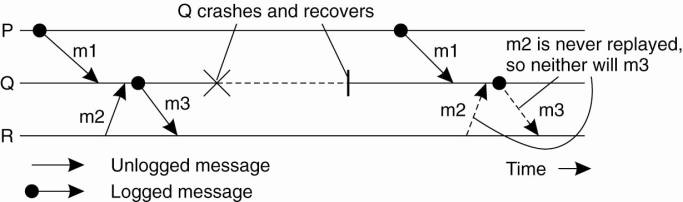
However, the situation after the recovery of Q is inconsistent with that before its recovery. In particular, R holds a message (m3 ) that was sent before the crash, but whose receipt and delivery do not take place when replaying what had happened before the crash. Such inconsistencies should obviously be avoided.

Characterizing Message-Logging Schemes

To characterize different message-logging schemes, we follow the approach described in Alvisi and Marzullo (1998). Each message m is considered to have a header that contains all information necessary to retransmit m, and to properly handle it. For example, each header will identify the sender and the receiver, but also a sequence number to recognize it as a duplicate. In addition, a delivery number may be added to decide when exactly it should be handed over to the receiving application.

[Page 371]

A message is said to be stable if it can no longer be lost, for example, because it has been written to stable storage. Stable messages can thus be used for recovery by replaying their transmission.

Each message m leads to a set DEP (m) of processes that depend on the delivery of m. In particular, DEP (m) consists of those processes to which m has been delivered. In addition, if another message m' is causally dependent on the delivery of m, and m' has been delivered to a process Q, then Q will also be contained in DEP (m). Note that m' is causally dependent on the delivery of m, if it were sent by the same process that previously delivered m, or which had delivered another message that was causally dependent on the delivery of m.

The set COPY (m) consists of those processes that have a copy of m, but not (yet) in their local stable storage. When a process Q delivers message m, it also becomes a member of COPY (m). Note that COPY (m) consists of those processes that could hand over a copy of m that can be used to replay the transmission of m. If all these processes crash, replaying the transmission of m is clearly not feasible.

Using these notations, it is now easy to define precisely what an orphan process is. Suppose that in a distributed system some processes have just crashed. Let Q be one of the surviving processes. Process Q is an orphan process if there is a message m, such that Q is contained in DEP (m), while at the same time every process in COPY (m) has crashed. In other words, an orphan process appears when it is dependent on m, but there is no way to replay m's transmission.

To avoid orphan processes, we thus need to ensure that if each process in COPY (m) crashed, then no surviving process is left in DEP (m). In other words, all processes in DEP (m) should have crashed as well. This condition can be enforced if we can guarantee that whenever a process becomes a member of DEP (m), it also becomes a member of COPY (m). In other words, whenever a process becomes dependent on the delivery of m, it will always keep a copy of m.

[Page 372]

There are essentially two approaches that can now be followed. The first approach is represented by what are called pessimistic logging protocols. These protocols take care that for each nonstable message m, there is at most one process dependent on m. In other words, pessimistic logging protocols ensure that each nonstable message m is delivered to at most one process. Note that as soon as m is delivered to, say process P, P becomes a member of COPY (m).

The worst that can happen is that process P crashes without m ever having been logged. With pessimistic logging, P is not allowed to send any messages after the delivery of m without first having ensured that m has been written to stable storage. Consequently, no other processes will ever become dependent on the delivery of m to P, without having the possibility of replaying the transmission of m. In this way, orphan processes are always avoided.

In contrast, in an optimistic logging protocol, the actual work is done after a crash occurs. In particular, assume that for some message m, each process in COPY (m) has crashed. In an optimistic approach, any orphan process in DEP (m) is rolled back to a state in which it no longer belongs to DEP (m). Clearly, optimistic logging protocols need to keep track of dependencies, which complicates their implementation.

As pointed out in Elnozahy et al. (2002), pessimistic logging is so much simpler than optimistic approaches, that it is the preferred way of message logging in practical distributed systems design.

8.6.4. Recovery-Oriented Computing

A related way of handling recovery is essentially to start over again. The underlying principle toward this way of masking failures is that it may be much cheaper to optimize for recovery, then it is aiming for systems that are free from failures for a long time. This approach is also referred to as recovery-oriented computing (Candea et al., 2004a).

There are different flavors of recovery-oriented computing. One flavor is to simply reboot (part of a system) and has been explored to restart Internet servers (Candea et al., 2004b, 2006). In order to be able reboot only a part of the system, it is crucial the fault is properly localized. At that point, rebooting simply means deleting all instances of the identified components, along with the threads operating on them, and (often) to just restart the associated requests. Note that fault localization itself may be a nontrivial exercise (Steinder and Sethi, 2004).

To enable rebooting as a practical recovery technique requires that components are largely decoupled in the sense that there are few or no dependencies between different components. If there are strong dependencies, then fault localization and analysis may still require that a complete server needs to be restarted at which point applying traditional recovery techniques as the ones we just discussed may be more efficient.

[Page 373]

Another flavor of recovery-oriented computing is to apply checkpointing and recovery techniques, but to continue execution in a changed environment. The basic idea here is that many failures can be simply avoided if programs are given some more buffer space, memory is zeroed before allocated, changing the ordering of message delivery (as long as this does not affect semantics), and so on (Qin et al., 2005). The key idea is to tackle software failures (whereas many of the techniques discussed so far are aimed at, or are based on hardware failures). Because software execution is highly deterministic, changing an execution environment may save the day, but, of course, without repairing anything.