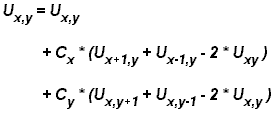|
Introduction to Parallel Computing
|
|
| Author: Blaise Barney, Lawrence Livermore National Laboratory |
UCRL-MI-133316 |
Table of Contents
- Abstract
- Overview
- What is Parallel Computing?
- Why Use Parallel Computing?
- Concepts and Terminology
- von Neumann Computer Architecture
- Flynn's Classical Taxonomy
- Some General Parallel Terminology
- Parallel Computer Memory Architectures
- Shared Memory
- Distributed Memory
- Hybrid Distributed-Shared Memory
- Parallel Programming Models
- Overview
- Shared Memory Model
- Threads Model
- Distributed Memory / Message Passing Model
- Data Parallel Model
- Hybrid Model
- SPMD and MPMP
- Designing Parallel Programs
- Automatic vs. Manual Parallelization
- Understand the Problem and the Program
- Partitioning
- Communications
- Synchronization
- Data Dependencies
- Load Balancing
- Granularity
- I/O
- Limits and Costs of Parallel Programming
- Performance Analysis and Tuning
- Parallel Examples
- Array Processing
- PI Calculation
- Simple Heat Equation
- 1-D Wave Equation
- References and More Information
This tutorial is the first of eight tutorials in the 4+ day "Using
LLNL's Supercomputers" workshop. It is intended to provide only a very
quick overview of the extensive and broad topic of Parallel Computing,
as a lead-in for the tutorials that follow it. As such, it covers just
the very basics of parallel computing, and is intended for someone who
is just becoming acquainted with the subject and who is planning to
attend one or more of the other tutorials in this workshop. It is not
intended to cover Parallel Programming in depth, as this would require
significantly more time. The tutorial begins with a discussion on
parallel computing - what it is and how it's used, followed by a
discussion on concepts and terminology associated with parallel
computing. The topics of parallel memory architectures and programming
models are then explored. These topics are followed by a series of
practical discussions on a number of the complex issues related to
designing and running parallel programs. The tutorial concludes with
several examples of how to parallelize simple serial programs.
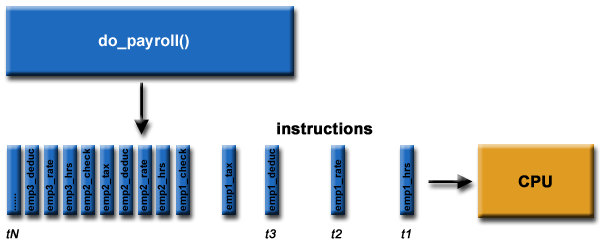
What is Parallel Computing?
- Traditionally, software has been written for serial
computation:
- To be run on a single computer having a single Central Processing
Unit (CPU);
- A problem is broken into a discrete series of instructions.
- Instructions are executed one after another.
- Only one instruction may execute at any moment in time.
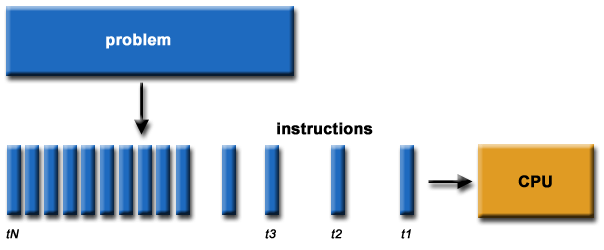
For example:
- In the simplest sense, parallel computing is the simultaneous
use of multiple compute resources to solve a computational problem:
- To be run using multiple CPUs
- A problem is broken into discrete parts that can be solved concurrently
- Each part is further broken down to a series of instructions
- Instructions from each part execute simultaneously on different CPUs
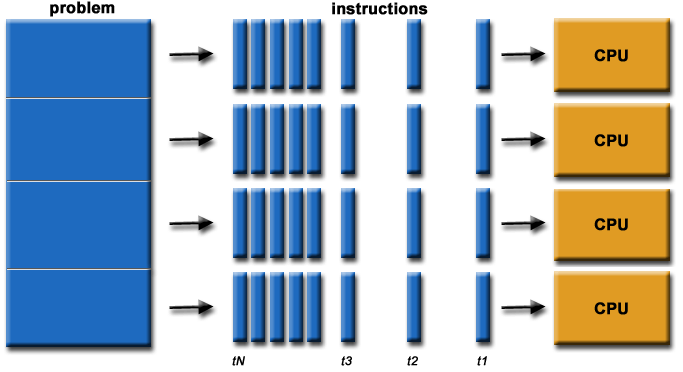
For example:
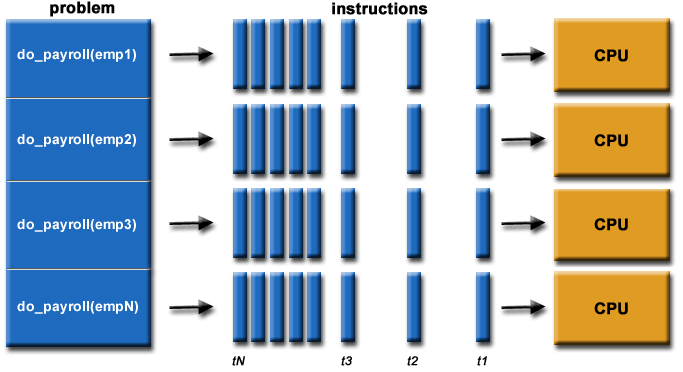
- The compute resources might be:
- A single computer with multiple processors;
- An arbitrary number of computers connected by a network;
- A combination of both.
- The computational problem should be able to:
- Be broken apart into discrete pieces of work that can be solved
simultaneously;
- Execute multiple program instructions at any moment in time;
- Be solved in less time with multiple compute resources than with a single
compute resource.
 The Universe is Parallel:
The Universe is Parallel:
 Uses for Parallel Computing:
Uses for Parallel Computing:
- Science and Engineering:
Historically, parallel computing has been considered to be
"the high end of computing", and has been used to model difficult
problems in many areas of science and engineering:
- Atmosphere, Earth, Environment
- Physics - applied, nuclear, particle, condensed matter,
high pressure, fusion, photonics
- Bioscience, Biotechnology, Genetics
- Chemistry, Molecular Sciences
|
- Geology, Seismology
- Mechanical Engineering - from prosthetics to spacecraft
- Electrical Engineering, Circuit Design, Microelectronics
- Computer Science, Mathematics
|

- Industrial and Commercial:
Today, commercial applications provide an equal or greater driving
force in the development of faster computers.
These applications require the processing of large
amounts of data in sophisticated ways. For example:
- Databases, data mining
- Oil exploration
- Web search engines, web based business services
- Medical imaging and diagnosis
- Pharmaceutical design
|
- Financial and economic modeling
- Management of national and multi-national corporations
- Advanced graphics and virtual reality, particularly in the entertainment industry
- Networked video and multi-media technologies
- Collaborative work environments
|

Why Use Parallel Computing?
 Main Reasons:
Main Reasons:
- Save time and/or money: In theory, throwing more resources at a task
will shorten its time to completion, with potential cost savings. Parallel
computers can be built from cheap, commodity components.
|
 |
- Solve larger problems: Many problems are so large and/or complex that
it is impractical or impossible to solve them on a single computer,
especially given limited computer memory. For example:
- "Grand Challenge" (en.wikipedia.org/wiki/Grand_Challenge) problems requiring
PetaFLOPS and PetaBytes of computing resources.
- Web search engines/databases processing millions of transactions per
second
|
 |
- Provide concurrency: A single compute resource can only do one thing
at a time. Multiple computing resources can be doing many things
simultaneously. For example, the Access Grid
(www.accessgrid.org)
provides a global collaboration network where people from around the
world can meet and conduct work "virtually".
|
 |
- Use of non-local resources: Using compute resources on a wide area
network, or even the Internet when local compute resources are scarce.
For example:
|
 |
- Limits to serial computing: Both physical and practical reasons pose
significant constraints to simply building ever faster serial computers:
- Transmission speeds - the speed of a serial computer is directly
dependent upon how fast data can move through hardware.
Absolute limits are the speed of light (30 cm/nanosecond) and the
transmission limit of copper wire (9 cm/nanosecond). Increasing
speeds necessitate increasing proximity of processing elements.
- Limits to miniaturization - processor technology is allowing an
increasing number of transistors to be placed on a chip. However,
even with molecular
or atomic-level components, a limit will be reached on how small
components can be.
- Economic limitations - it is increasingly expensive to make a single
processor faster. Using a larger number of moderately fast
commodity processors to
achieve the same (or better) performance is less expensive.
- Current computer architectures are increasingly relying upon hardware
level parallelism to improve performance:
- Multiple execution units
- Pipelined instructions
- Multi-core
|
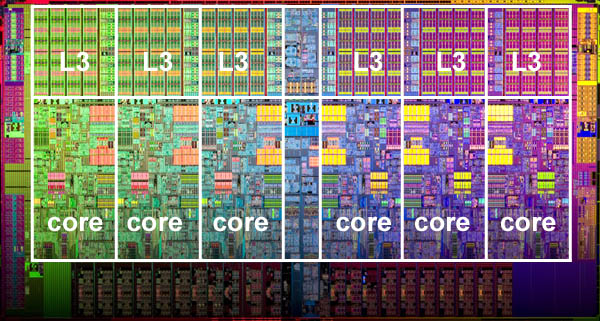 |
 Who and What?
Who and What?
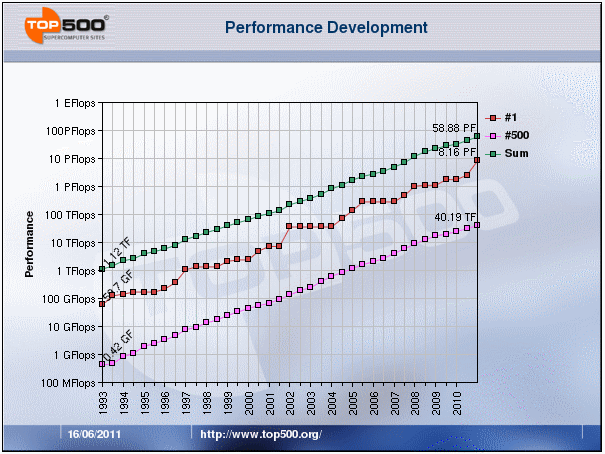
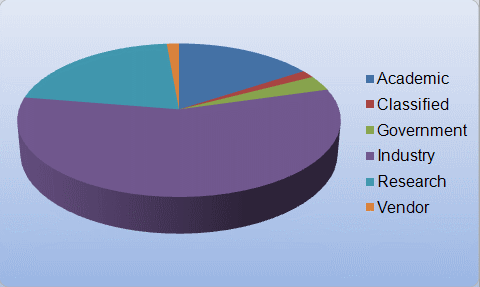
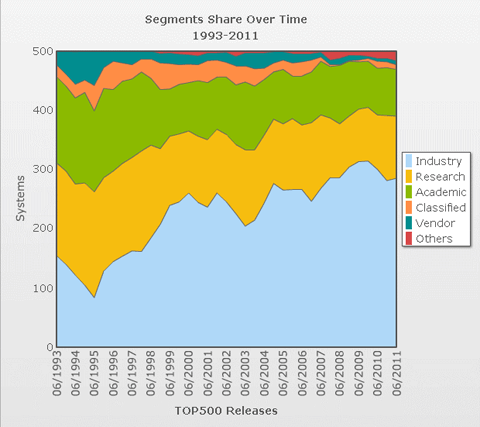
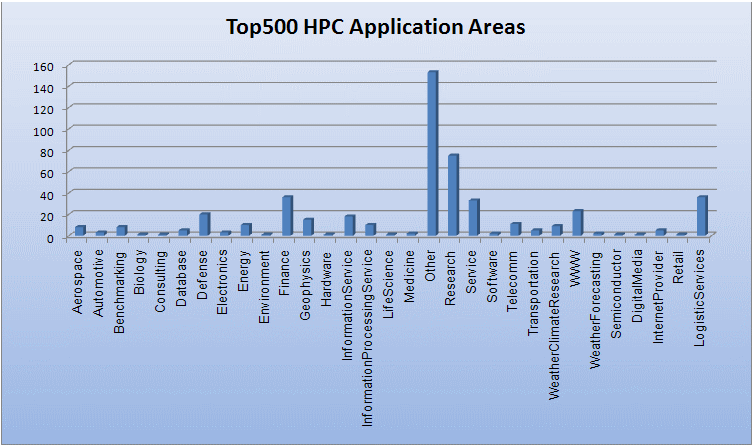
- Top500.org provides statistics on parallel computing - the charts below are just a sampling.
 The Future:
The Future:
- During the past 20+ years, the trends indicated by ever faster
networks, distributed systems, and multi-processor computer architectures
(even at the desktop level) clearly show
that parallelism is the future of computing.
- In this same time period, there has been a greater than 1000x increase in
supercomputer performance, with no end currently in sight.
- The race is already on for Exascale Computing!
von Neumann Architecture
- Named after the Hungarian mathematician John von Neumann who first authored
the general requirements for an electronic computer in his 1945 papers.
- Since then, virtually all computers have followed this basic design,
differing from earlier computers which were programmed through "hard wiring".
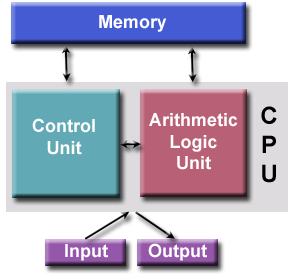 |
- Comprised of four main components:
- Memory
- Control Unit
- Arithmetic Logic Unit
- Input/Output
- Read/write, random access memory is used to store both program instructions
and data
- Program instructions are coded data which tell the computer to do
something
- Data is simply information to be used by the program
- Control unit fetches instructions/data from memory, decodes
the instructions and then sequentially coordinates operations
to accomplish the programmed task.
- Aritmetic Unit performs basic arithmetic operations
- Input/Output is the interface to the human operator
|
- So what? Who cares? Well, parallel computers still follow this basic design,
just multiplied in units. The basic, fundamental architecture remains the same.
Flynn's Classical Taxonomy
- There are different ways to classify parallel computers. One of the more
widely used classifications, in use since 1966, is called Flynn's Taxonomy.
- Flynn's taxonomy distinguishes multi-processor computer architectures
according
to how they can be classified along the two independent dimensions of
Instruction and Data. Each of these dimensions
can have only one of two possible states: Single or
Multiple.
- The matrix below defines the 4 possible classifications according to Flynn:
S I S D
Single Instruction, Single Data |
S I M D
Single Instruction, Multiple Data |
M I S D
Multiple Instruction, Single Data |
M I M D
Multiple Instruction, Multiple Data |
 Single Instruction, Single Data (SISD):
Single Instruction, Single Data (SISD):
- A serial (non-parallel) computer
- Single Instruction: Only one instruction stream is
being acted on by the CPU during any one clock cycle
- Single Data: Only one data stream is being used as input during any one clock cycle
- Deterministic execution
- This is the oldest and even today, the most common type of computer
- Examples: older generation mainframes, minicomputers and workstations;
most modern day PCs.
|
 |

UNIVAC1 |

IBM 360 |

CRAY1 |

CDC 7600 |

PDP1 |

Dell Laptop |
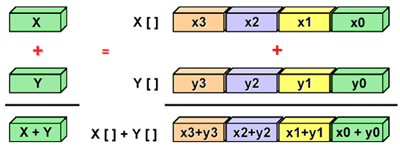
 Single Instruction, Multiple Data (SIMD):
Single Instruction, Multiple Data (SIMD):
- A type of parallel computer
- Single Instruction: All processing units execute the same instruction at any given clock cycle
- Multiple Data: Each processing unit can operate on a different data
element
- Best suited for specialized problems characterized by a high degree of
regularity, such as graphics/image processing.
- Synchronous (lockstep) and deterministic execution
- Two varieties: Processor Arrays and Vector Pipelines
- Examples:
- Processor Arrays: Connection Machine CM-2, MasPar MP-1 & MP-2,
ILLIAC IV
- Vector Pipelines: IBM 9000, Cray X-MP, Y-MP & C90, Fujitsu VP, NEC SX-2,
Hitachi S820, ETA10
- Most modern computers, particularly those with graphics processor units
(GPUs) employ SIMD instructions and execution units.
|
|

Cray X-MP |

Cray Y-MP |

Thinking Machines CM-2 |

Cell Processor (GPU) |
 Multiple Instruction, Single Data (MISD):
Multiple Instruction, Single Data (MISD):
- A type of parallel computer
- Multiple Instruction: Each processing unit operates on the data
independently via separate instruction streams.
- Single Data: A single data stream is fed into multiple processing units.
- Few actual examples of this class of parallel computer have ever existed.
One is the experimental Carnegie-Mellon C.mmp computer (1971).
- Some conceivable uses might be:
- multiple frequency filters operating on a single signal stream
- multiple cryptography algorithms attempting to crack a single coded
message.
|
|
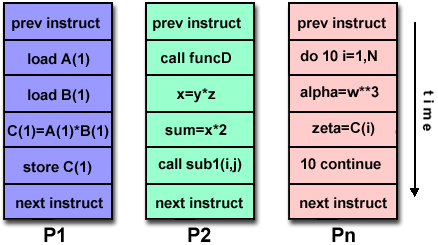
 Multiple Instruction, Multiple Data (MIMD):
Multiple Instruction, Multiple Data (MIMD):
- A type of parallel computer
- Multiple Instruction: Every processor may be executing a different
instruction stream
- Multiple Data: Every processor may be working with a different data
stream
- Execution can be synchronous or asynchronous, deterministic or
non-deterministic
- Currently, the most common type of parallel computer - most modern
supercomputers fall into this category.
- Examples: most current supercomputers, networked parallel computer
clusters and "grids", multi-processor SMP computers, multi-core PCs.
- Note: many MIMD architectures also include SIMD execution sub-components
|
|

IBM POWER5 |

HP/Compaq Alphaserver |

Intel IA32 |

AMD Opteron |

Cray XT3 |

IBM BG/L |
Some General Parallel Terminology
Like everything else, parallel computing has its own "jargon". Some of the
more commonly used terms associated with parallel computing are listed below.
Most of these will be discussed in more detail later.
- Supercomputing / High Performance Computing (HPC)
- Using the world's fastest and largest computers to solve large problems.
- Node
- A standalone "computer in a box". Usually comprised of multiple
CPUs/processors/cores. Nodes are networked together to comprise a
supercomputer.
- CPU / Socket / Processor / Core
- This varies, depending upon who you talk to. In the past, a CPU
(Central Processing Unit) was a singular execution component for a
computer. Then, multiple CPUs were incorporated into a node. Then,
individual CPUs were subdivided into multiple "cores", each being a
unique execution unit. CPUs with multiple cores are sometimes called
"sockets" - vendor dependent. The result is a node with multiple CPUs,
each containing multiple cores. The nomenclature is confused at times.
Wonder why?

- Task
- A logically discrete section of computational work. A task is typically a
program or program-like set of instructions that is executed by a processor.
A parallel program consists of multiple tasks running on multiple processors.
- Pipelining
- Breaking a task into steps performed by different processor
units, with inputs streaming through, much like an assembly line; a type
of parallel computing.
- Shared Memory
- From a strictly hardware point of view, describes a computer architecture
where all processors have direct (usually bus based) access to common
physical memory. In a programming sense, it describes a model where
parallel tasks all have the same "picture" of memory and can directly
address and access the same logical memory locations regardless
of where the physical memory actually exists.
- Symmetric Multi-Processor (SMP)
- Hardware architecture where multiple processors share a single
address space and access to all resources; shared memory computing.
- Distributed Memory
- In hardware, refers to network based memory access for physical memory that
is not common. As a programming model, tasks can only logically "see"
local machine memory and must use communications to access memory on other
machines where other tasks are executing.
- Communications
- Parallel tasks typically need to exchange data. There are
several ways this can be accomplished, such as through a shared memory
bus or over a network, however the actual event of data exchange is
commonly referred to as communications regardless of the method
employed.
- Synchronization
- The coordination of parallel tasks in real time, very often
associated with
communications. Often implemented by establishing a synchronization
point within an application where a task may not proceed further until
another task(s) reaches the same or logically equivalent point.
Synchronization usually involves waiting by at least one task, and can
therefore cause a parallel application's wall clock execution time to
increase.
- Granularity
- In parallel computing, granularity is a qualitative measure of the ratio
of computation to communication.
- Coarse: relatively large amounts of computational work
are done between communication events
- Fine: relatively small amounts of computational work are
done between communication events
- Observed Speedup
- Observed speedup of a code which has been parallelized, defined as:
wall-clock time of serial execution
-----------------------------------
wall-clock time of parallel execution |
One of the simplest and most widely used indicators for a parallel program's performance.
- Parallel Overhead
- The amount of time required to coordinate parallel tasks, as opposed to
doing useful work. Parallel overhead can include factors such as:
- Task start-up time
- Synchronizations
- Data communications
- Software overhead imposed by parallel compilers, libraries, tools,
operating system, etc.
- Task termination time
- Massively Parallel
- Refers to the hardware that comprises a given parallel system -
having many processors. The meaning of "many" keeps increasing, but
currently, the largest
parallel computers can be comprised of processors numbering in the
hundreds of thousands.
- Embarrassingly Parallel
- Solving many similar, but independent tasks
simultaneously; little to no need for coordination between the tasks.
- Scalability
- Refers to a parallel system's (hardware and/or software)
ability to demonstrate a proportionate increase in parallel speedup with
the addition of more processors. Factors that contribute to scalability
include:
- Hardware - particularly memory-cpu bandwidths and network communications
- Application algorithm
- Parallel overhead related
- Characteristics of your specific application and coding
|
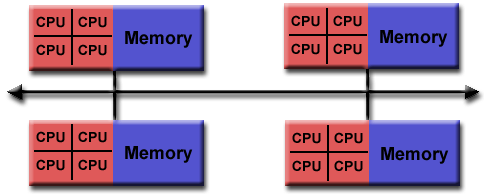
Parallel Computer Memory Architectures |
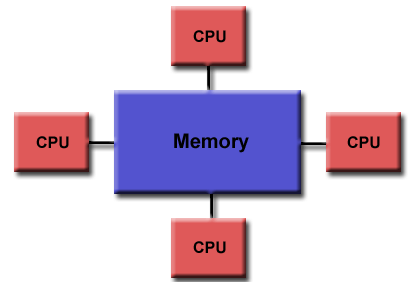
Shared Memory
 General Characteristics:
General Characteristics:
- Shared memory parallel computers vary widely, but generally have in common
the ability for all processors to access all memory as global address space.
- Multiple processors can operate independently but share the same memory
resources.
- Changes in a memory location effected by one processor are visible to all
other processors.
- Shared memory machines can be divided into two main classes based upon
memory access times: UMA and NUMA.
 Uniform Memory Access (UMA):
Uniform Memory Access (UMA):
- Most commonly represented today by Symmetric Multiprocessor (SMP)
machines
- Identical processors
- Equal access and access times to memory
- Sometimes called CC-UMA - Cache Coherent UMA.
Cache coherent means if one processor updates a location in shared
memory, all
the other processors know about the update. Cache coherency is
accomplished at the hardware level.
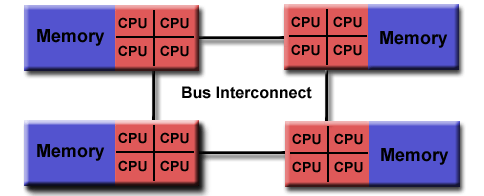
 Non-Uniform Memory Access (NUMA):
Non-Uniform Memory Access (NUMA):
- Often made by physically linking two or more SMPs
- One SMP can directly access memory of another SMP
- Not all processors have equal access time to all memories
- Memory access across link is slower
- If cache coherency is maintained, then may also be called CC-NUMA -
Cache Coherent NUMA
|
Shared Memory (UMA)
Shared Memory (NUMA) |
 Advantages:
Advantages:
- Global address space provides a user-friendly programming perspective
to memory
- Data sharing between tasks is both fast and uniform due to the proximity
of memory to CPUs
 Disadvantages:
Disadvantages:
- Primary disadvantage is the lack of scalability between memory and CPUs.
Adding more CPUs can geometrically increases traffic on the shared
memory-CPU path, and for cache coherent systems, geometrically increase
traffic associated with cache/memory management.
- Programmer responsibility for synchronization constructs that ensure
"correct" access of global memory.
- Expense: it becomes increasingly difficult and expensive to design and
produce shared memory machines with ever increasing numbers of
processors.
|
Parallel Computer Memory Architectures |
Distributed Memory
 General Characteristics:
General Characteristics:
- Like shared memory systems, distributed memory systems vary widely but
share a common characteristic. Distributed memory systems require a
communication network to connect inter-processor memory.
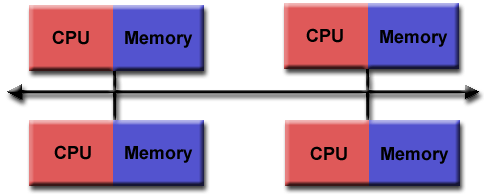
- Processors have their own local memory. Memory addresses in one
processor do not map to another processor, so there is no concept of
global address space across all processors.
- Because each processor has its own local memory, it operates
independently. Changes it makes to its local memory have no effect
on the memory of other processors. Hence, the concept of cache
coherency does not apply.
- When a processor needs access to data in another processor, it is
usually the task of the programmer to explicitly define how and when
data is communicated. Synchronization between tasks is likewise the
programmer's responsibility.
- The network "fabric" used for data transfer varies widely, though it can
can be as simple as Ethernet.
 Advantages:
Advantages:
- Memory is scalable with the number of processors. Increase the number of
processors and the size of memory increases proportionately.
- Each processor can rapidly access its own memory without interference
and without the overhead incurred with trying to maintain cache
coherency.
- Cost effectiveness: can use commodity, off-the-shelf processors and
networking.
 Disadvantages:
Disadvantages:
- The programmer is responsible for many of the details associated with
data communication between processors.
- It may be difficult to map existing data structures, based on global
memory, to this memory organization.
- Non-uniform memory access (NUMA) times
|
Parallel Computer Memory Architectures |
Hybrid Distributed-Shared Memory
- The largest and fastest computers in the world today employ both shared
and distributed memory architectures.
- The shared memory component can be a cache coherent SMP machine and/or
graphics processing units (GPU).
- The distributed memory component is the networking of multiple SMP/GPU
machines, which know only about their own memory - not the memory on another
machine. Therefore, network communications are required to move data from one
SMP/GPU to another.
- Current trends seem to indicate that this type of memory architecture
will continue to prevail and increase at the high end of computing for
the foreseeable future.
- Advantages and Disadvantages: whatever is common to both shared and
distributed memory architectures.
|
Parallel Programming Models |
Overview
- There are several parallel programming models in common use:
- Shared Memory (without threads)
- Threads
- Distributed Memory / Message Passing
- Data Parallel
- Hybrid
- Single Program Multiple Data (SPMD)
- Multiple Program Multiple Data (MPMD)
- Parallel programming models exist as an abstraction above hardware
and memory architectures.
- Although it might not seem apparent, these models are NOT specific
to a particular type of machine or memory architecture. In fact, any
of these models can (theoretically) be implemented on any underlying
hardware. Two examples from the past are discussed below.
- SHARED memory model on a DISTRIBUTED memory machine:
Kendall Square Research (KSR) ALLCACHE approach.
Machine memory was physically distributed across networked machines, but
appeared to the user as a single shared memory (global address space).
Generically, this approach is referred to as "virtual shared memory".
|
 |
- DISTRIBUTED memory model on a SHARED memory machine:
Message Passing Interface (MPI) on SGI Origin 2000.
The SGI Origin 2000 employed the CC-NUMA type of shared memory architecture,
where every task has direct access to global address space spread across all
machines. However, the ability to send and receive messages using MPI, as
is commonly done over a network of distributed memory machines, was
implemented and commonly used.
|
 |
- Which model to use?
This is often a combination of what is available and personal
choice. There is no "best" model, although there certainly are better
implementations of some models over others.
- The following sections describe each of the models mentioned above, and
also discuss some of their actual implementations.
|
Parallel Programming Models |
Shared Memory Model (without threads)
- In this programming model, tasks share a common address space,
which they read and write to asynchronously.
- Various mechanisms such as locks / semaphores may be used to control
access to the shared memory.
- An advantage of this model from the programmer's point of view is that the
notion of data "ownership" is lacking, so there is no need to specify
explicitly the communication of data between tasks. Program
development can often be simplified.
- An important disadvantage in terms of performance is that it becomes
more difficult to understand and manage data locality.
- Keeping data local to the processor that works on it conserves memory
accesses, cache refreshes and bus traffic that occurs when multiple
processors use the same data.
- Unfortunately, controlling data locality is hard to understand and
beyond the control of the average user.
 Implementations:
Implementations:
- Native compilers and/or hardware translate
user program variables into actual memory addresses, which are global.
On stand-alone SMP machines, this is straightforward.
- On distributed shared memory machines, such as the SGI Origin, memory
is physically distributed across a network of machines, but made
global through specialized hardware and software.
|
Parallel Programming Models |
Threads Model
- This programming model is a type of shared memory programming.
- In the threads model of parallel programming, a single process can have
multiple, concurrent execution paths.
- Perhaps the most simple analogy that can be used to describe threads is the
concept of a single program that includes a number of subroutines:
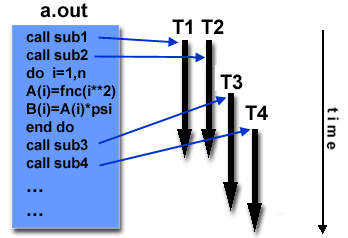
- The main program a.out is scheduled to run by the
native operating system. a.out loads and acquires all of the
necessary system and user resources to run.
- a.out performs some serial work, and then creates
a number of tasks (threads) that can be scheduled and run by the
operating system concurrently.
- Each thread has local data, but also, shares the entire resources of
a.out. This saves the overhead associated with
replicating a program's resources for each thread. Each thread also
benefits from a global memory view because it shares the memory space
of a.out.
- A thread's work may best be described as a subroutine within
the main program. Any thread can execute any subroutine at the
same time as other threads.
- Threads communicate with each other through global memory (updating
address locations). This requires synchronization constructs to ensure
that more than one thread is not updating the same global address at
any time.
- Threads can come and go, but a.out remains present
to provide the necessary shared resources until the
application has completed.
 Implementations:
Implementations:
 More Information:
More Information:
|
Parallel Programming Models |
Distributed Memory / Message Passing Model
- This model demonstrates the following characteristics:
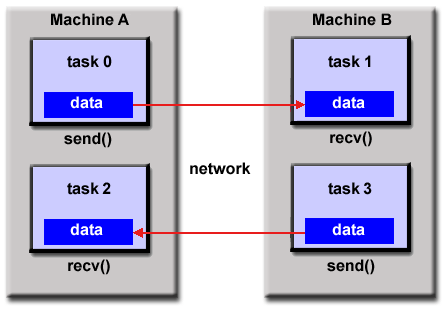
- A set of tasks that use their own local memory during computation.
Multiple tasks can reside on the same physical machine and/or
across an arbitrary number of machines.
- Tasks exchange data through communications by sending and
receiving messages.
- Data transfer usually requires cooperative operations to be performed
by each process. For example, a send operation must have a matching
receive operation.
 Implementations:
Implementations:
- From a programming perspective, message passing implementations usually
comprise a library of subroutines. Calls to these subroutines
are imbedded in source code. The programmer is responsible for determining
all parallelism.
- Historically, a variety of message passing libraries have been
available since the 1980s. These implementations differed substantially
from each other making it difficult for programmers to develop portable
applications.
- In 1992, the MPI Forum was formed with the primary goal of establishing
a standard interface for message passing implementations.
- Part 1 of the Message Passing Interface (MPI) was released in
1994. Part 2 (MPI-2) was released in 1996.
Both MPI specifications are available on the web at
http://www-unix.mcs.anl.gov/mpi/.
- MPI is now the "de facto" industry
standard for message passing, replacing virtually all other
message passing implementations used for production work.
MPI implementations exist for virtually all popular parallel computing
platforms. Not all implementations include everything in both MPI1
and MPI2.
 More Information:
More Information:
|
Parallel Programming Models |
Data Parallel Model
- The data parallel model demonstrates the following characteristics:
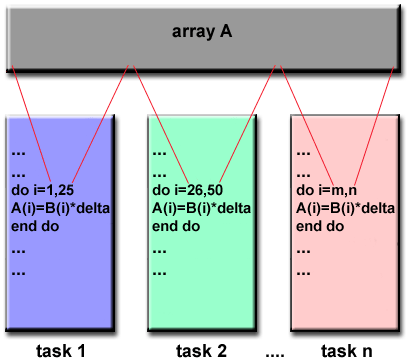
- Most of the parallel work focuses on performing operations on a
data set. The data set is typically organized into a common
structure, such as an array or cube.
- A set of tasks work collectively on the same data structure, however,
each task works on a different partition of the same data structure.
- Tasks perform the same operation on their partition of work, for
example, "add 4 to every array element".
- On shared memory architectures, all tasks may have access to the data
structure through global memory. On distributed memory architectures
the data structure is split up and resides as "chunks" in the local
memory of each task.
 Implementations:
Implementations:
- Programming with the data parallel model is usually accomplished by
writing a program with data parallel constructs. The constructs can be
calls to a data parallel subroutine library or, compiler directives
recognized by a data parallel compiler.
- Fortran 90 and 95 (F90, F95): ISO/ANSI standard extensions to
Fortran 77.
- Contains everything that is in Fortran 77
- New source code format; additions to character set
- Additions to program structure and commands
- Variable additions - methods and arguments
- Pointers and dynamic memory allocation added
- Array processing (arrays treated as objects) added
- Recursive and new intrinsic functions added
- Many other new features
Implementations are available for most common parallel platforms.
- High Performance Fortran (HPF): Extensions to Fortran 90 to
support data parallel programming.
- Contains everything in Fortran 90
- Directives to tell compiler how to distribute data added
- Assertions that can improve optimization of generated code added
- Data parallel constructs added (now part of Fortran 95)
HPF compilers were relatively common in the 1990s, but are no longer
commonly implemented.
- Compiler Directives: Allow the programmer to specify the
distribution and alignment of data. Fortran implementations are
available for most common parallel platforms.
- Distributed memory implementations of this model usually require
the compiler to produce object code with calls to a message
passing library (MPI) for data distribution. All message passing is
done invisibly to the programmer.
|
Parallel Programming Models |
Hybrid Model
- A hybrid model combines more than one of the previously described
programming models.
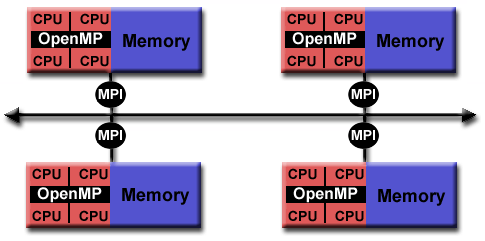
- Currently, a common example of a hybrid model is the combination
of the message passing model (MPI) with the threads model (OpenMP).
- Threads perform computationally intensive kernels using local,
on-node data
- Communications between processes on different nodes occurs
over the network using MPI
- This hybrid model lends itself well to the increasingly common hardware
environment of clustered multi/many-core machines.
- Another similar and increasingly popular example of a hybrid model is
using MPI with GPU (Graphics Processing Unit) programming.
- GPUs perform computationally intensive kernels using local,
on-node data
- Communications between processes on different nodes occurs
over the network using MPI
|
Parallel Programming Models |
SPMD and MPMD
 Single Program Multiple Data (SPMD):
Single Program Multiple Data (SPMD):
- SPMD is actually a "high level" programming model that can be
built upon any combination of the previously mentioned parallel
programming models.
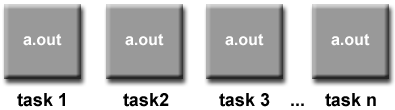
- SINGLE PROGRAM: All tasks execute their copy of the same program
simultaneously. This program can be threads, message passing,
data parallel or hybrid.
- MULTIPLE DATA: All tasks may use different data
- SPMD programs usually have the necessary logic programmed into them to
allow different tasks to branch or conditionally execute only those
parts of the program they are designed to execute. That is, tasks
do not necessarily have to execute the entire program - perhaps only a
portion of it.
- The SPMD model, using message passing or hybrid programming,
is probably the most commonly used parallel programming model
for multi-node clusters.
 Multiple Program Multiple Data (MPMD):
Multiple Program Multiple Data (MPMD):
- Like SPMD, MPMD is actually a "high level" programming model that can
be built upon any combination of the previously mentioned parallel
programming models.

- MULTIPLE PROGRAM: Tasks may execute different programs
simultaneously. The programs can be threads, message passing,
data parallel or hybrid.
- MULTIPLE DATA: All tasks may use different data
- MPMD applications are not as common as SPMD applications, but may
be better suited for certain types of problems, particularly those
that lend themselves better to functional decomposition
than domain decomposition (discussed later under
Partioning).
|
Designing Parallel Programs |
Automatic vs. Manual Parallelization
- Designing and developing parallel programs has characteristically been a
very manual process. The programmer is typically responsible for
both identifying and actually implementing parallelism.
- Very often, manually developing parallel codes is a time consuming,
complex, error-prone and iterative process.
- For a number of years now, various tools have been available to assist
the programmer with converting serial programs into parallel programs.
The most common type of tool used to automatically parallelize a serial
program is a parallelizing compiler or pre-processor.
- A parallelizing compiler generally works in two different ways:
- Fully Automatic
- The compiler analyzes the source code and
identifies opportunities for parallelism.
- The analysis includes
identifying inhibitors to parallelism and possibly a cost
weighting on whether or not the parallelism would actually
improve performance.
- Loops (do, for) loops are the most frequent target for
automatic parallelization.
- Programmer Directed
- Using "compiler directives" or possibly compiler flags,
the programmer explicitly tells the compiler how to
parallelize the code.
- May be able to be used in conjunction with some degree of
automatic parallelization also.
- If you are beginning with an existing serial code and have time
or budget constraints, then automatic parallelization may be
the answer. However, there are several important caveats that
apply to automatic parallelization:
- Wrong results may be produced
- Performance may actually degrade
- Much less flexible than manual parallelization
- Limited to a subset (mostly loops) of code
- May actually not parallelize code if the analysis suggests there
are inhibitors or the code is too complex
- The remainder of this section applies to the manual method of
developing parallel codes.
|
Designing Parallel Programs |
Understand the Problem and the Program
- Undoubtedly, the first step in developing parallel software is to
first understand the problem that you wish to solve in parallel.
If you are starting with a serial program, this necessitates
understanding the existing code also.
- Before spending time in an attempt to develop a parallel solution
for a problem, determine whether or not the problem is one that can
actually be parallelized.
- Example of Parallelizable Problem:
|
Calculate the potential energy for each of several thousand
independent conformations of a molecule.
When done, find the minimum energy conformation.
|
This problem is able to be solved in parallel. Each of the
molecular conformations is independently determinable.
The calculation of the minimum energy conformation is also a
parallelizable problem.
- Example of a Non-parallelizable Problem:
Calculation of the Fibonacci series (0,1,1,2,3,5,8,13,21,...) by use of
the formula:
F(n) = F(n-1) + F(n-2)
|
This is a non-parallelizable problem because the calculation of the
Fibonacci sequence as shown would entail
dependent calculations rather than independent ones.
The calculation of the F(n) value uses those of
both F(n-1) and F(n-2). These three terms cannot be calculated
independently and therefore, not in parallel.
- Identify the program's hotspots:
- Know where most of the real work is being done.
The majority of scientific and technical programs usually
accomplish most of their work in a few places.
- Profilers and performance analysis tools can help here
- Focus on parallelizing the hotspots and ignore those sections
of the program that account for little CPU usage.
- Identify bottlenecks in the program
- Are there areas that are disproportionately slow, or cause
parallelizable work to halt or be deferred?
For example, I/O is usually something that slows a program down.
- May be possible to restructure the program or use a different
algorithm to reduce or eliminate unnecessary slow areas
- Identify inhibitors to parallelism. One common class of inhibitor
is data dependence, as demonstrated by the Fibonacci sequence
above.
- Investigate other algorithms if possible. This may be the single most
important consideration when designing a parallel application.
|
 |
|
Designing Parallel Programs |
Partitioning
- One of the first steps in designing a parallel program is to break the
problem into discrete "chunks" of work that can be distributed to
multiple tasks. This is known as decomposition or partitioning.
- There are two basic ways to partition computational work among parallel
tasks: domain decomposition and
functional decomposition.
 Domain Decomposition:
Domain Decomposition:
- In this type of partitioning, the data associated with a problem
is decomposed. Each parallel task then works on a portion of
of the data.
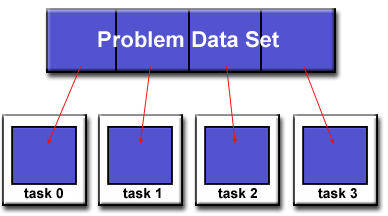
- There are different ways to partition data:
 Functional Decomposition:
Functional Decomposition:
- In this approach, the focus is on the computation that is to be
performed rather than on the data manipulated by the computation.
The problem is decomposed according to the work that must be done.
Each task then performs a portion of the overall work.
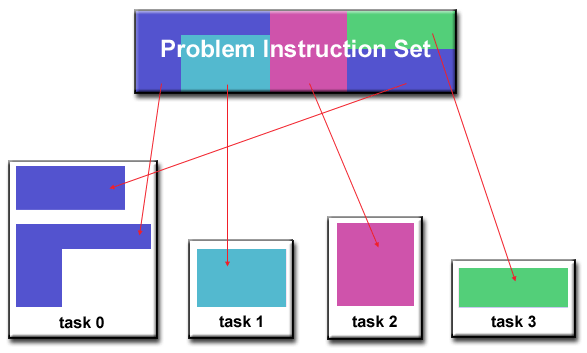
- Functional decomposition lends itself well to problems that can be
split into different tasks. For example:
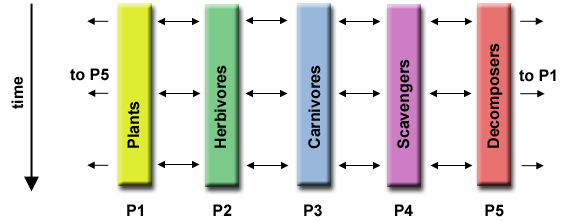
- Ecosystem Modeling
Each program calculates the population
of a given group, where each group's growth depends on that of its
neighbors. As time progresses, each process calculates
its current state, then exchanges information with the neighbor
populations. All tasks then progress to calculate the state at the
next time step.
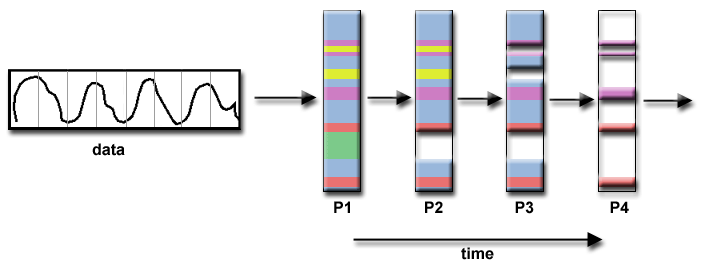
- Signal Processing
An audio signal data set is passed
through four distinct computational filters. Each filter is a
separate process. The first segment of data must pass through the
first filter before progressing to the second. When it does, the
second segment of data passes through the first filter. By the time
the fourth segment of data is in the first filter, all four
tasks are busy.
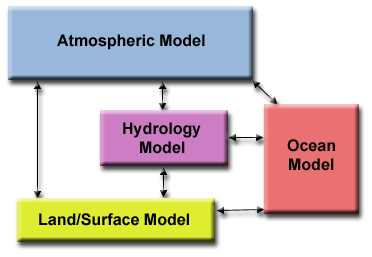
- Climate Modeling
Each model component can be thought of as a separate task.
Arrows represent exchanges of data between components during
computation: the atmosphere model generates wind velocity data
that are used by the ocean model, the ocean model generates sea
surface temperature data that are used by the atmosphere model,
and so on.
- Combining these two types of problem decomposition is common and natural.
|
Designing Parallel Programs |
Communications
 Who Needs Communications?
Who Needs Communications?
 Factors to Consider:
Factors to Consider:
There are a number of important factors to consider when designing your
program's inter-task communications:
- Cost of communications
- Inter-task communication virtually always implies overhead.
- Machine cycles and resources that could be used for computation
are instead used to package and transmit data.
- Communications frequently require some type of synchronization
between tasks, which can result in tasks spending time "waiting"
instead of doing work.
- Competing communication traffic can saturate the available network
bandwidth, further aggravating performance problems.
- Latency vs. Bandwidth
- latency is the time it takes to send a minimal (0 byte)
message from point A to point B. Commonly expressed as microseconds.
- bandwidth is the amount of data that can be communicated
per unit of time. Commonly expressed as megabytes/sec or gigabytes/sec.
- Sending many small messages can cause latency to dominate communication
overheads. Often it is more efficient to package small messages into a
larger message, thus increasing the effective communications bandwidth.
- Visibility of communications
- With the Message Passing Model, communications are explicit and
generally quite visible and under the control of the programmer.
- With the Data Parallel Model, communications often occur
transparently to the programmer, particularly on distributed
memory architectures. The programmer may not even be able to
know exactly how inter-task communications are being accomplished.
- Synchronous vs. asynchronous communications
- Synchronous communications require some type of "handshaking"
between tasks that are sharing data. This can be explicitly
structured in code by the programmer, or it may happen at a
lower level unknown to the programmer.
- Synchronous communications are often referred to as
blocking communications since other work must
wait until the communications have completed.
- Asynchronous communications allow tasks to transfer data independently
from one another. For example, task 1 can prepare and send a
message to task 2, and then immediately begin doing other work.
When task 2 actually receives the data doesn't matter.
- Asynchronous communications are often referred to as
non-blocking communications since other work can
be done while the communications are taking place.
- Interleaving computation with communication is the single greatest
benefit for using asynchronous communications.
- Scope of communications
- Knowing which tasks must communicate with each other is critical during
the design stage of a parallel code. Both of the two scopings
described below can be implemented synchronously or asynchronously.
- Point-to-point - involves two tasks with one task
acting as the sender/producer of data, and the other acting as
the receiver/consumer.
- Collective - involves data sharing between more than
two tasks, which are often specified as being members in a common
group, or collective. Some common variations (there are more):
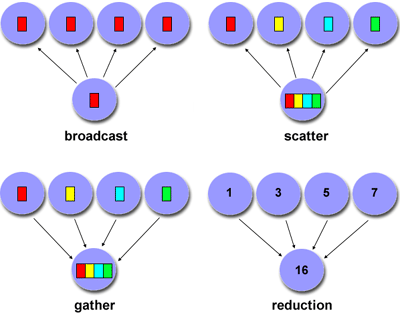
- Efficiency of communications
- Very often, the programmer will have a choice with regard to
factors that can affect communications performance. Only a
few are mentioned here.
- Which implementation for a given model should be used? Using
the Message Passing Model as an
example, one MPI implementation may be faster on a given
hardware platform than another.
- What type of communication operations should be used? As
mentioned previously, asynchronous communication operations
can improve overall program performance.
- Network media - some platforms may offer more than one network
for communications. Which one is best?
- Overhead and Complexity
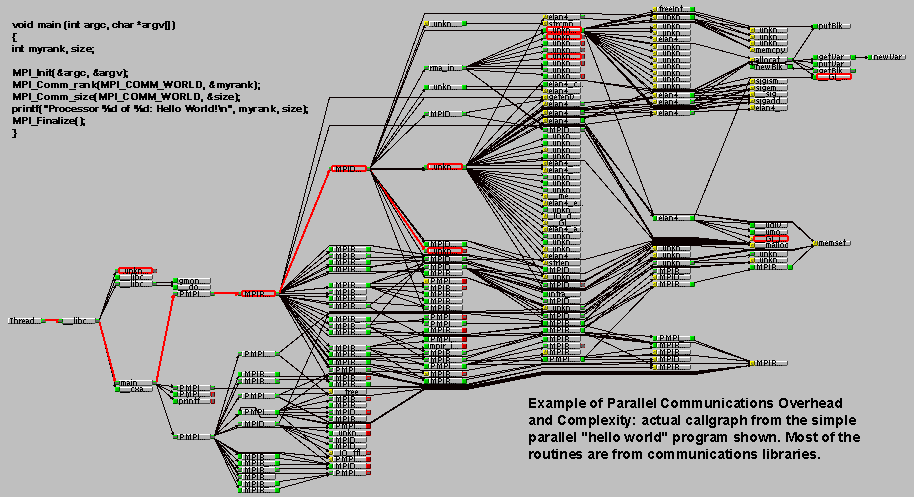
- Finally, realize that this is only a partial list of things to consider!!!
|
Designing Parallel Programs |
Synchronization
 Types of Synchronization:
Types of Synchronization:
- Barrier
- Usually implies that all tasks are involved
- Each task performs its work until it reaches the barrier. It then
stops, or "blocks".
- When the last task reaches the barrier, all tasks are synchronized.
- What happens from here varies. Often, a serial section of work must
be done. In other cases, the tasks are automatically released to
continue their work.
- Lock / semaphore
- Can involve any number of tasks
- Typically used to serialize (protect) access to global data
or a section of code. Only one task at a time may use (own) the
lock / semaphore / flag.
- The first task to acquire the lock "sets" it. This task can then
safely (serially) access the protected data or code.
- Other tasks can attempt to acquire the lock but must wait until the
task that owns the lock releases it.
- Can be blocking or non-blocking
- Synchronous communication operations
- Involves only those tasks executing a communication operation
- When a task performs a communication operation, some form of
coordination is required with the other task(s) participating in
the communication. For example, before a task can perform a
send operation, it must first receive an acknowledgment from the
receiving task that it is OK to send.
- Discussed previously in the Communications section.
|
Designing Parallel Programs |
Data Dependencies
 Definition:
Definition:
- A dependence exists between program statements when
the order of statement execution affects the results of the program.
- A data dependence results from multiple use of the same
location(s) in storage by different tasks.
- Dependencies are important to parallel programming because they are one
of the primary inhibitors to parallelism.
 Examples:
Examples:
- Loop carried data dependence
DO 500 J = MYSTART,MYEND
A(J) = A(J-1) * 2.0
500 CONTINUE
|
The value of A(J-1) must be computed before the value of A(J),
therefore A(J) exhibits a data dependency on A(J-1).
Parallelism is inhibited.
If Task 2 has A(J) and task 1 has A(J-1),
computing the correct value of A(J) necessitates:
- Distributed memory architecture - task 2 must obtain the value
of A(J-1) from task 1 after task 1 finishes its computation
- Shared memory architecture - task 2 must read A(J-1) after
task 1 updates it
- Loop independent data dependence
task 1 task 2
------ ------
X = 2 X = 4
. .
. .
Y = X**2 Y = X**3
|
As with the previous example, parallelism is inhibited.
The value of Y is dependent on:
- Distributed memory architecture - if or when the value of X is
communicated between the tasks.
- Shared memory architecture - which task last stores the value of X.
- Although all data dependencies are important to identify when designing
parallel programs, loop carried dependencies are particularly important
since loops are possibly the most common target of parallelization efforts.
 How to Handle Data Dependencies:
How to Handle Data Dependencies:
- Distributed memory architectures - communicate required data at
synchronization points.
- Shared memory architectures -synchronize read/write operations between
tasks.
|
Designing Parallel Programs |
Load Balancing
- Load balancing refers to the practice of distributing work among tasks
so that all tasks are kept busy all of the time.
It can be considered a minimization of task idle time.
- Load balancing is important to parallel programs for performance
reasons. For example, if all tasks are subject to a barrier
synchronization point, the slowest task will determine the overall
performance.
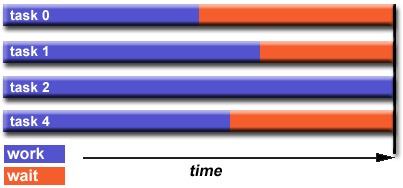
 How to Achieve Load Balance:
How to Achieve Load Balance:
- Equally partition the work each task receives
- For array/matrix operations where each task performs similar
work, evenly distribute the data set among the tasks.
- For loop iterations where the work done in each iteration
is similar, evenly distribute the iterations across the tasks.
- If a heterogeneous mix of machines with varying performance
characteristics are being used, be sure to use some type of performance
analysis tool to detect any load imbalances. Adjust work accordingly.
- Use dynamic work assignment
- Certain classes of problems result in load imbalances even if data
is evenly distributed among tasks:
- Sparse arrays - some tasks will have actual data to work on
while others have mostly "zeros".
- Adaptive grid methods - some tasks may need to refine their
mesh while others don't.
- N-body simulations - where some particles may migrate
to/from their original task domain to another task's; where
the particles owned by some tasks require more work than
those owned by other tasks.
- When the amount of work each task will perform is intentionally
variable, or is unable to be predicted, it may be helpful to use
a scheduler - task pool approach. As each task finishes
its work, it queues to get a new piece of work.
- It may become necessary to design an algorithm which detects and handles
load imbalances as they occur dynamically within the code.
|
Designing Parallel Programs |
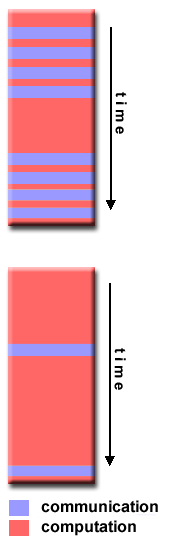
Granularity
 Computation / Communication Ratio:
Computation / Communication Ratio:
- In parallel computing, granularity is a qualitative measure of the ratio
of computation to communication.
- Periods of computation are typically separated from periods of
communication by synchronization events.
 Fine-grain Parallelism:
Fine-grain Parallelism:
- Relatively small amounts of computational work are done between
communication events
- Low computation to communication ratio
- Facilitates load balancing
- Implies high communication overhead and less opportunity for
performance enhancement
- If granularity is too fine it is possible that the overhead
required for communications and synchronization between tasks
takes longer than the computation.
 Coarse-grain Parallelism:
Coarse-grain Parallelism:
- Relatively large amounts of computational work are done between
communication/synchronization events
- High computation to communication ratio
- Implies more opportunity for performance increase
- Harder to load balance efficiently
 Which is Best?
Which is Best?
- The most efficient granularity is dependent on the algorithm and the
hardware environment in which it runs.
- In most cases the overhead associated with communications and
synchronization is high relative to execution speed
so it is advantageous to have coarse granularity.
- Fine-grain parallelism can help reduce overheads due to load imbalance.
|
|
|
Designing Parallel Programs |
I/O
 The Bad News:
The Bad News:
- I/O operations are generally regarded as inhibitors to parallelism
- Parallel I/O systems may be immature or not available for all platforms
- In an environment where all tasks see the same file space, write
operations can result in file overwriting
- Read operations can be affected by the file server's ability to handle
multiple read requests at the same time
- I/O that must be conducted over the network (NFS, non-local) can cause
severe bottlenecks and even crash file servers.
 The Good News:
The Good News:
- Parallel file systems are available. For example:
- GPFS: General Parallel File System for AIX (IBM)
- Lustre: for Linux clusters (Oracle)
- PVFS/PVFS2: Parallel Virtual File System for Linux clusters
(Clemson/Argonne/Ohio State/others)
- PanFS: Panasas ActiveScale File System for Linux clusters (Panasas,
Inc.)
- HP SFS: HP StorageWorks Scalable File Share. Lustre based parallel file
system (Global File System for Linux) product from HP
- The parallel I/O programming interface specification for MPI has been
available since 1996 as part of MPI-2. Vendor and "free" implementations
are now commonly available.
- A few pointers:
- Rule #1: Reduce overall I/O as much as possible
- If you have access to a parallel file system, investigate using
it.
- Writing large chunks of data rather than small packets is usually
significantly more efficient.
- Confine I/O to specific serial portions of the job, and then use
parallel communications to distribute data to parallel tasks.
For example, Task 1 could read an input file and then communicate
required data to other tasks. Likewise, Task 1 could perform
write operation after receiving required data from all other tasks.
- Use local, on-node file space for I/O if possible.
For example, each node may have /tmp filespace which can used.
This is usually much more efficient than performing I/O over the
network to one's home directory.
|
Designing Parallel Programs |
Limits and Costs of Parallel Programming
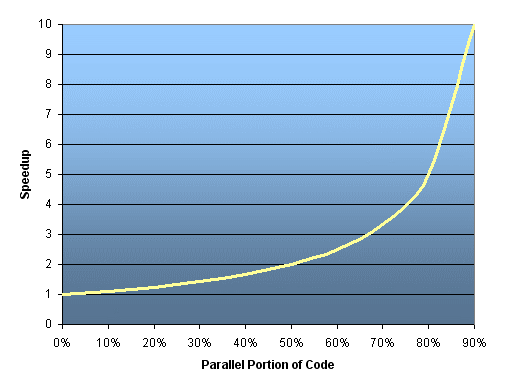
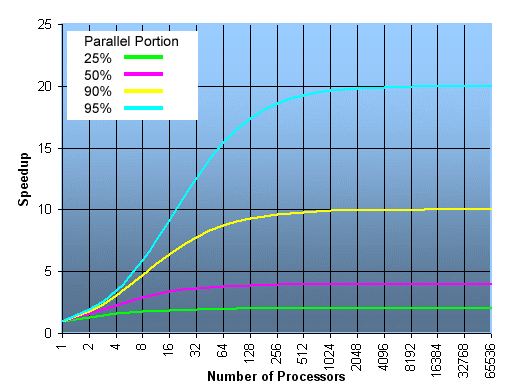
 Amdahl's Law:
Amdahl's Law:
 Complexity:
Complexity:
- In general, parallel applications are much more complex than corresponding
serial applications, perhaps an order of magnitude. Not only do you have
multiple instruction streams executing at the same time, but you also have
data flowing between them.
- The costs of complexity are measured in programmer time in virtually every
aspect of the software development cycle:
- Design
- Coding
- Debugging
- Tuning
- Maintenance
- Adhering to "good" software development practices is essential when
when working with parallel applications - especially if somebody besides
you will have to work with the software.
 Portability:
Portability:
- Thanks to standardization in several APIs, such as MPI, POSIX threads,
HPF and OpenMP, portability issues with parallel programs are not as
serious as in years past. However...
- All of the usual portability issues associated with serial programs
apply to parallel programs. For example, if you use vendor "enhancements"
to Fortran, C or C++, portability will be a problem.
- Even though standards exist for several APIs, implementations will differ
in a number of details, sometimes to the point of requiring code
modifications in order to effect portability.
- Operating systems can play a key role in code portability issues.
- Hardware architectures are characteristically highly variable and can
affect portability.
 Resource Requirements:
Resource Requirements:
- The primary intent of parallel programming is to decrease execution
wall clock time, however in order to accomplish this, more CPU time
is required. For example, a parallel code that runs in 1 hour on 8
processors actually uses 8 hours of CPU time.
- The amount of memory required can be greater for parallel codes than
serial codes, due to the need to replicate data and for overheads
associated with parallel support libraries and subsystems.
- For short running parallel programs, there can actually be a decrease
in performance compared to a similar serial implementation. The overhead
costs associated with setting up the parallel environment, task creation,
communications and task termination can comprise a significant portion of
the total execution time for short runs.
 Scalability:
Scalability:
- The ability of a parallel program's performance to scale is a result
of a number of interrelated factors. Simply adding more machines
is rarely the answer.
- The algorithm may have inherent limits to scalability. At some point,
adding more resources causes performance to decrease. Most parallel
solutions demonstrate this characteristic at some point.
- Hardware factors play a significant role in scalability. Examples:
- Memory-cpu bus bandwidth on an SMP machine
- Communications network bandwidth
- Amount of memory available on any given machine or set of machines
- Processor clock speed
- Parallel support libraries and subsystems software can limit scalability
independent of your application.
|
Designing Parallel Programs |
Performance Analysis and Tuning
- As with debugging, monitoring and analyzing parallel program execution
is significantly more of a challenge than for serial programs.
- A number of parallel tools for execution monitoring and program analysis
are available.
- Some are quite useful; some are cross-platform also.
- Some starting points:
- Work remains to be done, particularly in the area of scalability.
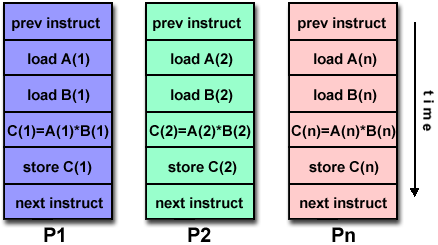
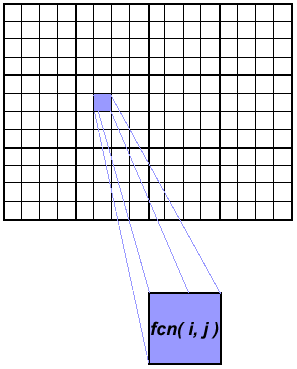
Array Processing
- This example demonstrates calculations on 2-dimensional array
elements, with the computation on each array element being
independent from other array elements.
- The serial program calculates one element at a time in sequential
order.
- Serial code could be of the form:
do j = 1,n
do i = 1,n
a(i,j) = fcn(i,j)
end do
end do
|
- The calculation of elements is independent of one another -
leads to an embarrassingly parallel situation.
- The problem should be computationally intensive.
|
|
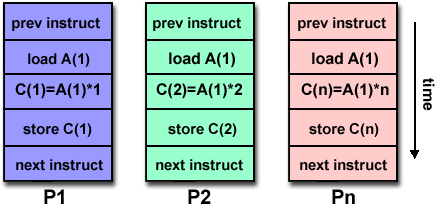
Array Processing
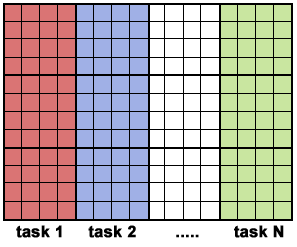
Parallel Solution 1
- Arrays elements are distributed so that each processor owns a
portion of an array (subarray).
- Independent calculation of array elements ensures there is no
need for communication between tasks.
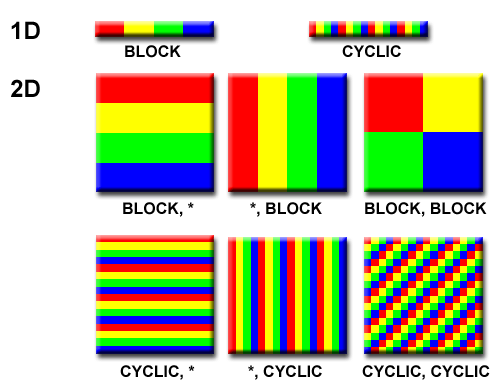
- Distribution scheme is chosen by other criteria, e.g. unit stride
(stride of 1) through the subarrays. Unit stride maximizes
cache/memory usage.
- Since it is desirable to have unit stride through the subarrays, the
choice of a distribution scheme depends on the programming language.
See the Block - Cyclic Distributions Diagram
for the options.
- After the array is distributed, each task
executes the portion of the loop corresponding to the data it owns.
For example, with Fortran block distribution:
do j = mystart, myend
do i = 1,n
a(i,j) = fcn(i,j)
end do
end do
|
- Notice that only the outer loop variables are different from the serial
solution.
|
|
 One Possible Solution:
One Possible Solution:
- Implement as a Single Program Multiple Data (SPMD) model.
- Master process initializes array, sends info to worker
processes and receives results.
- Worker process receives info, performs its share of
computation and sends results to master.
- Using the Fortran storage scheme, perform block
distribution of the array.
- Pseudo code solution:
red highlights changes for
parallelism.
find out if I am MASTER or WORKER
if I am MASTER
initialize the array
send each WORKER info on part of array it owns
send each WORKER its portion of initial array
receive from each WORKER results
else if I am WORKER
receive from MASTER info on part of array I own
receive from MASTER my portion of initial array
# calculate my portion of array
do j = my first column,my last column
do i = 1,n
a(i,j) = fcn(i,j)
end do
end do
send MASTER results
endif
|
- Example MPI Program in C:
mpi_array.c
- Example MPI Program in Fortran:
mpi_array.f
Array Processing
Parallel Solution 2: Pool of Tasks
- The previous array solution demonstrated static load balancing:
- Each task has a fixed amount of work to do
- May be significant idle time for faster or more lightly loaded
processors - slowest tasks determines overall performance.
- Static load balancing is not usually a major concern if all tasks
are performing the same amount of work on identical machines.
- If you have a load balance problem (some tasks work faster than
others), you may benefit by using a "pool of tasks"
scheme.
 Pool of Tasks Scheme:
Pool of Tasks Scheme:
 Discussion:
Discussion:
- In the above pool of tasks example, each task calculated an individual
array element as a job. The computation to communication ratio is
finely granular.
- Finely granular solutions incur more communication overhead in order
to reduce task idle time.
- A more optimal solution might be to distribute more work with each job.
The "right" amount of work is problem dependent.
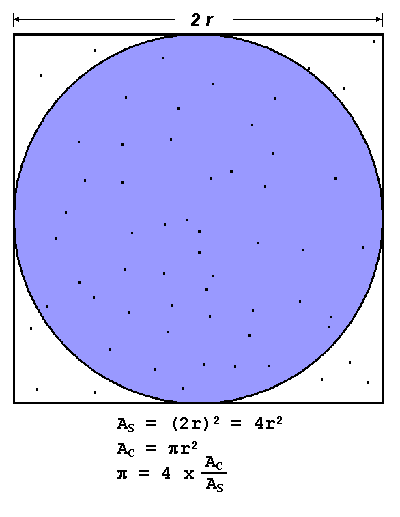
PI Calculation
- The value of PI can be calculated in a number of ways. Consider the
following method of approximating PI
- Inscribe a circle in a square
- Randomly generate points in the square
- Determine the number of points in the square that are also in the circle
- Let r be the number of points in the circle divided by the number of
points in the square
- PI ~ 4 r
- Note that the more points generated, the better the approximation
- Serial pseudo code for this procedure:
npoints = 10000
circle_count = 0
do j = 1,npoints
generate 2 random numbers between 0 and 1
xcoordinate = random1
ycoordinate = random2
if (xcoordinate, ycoordinate) inside circle
then circle_count = circle_count + 1
end do
PI = 4.0*circle_count/npoints
|
- Note that most of the time in running this program would be
spent executing the loop
- Leads to an embarrassingly parallel solution
- Computationally intensive
- Minimal communication
- Minimal I/O
|
|
PI Calculation
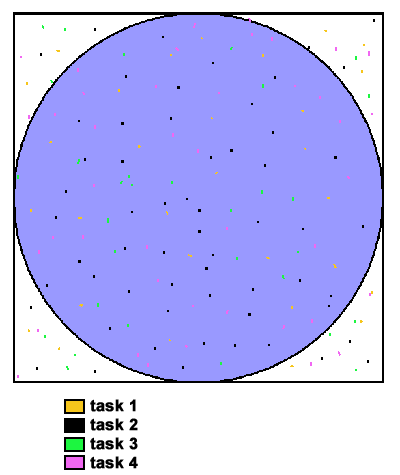
Parallel Solution
- Parallel strategy: break the loop into portions that can be
executed by the tasks.
- For the task of approximating PI:
- Each task executes its portion of the loop a number of times.
- Each task can do its work without requiring any information
from the other tasks (there are no data dependencies).
- Uses the SPMD model. One task acts as master and collects
the results.
- Pseudo code solution:
red highlights changes for
parallelism.
npoints = 10000
circle_count = 0
p = number of tasks
num = npoints/p
find out if I am MASTER or WORKER
do j = 1,num
generate 2 random numbers between 0 and 1
xcoordinate = random1
ycoordinate = random2
if (xcoordinate, ycoordinate) inside circle
then circle_count = circle_count + 1
end do
if I am MASTER
receive from WORKERS their circle_counts
compute PI (use MASTER and WORKER calculations)
else if I am WORKER
send to MASTER circle_count
endif
|
|
|
Simple Heat Equation
- Most problems in parallel computing require communication among
the tasks.
A number of common problems require communication with "neighbor"
tasks.
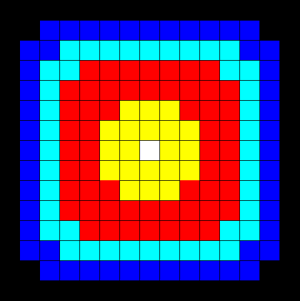
- The heat equation describes the temperature change over time,
given initial temperature distribution and boundary conditions.
- A finite differencing scheme is employed to solve the
heat equation numerically on a square region.
- The initial temperature is zero on the boundaries and high in the middle.
- The boundary temperature is held at zero.
- For the fully explicit problem, a time stepping algorithm is used.
The elements of a 2-dimensional array represent the temperature at
points on the square.
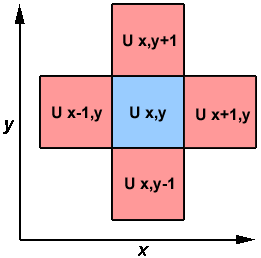
- The calculation of an element is dependent upon neighbor element
values.
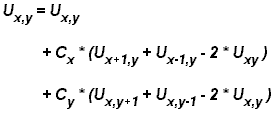
- A serial program would contain code like:
do iy = 2, ny - 1
do ix = 2, nx - 1
u2(ix, iy) =
u1(ix, iy) +
cx * (u1(ix+1,iy) + u1(ix-1,iy) - 2.*u1(ix,iy)) +
cy * (u1(ix,iy+1) + u1(ix,iy-1) - 2.*u1(ix,iy))
end do
end do
|
| 
|
Simple Heat Equation
Parallel Solution
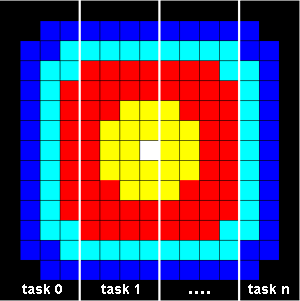
- Implement as an SPMD model
- The entire array is partitioned and distributed as subarrays to all
tasks. Each task owns a portion of the total array.
- Determine data dependencies
- Master process sends initial info to workers, and then waits
to collect results from all workers
- Worker process calculates solution within specified number of time steps,
communicating as necessary with neighbor processes
- Pseudo code solution:
red highlights changes for parallelism.
find out if I am MASTER or WORKER
if I am MASTER
initialize array
send each WORKER starting info and subarray
receive results from each WORKER
else if I am WORKER
receive from MASTER starting info and subarray
do t = 1, nsteps
update time
send neighbors my border info
receive from neighbors their border info
update my portion of solution array
end do
send MASTER results
endif
|
- Example MPI Program in C:
mpi_heat2D.c
- Example MPI Program in Fortran:
mpi_heat2D.f
1-D Wave Equation
- In this example, the amplitude along a uniform, vibrating string is
calculated after a specified amount of time has elapsed.
- The calculation involves:
- the amplitude on the y axis
- i as the position index along the x axis
- node points imposed along the string
- update of the amplitude at discrete time steps.
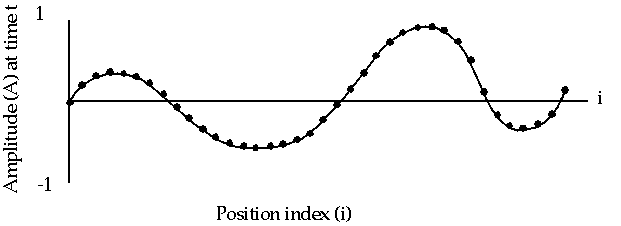
- The equation to be solved is the one-dimensional wave equation:
A(i,t+1) = (2.0 * A(i,t)) - A(i,t-1)
+ (c * (A(i-1,t) - (2.0 * A(i,t)) + A(i+1,t)))
where c is a constant
- Note that amplitude will depend on previous timesteps (t, t-1) and
neighboring points (i-1, i+1). Data dependence will mean that a
parallel solution will involve communications.
1-D Wave Equation
Parallel Solution
- Implement as an SPMD model
- The entire amplitude array is partitioned and distributed as
subarrays to all tasks. Each task owns a portion of
the total array.
- Load balancing: all points require equal work, so the points should
be divided equally
- A block decomposition would have the work partitioned into the number
of tasks as chunks, allowing each task to own mostly contiguous data points.
- Communication need only occur on data borders. The larger the block size
the less the communication.
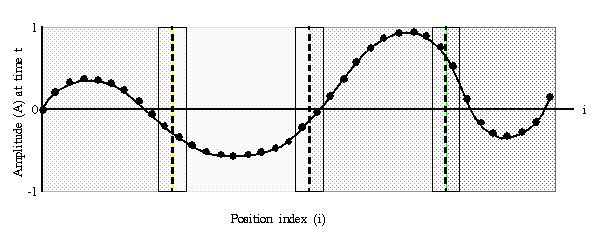
- Pseudo code solution:
find out number of tasks and task identities
#Identify left and right neighbors
left_neighbor = mytaskid - 1
right_neighbor = mytaskid +1
if mytaskid = first then left_neigbor = last
if mytaskid = last then right_neighbor = first
find out if I am MASTER or WORKER
if I am MASTER
initialize array
send each WORKER starting info and subarray
else if I am WORKER`
receive starting info and subarray from MASTER
endif
#Update values for each point along string
#In this example the master participates in calculations
do t = 1, nsteps
send left endpoint to left neighbor
receive left endpoint from right neighbor
send right endpoint to right neighbor
receive right endpoint from left neighbor
#Update points along line
do i = 1, npoints
newval(i) = (2.0 * values(i)) - oldval(i)
+ (sqtau * (values(i-1) - (2.0 * values(i)) + values(i+1)))
end do
end do
#Collect results and write to file
if I am MASTER
receive results from each WORKER
write results to file
else if I am WORKER
send results to MASTER
endif
|
- Example MPI Program in C:
mpi_wave.c
- Example MPI Program in Fortran:
mpi_wave.f
This completes the tutorial.
 |
Please complete the online evaluation form. |
Where would you like to go now?
|
References and More Information |
- Author: Blaise Barney, Livermore
Computing.
- A search on the WWW for "parallel programming" or "parallel computing"
will yield a wide variety of information.
- Recommended reading:
- Photos/Graphics have been
created by the author, created by other LLNL employees,
obtained from non-copyrighted, government or public domain (such as
http://commons.wikimedia.org/) sources,
or used with the permission of authors from other presentations and
web pages.
- History: These materials have evolved from the following
sources, which are no longer maintained or available.
- Tutorials located in the Maui High Performance Computing Center's
"SP Parallel Programming Workshop".
- Tutorials located at the Cornell Theory Center's "Education and
Training" web page.