Data Representation - Integers
Binary Integers: Integers (..., -3, -2, -1, 0, 1, 2, 3, ...) are the simplest type of number that you can use in a program. In mathematics, there are an infinite number of integers. However, a computer can represent only a finite number of integers because it has registers of a fixed size (in number of bits) and only a finite amount of main memory. The computer stores integers (positive, negative, and zero) in binary form. Depending on the computer and the computer language, an integer can occupy two or four bytes of main memory. The amount of storage required by an integer determines the range of integer values that the computer can represent.
For example, an IBM-PC stores an integer in two bytes, that is 16 bits. Since there are 2^16 = 65,536 ways of arranging 16 zeros and ones, such a computer can represent 65,536 integers (positive, negative, and zero) in two bytes. Half the integers in this range are negative (that is, less than zero) and half are nonnegative (that is, greater than or equal to zero). Therefore, on an IBM-PC, a two-byte integer can have a value in the range -32,768 (-2^15) to +32,767 (2^15 - 1).
Similarly, a Sun Workstation stores integers in four bytes and, consequently, can represent 2^32 = 4,294,967,296 integers. Therefore, a four-byte integer can have a value in the range -2^31 = -2,147,483,648 (about - 2 billion) to +2^31 - 1 = +2,147,483,647 (about +2 billion).
All computers store nonnegative integers as binary numbers. Thus, the integer 14,160 has the following representation as a two-byte binary number.
00110111 01010000
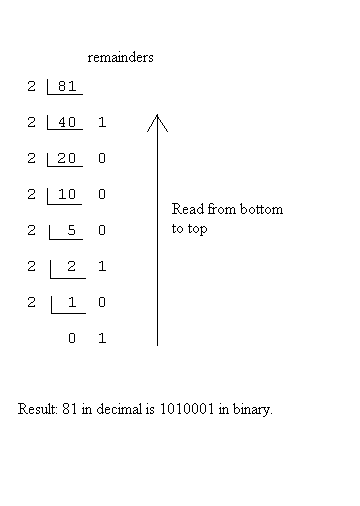
Converting from Decimal to Binary: When we introduced binary numbers, we discussed how to convert a binary number to the equivalent decimal - expand the number using each digit's place value. Given a decimal number, how do we convert it to binary? The method is simple and just requires division by two. At each stage in the example below, the quotient (the result of the division) is written down and the remainder of the division (which must be either 0 or 1 when we divide by 2) is written to the right. The process stops when you reach a quotient of 0.
Example: Following is the conversion of decimal 81 to binary.

Dividing 81 by 2 yields a quotient of 40 and a remainder of 1. Write the remainder to the right. Next divide the previous quotient, 40, by 2. This gives a quotient of 20 and a remainder of 0. This process continues until you get a quotient of 0. To read the result, read the quotients from bottom-to-top.
Binary Arithmetic: Arithmetic is carried out in binary in much the same way as it is carried out in decimal, column-by-column. Just remember that when you add in binary 1 + 1 = 10.
Example: Following is the binary addition 10110 + 10011.
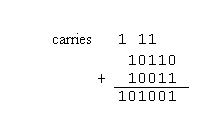
Note that 10110 is 22 in decimal and 10011 is 19 in decimal. The sum, 41, is 101001 in binary.
Overflow: Binary integers are manipulated in the computer's registers, which have a fixed number of bits. (In Burd's text, this is called fixed data format.) Observe in the previous example that we add two 5-bit binaries and obtain a 6-bit binary as the result because of the final carry bit. In a real computer that has, say 32-bit registers, what happens if we add two 32-bit integers and the result is a 33-bit integer (because of a carry, as in the above example.)? The result would be placed into the register with the most significant bit, that is the left-most bit, missing. Thus, the answer in the register would be incorrect! This phenomenon is known as overflow - when the result of an addition is a number with too many bits to fit in the register. Depending on the computer and the program that is controlling the addition, the overflow may or may not be noticed. Thus, when programming integer arithmetic statements the programmer must be aware of the possibility of overflow and take appropriate measures to handle it.
Converting from Decimal to Hexadecimal: When we introduced hexadecimal numbers, we discussed how to convert a hexadecimal number to the equivalent decimal - expand the number using each digit's place value. Given a decimal number, how do we convert it to hexadecimal? The method is straight-forward and requires simple division by 16. This time you must realize that when you divide by 16, the remainder can be an integer from 0 to 15. Also, if you get a remainder in the range 10 to 15, you must write that remainder as the equivalent hexadecimal digit from A to F. The process stops when you reach a quotient of 0. At each stage in the example below, the quotient (the result of the division) is written down and the remainder of the division is written to the right.
Example: Following is the conversion of the decimal 415 to hexadecimal.
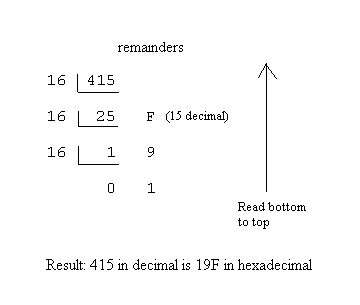
Dividing 415 by 16 yields a quotient of 25 and a remainder of 15, which you must write as the hexadecimal digit F. Write the remainder to the right. Next divide the previous quotient, 25, by 16. This gives a quotient of 1 and a remainder of 9. This process stops at the next step. We obtain a quotient of 0 and a remainder of 1. To read the result, read the quotients from bottom-to-top.
Hexadecimal Arithmetic: Arithmetic can also be carried out in Hexadecimal column-by-column. In this case, however, you must convert all column sums into the equivalent Hexadecimal. For example, if the numbers in the first column are 7 and B (i.e. 11 in decimal), the sum is decimal 18. But you must write the result in hexadecimal as 12 (i.e. 1(16) + 2).
Example: Following is the hexadecimal addition 3A7 + 19B

Note that 3A7 is 935 in decimal ( 3(256) + 10(16) + 7 ) and 19B is 411 in decimal ( 1(256) + 9(16) + 11 ). The sum, 1346, is 542 in hexadecimal.
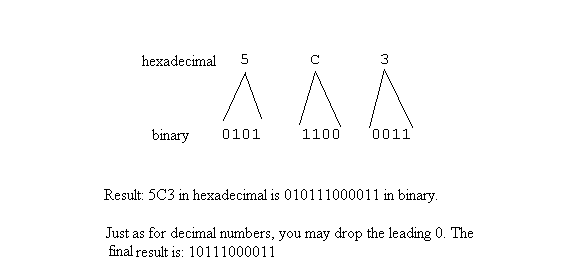
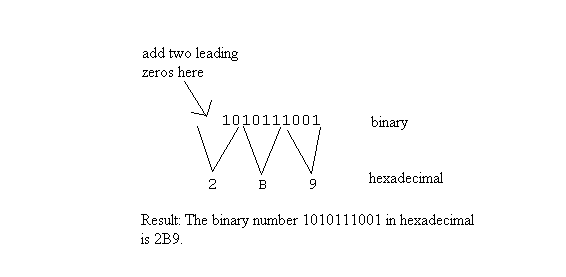
Converting from Binary to Hexadecimal and from Hexadecimal to Binary: The conversion from binary to hexadecimal and the reverse uses the fact discussed in the section on character representation that each hexadecimal digit has a representation by a four-bit binary. See Table 2.
Example: Following is the conversion of hexadecimal 5C3 directly to binary. Using Table 2, convert each hexadecimal digit to the equivalent four-bit binary.
Example: To convert from binary to hexadecimal, reverse the procedure of the preceding example. Using Table 2, convert each group of 4 bits, starting from the right, into the equivalent hexadecimal digit. If the left-most group of bits does not contain 4 bits, then add as many leading zeros as needed to make a group of 4.
Negative Integers: Most computers represent negative integers in 2's complement form, which allows the computer to do binary arithmetic efficiently. Although this may appear to be a strange way to represent negative integers, it is a very efficient way for computers to handle them.
Suppose that we have a computer that represents integers as 8-bit binary numbers - that is the registers of this imaginary computer have 8 bits. To find the 2's complement representation of a negative integer, proceed as follows:
Procedure: To find the 2's complement representation of a binary negative integer:
The resulting binary is the representation of the original negative integer.
Example: What is the 8-bit 2's complement representation of -23?
Following the above procedure:
Thus, -23 as an 8-bit binary in 2's complement form is 11101001
To verify that this is indeed -23, let us add 23 (00010111) and -23 (11101001), which should give us 0.

Note that the extra ninth bit on the left must be discarded because we are assuming that our computer must store integers as 8-bit binaries.
The procedure to find the 2's complement does not depend on the number of bits used to represent the number. Thus, to find the 2's complement of a negative binary, whatever the size of the computer's registers, follows exactly the same procedure .
Exercises:
1. Convert the following decimal numbers to binary:
a) 38 b) 71 c) 142 d) 279
2. Convert the following decimal numbers to hexadecimal:
a) 129 b) 342 c) 417
3. Convert the following binary numbers to hexadecimal:
a) 10001110011 b) 110111011110
4. Convert the following hexadecimal numbers to binary:
a) C1A b) 341 c) FED
5. Add the following binary numbers:
a) 101101101 + 10011011 b) 11010011 + 10001010
6. Add the following hexadecimal numbers:
a) 2AB3 + 35DC b) 1FF9 + F7
7. Assume a computer with 8-bit registers. Find the 2's
complement representation of the following:
a) -1 b) -91
c) -279