Data Representation - Real Numbers

A real number is a number that has a decimal point, such as -73.456 and 0.029854. Most computers store decimal numbers in binary floating-point form. Understanding and working with real numbers in this form is a bit difficult and would take a little more time than we have. We shall, therefore, instead represent real numbers using decimal floating-point form.  The principles of representation are the same whether you use binary or decimal numbers.

To begin, you must understand floating point normal form. To write a number in floating point normal form, move the decimal point to the left of the number's first significant digit (that is, its first nonzero digit) and multiply by an appropriate power of 10. For example,

-73.456 = -.73456 x 10^2

The power of 10 is 2 because we moved the decimal point left two places to put it to the left of the digit 7. Also,

0.029854 = .29854 x 10^-1

The power of 10 is -1 because we moved the decimal point right one place to put it to the left of the digit 2.

The decimal part of a number in normal floating point form is the number's mantissa and the power of 10 is the number's exponent.

Recall from the discussion on integer representation, that the number of bits used to store an integer in a real computer is fixed, usually by the number of bits in a register. Floating-point numbers are also manipulated in registers - floating-point registers - and are thus represented by a fixed number of bits. Because we are going to represent floating-point numbers in decimal, we shall assume a fixed number of digits in writing a floating-point number. It is also important to observe the three things necessary to store are the sign of the number, the digits and the exponent. The decimal point is understood to be to the left of the first digit of the mantissa, and the base for the exponent is understood to be 10. This fact is reflected in how we shall represent floating-point numbers in the next section.

8-digit Excess-50 Floating-Point Notation:  In our imaginary computer, we will assume that a floating-point number must be stored as an 8-decimal-digit number. The number will be in three parts. The first digit will represent the sign of the mantissa. The second part, consisting of the next two digits, will represent the exponent. The third part, consisting of the last five digits, will represent the digits of the mantissa.

                                                    S EE MMMMM

Thus, the eight digits, 05337826, will represent an 8-digit excess-50 floating point number.

Now, let's discuss details of the three parts of such a number. The first digit represents the sign. We will (and this is quite arbitrary; another scheme would work just as well) use 0 to represent a plus + and 1 to represent a minus -.

The exponent part is a little more involved. As we saw in the examples of floating-point normal form, the exponent of a number in that form can be negative. How can we use the two digits for the exponent to represent the exponent and the sign? There are several ways to do that. The way we shall use is called excess-50 notation (This is similar to the technique actually used to represent floating-point number exponents in a real computer.) The number we will use to store the exponent will be 50 more than the exponent itself - that is, it is 50 in excess of the actual exponent. Thus, in the above example, 05337826, the exponent part of 53 actually represents an exponent of 53 - 50 = 3. This is done so that we can represent negative exponents as well. For example, an exponent part of 48 would represent an exponent of 48 - 50 = -2.

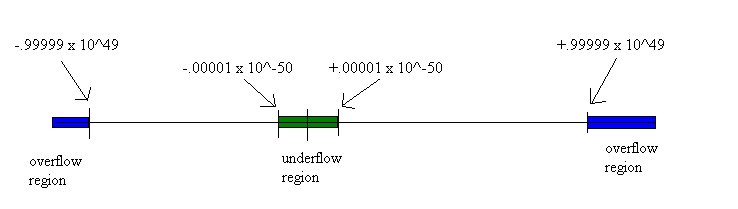
Note that the largest exponent that we can represent is 49 (99 - 50); and the smallest exponent we can represent is -50 (0 -50).

Finally, the last five digits represent the mantissa of the number, with the decimal point to the left of the first digit.

Example: What number does 05337826 represent?

The sign, 0, means that the number is positive. The exponent part of 53 means that the exponent is 53 - 50 = 3, and the mantissa is .37826. Thus, the number is

                 +.37826 x 10^3  =  +378.26

Example: What number does 04793516 represent?

The sign is 0, or +. The exponent part of 47 means that the exponent is 47 - 50 = -3. The mantissa is .93516. Thus the number is

                 +.93516 x 10^-3  = +.00093516

Example: Write -4.0231457 in 8-digit excess-50 notation.

First, put the number in normal floating-point form.

               -4.0231457 = -.40231457 x 10^1

The number is negative, so the sign will be 1. To get the exponent part, add 50 to the exponent of the number in normal form. The exponent is 1. Therefore, the exponent part will be 1 + 50 = 51. The mantissa of the given number has 8 digits. We must get rid of three digits because our format allows only 5 digits in the mantissa. Thus, we truncate (or chop off) the last three digits of the mantissa, giving 40231 as the digits of the mantissa.

The number in 8-digit excess-50 format is, therefore, 15140231.

Example: Write the number +.00625 in 8-digit excess-50 notation.

First, put the number in normal floating-point form.

                +.00625 = +.625 x 10^-2

The number is positive, so the sign part will be 0. To get the exponent part, add 50 to the exponent of the number in normal form. The exponent in normal form is -2. Therefore, the exponent part will be -2 + 50 = 48. The mantissa of the given number has only three digits. We must now add two digits because the mantissa of a number in our format MUST have exactly five digits. To do this, we simply append two zeros to the three digits, giving 62500 as the mantissa.

The number in 8-digit excess-50 format is, therefore, 04862500.

Real Number Arithmetic: We shall not discuss real-number arithmetic because it would take us too far from the main topics of the course. Addition and subtraction are complicated by the fact that you have to "align" the decimal points before doing the arithmetic, just as you do when adding and subtracting decimal numbers by hand. Multiplication and division are simpler than addition and subtraction.

What you should keep in mind is that when doing real number arithmetic, it is possible to have overflow. This would occur when the resulting exponent is too large to represent (larger than 49). It is also possible when doing real number arithmetic to have underflow - the number is a decimal magnitude too small to represent. Thus, its exponent would be smaller than -50.

Exercises:

1. Put the following numbers into floating-point normal form.
    a) 4901.229     b) -.00074652      c) +1245

2. Write each of the numbers in Exercise 1 in 8-digit
    excess-50 form.

3. Write the following 8-digit excess-50 numbers in decimal
    form.
    a) 04431415     b) 15574819      c) 05428931