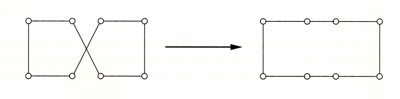
Assume we have all interpoint distances between n cities, giving a search space of (n - 1)! different tours. What is a good notion of neighborhood? The most obvious notion is to consider two tours as being close if they differ in just a few edges. They can't differ in just one edge, so we will consider differences that can be obtained by removing two edges of s and then putting in two other edges. Here's an example of a local move: