In the example on the previous page, each run of local search has a reasonable chance of finding the global optimum. This isn't always true. As the problem size grows, the ratio of bad to good local optima often increases, sometimes to the point of being exponentially large. In such cases, simply repeating the local search a few times is ineffective.

A different avenue of attack is to occasionally allow moves that actually increase the cost, in the hope that they will pull the search out of dead ends. The method of simulated annealing redefines the local search by introducing the notion of a temperature T.

If T is zero, this is identical to our previous local search. But if T is large, then moves that increase the cost are occasionally accepted. What value of T should be used?

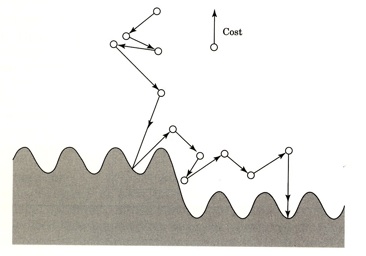
The trick is to start with T large and then gradually reduce it to zero. Thus initially, the local search can wander around quite freely, with only a mild preference for low-cost solutions. As time goes on, this preference becomes stronger, and the system mostly sticks to the lower-cost region of the search space, with occasional excursions out of it to escape local optima. Eventually, when the temperature drops further, the system converges on a solution. The figure below shows this process schematically.

Simulated annealing is inspired by the physics of crystallization. When a substance is to be crystallized, it starts in liquid state, with its particles in relatively unconstrained motion. Then it is slowly cooled, and as this happens, the particles gradually settle into their crystal lattice.