


The problem of graph partitioning arises in a diversity of applications, from circuit layout to program analysis to image segmentation. The Graph Partitioning task is specified by:
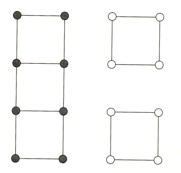
Input: An undirected graph G = (V, E) with nonnegative edge weights; a real number m between 0 and 1/2. Output: A partition of the vertices into two groups A and B, each of size at least m * |V|. Goal: Minimize the capacity of the cut (A, B). The figure below shows an example in which the graph has 16 nodes, all edge weights are 0 or 1, and the optimal solution has cost 0.
An instance of the Graph Partitioning task, with the optimal partition for m = 1/2. Vertices on one side of the cut are shaded.