In designing a local search algorithm, it will be a big convenience to focus on the special case m = 1/2, in which A and B are forced to contain exactly half the vertices. The apparent loss of generality is purely cosmetic, as GRAPH PARTITIONING reduces to this particular case.

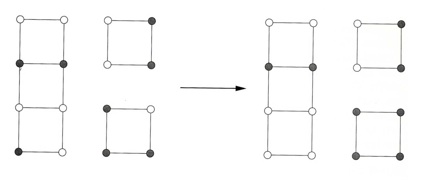
We need to decide upon a neighborhood structure for our problem, and there is one obvious way to do this. Let (A, B), with |A| = |B|, be a candidate solution; we will define its neighbors to be all solutions obtainable by swapping one pair of vertices across the cut, that is, all solutions of the form (A - {a} + {b}, B - {b} + {a}) where a is in A and b is in B. Here's an example of a local move: